华东师大版八年级数学下册课件:19.1.1矩形的性质(共25张PPT)
文档属性
| 名称 | 华东师大版八年级数学下册课件:19.1.1矩形的性质(共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-16 19:52:46 | ||
图片预览






文档简介
(共25张PPT)
第19章
矩形、菱形与正方形
19.1
矩形
1.矩形的性质
八年级下册
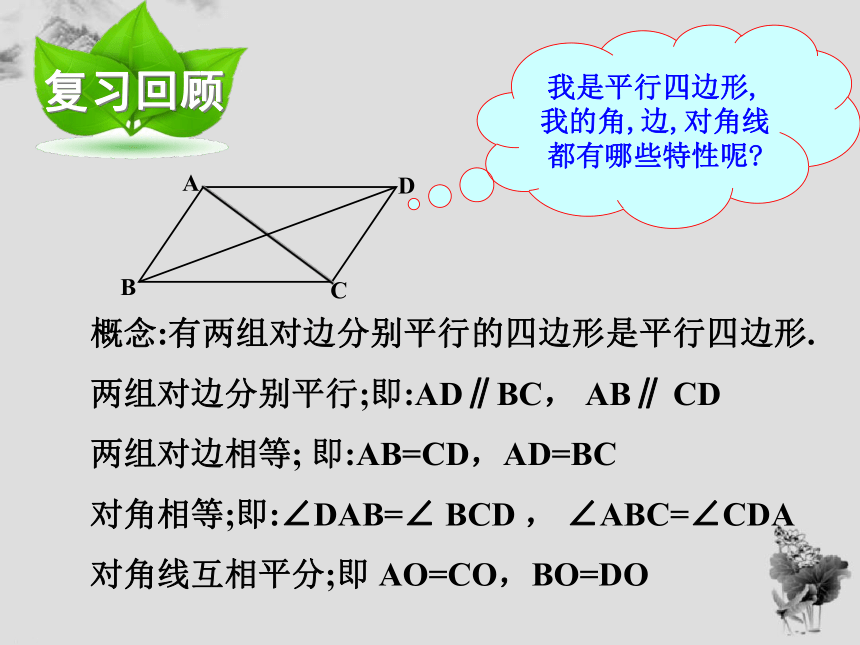
我是平行四边形,我的角,边,对角线都有哪些特性呢?
概念:有两组对边分别平行的四边形是平行四边形.
两组对边分别平行;即:AD∥BC,
AB∥
CD
两组对边相等;
即:AB=CD,AD=BC
对角相等;即:∠DAB=∠
BCD
,
∠ABC=∠CDA
对角线互相平分;即
AO=CO,BO=DO
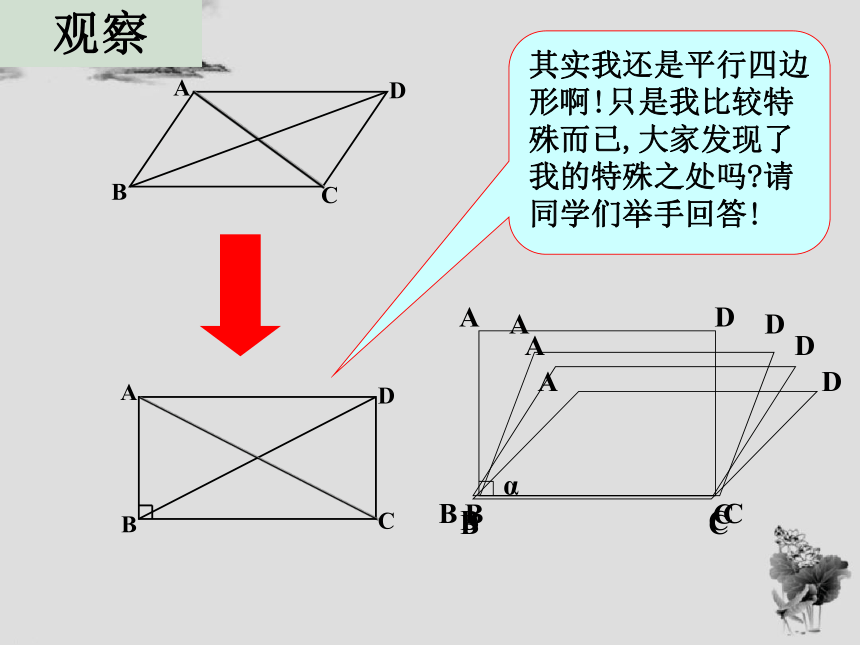
观察下面图案,有没有你熟悉的几何图形?
其实我还是平行四边形啊!只是我比较特殊而已,大家发现了我的特殊之处吗?请同学们举手回答!
观察
矩形:
木门
纸张
电脑显示器
有一个角是直角的特殊平行四边形。
实质上:
矩形是特殊的平行四边形。
特殊
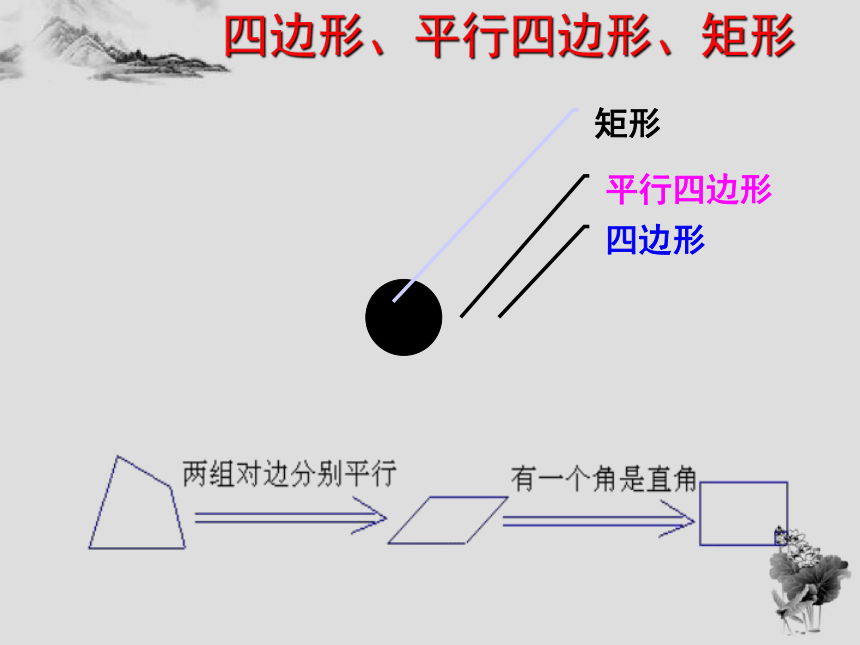
四边形、平行四边形、矩形
探究
问题一:矩形是特殊的平行四边形,它是否具有平行四边形的一切性质?若是,请你说出这些性质.
问题二:矩形既然是特殊的平行四边形,它有没有特殊的性质?请同学们画出任意一个矩形ABCD,从对称性、边、角、对角线等方面探索它的性质.
矩形的性质
探究
问题三:你能证明矩形的特有性质吗?
说明:矩形的四个角都是直角可借助平行四边形的对角相等及矩形的定义证.
矩形的对角线相等可利用平行四边形的对角线互相平分,利用三角形全等证.
想一想:
矩形是轴对称图形吗?是中心对称图形吗?
对称轴有几条?
是
是
两条
矩形几何特征
矩形特征1:
矩形的四个角都是直角
在矩形ABCD,
∠ABC=∠BCD=∠CDA=
∠BAD=90°
矩形特征2:矩形的对角线相等且互相平分.
∵AC,BD是矩形ABCD的对角线
∴AC=BD,OA=OC,OB=OD
邻边:互相垂直
四个角都是直角
互相平分
相等
(1)边:
(2)角:
(3)对角线:
(共性)
(共性)
(个性)
(个性)
(个性)
(共性)
O
矩形特征
概括
矩形的性质:
(1)矩形具有平行四边形的所有性质;
(2)矩形的四个角都是直角;
(3)矩形的对角线相等;
(4)矩形既是中心对称图形,又是轴对称
图形,对称轴有两条.
练习
矩形的定义中有两个条件:一是
,二
是
.
有一个角是直角
四边形是平行四边形
判断:
(1)有一个角是直角的四边形是矩形.
(
)
(2)矩形的对角线互相平分.
(
)
×
√
练习
下列性质中,矩形不一定具有的是(
)
A.对角线相等
B.四个角都相等
C.对角线互相垂直
D.是轴对称图形
C
矩形具有而平行四边形不具有的性质是(
)
A.对边平行
B.对角相等
C.对角线互相平分
D.对角线相等
D
练习
如图,矩形ABCD的两条对角线相交于点O,∠AOD=120°.求证:AC=2AB.
证明:∵∠AOD=120°,∴∠COD=60°.
又∵四边形ABCD是矩形,
∴OD=OC,∴△ODC是等边三角形.
∴AC=2AB.
在直角三角形中,30°角所对的直角边等于斜边的一半.
例1
如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形周长的和是86
cm,矩形的对角线长是13
cm,那么该矩形的周长是多少?
练习:
已知:矩形ABCD的两条对角线相交于点0,
∠AOD=120°,
AB=4cm,
求矩形对角线的长.
解:∵四边形ABCD是矩形
∴AC
=
BD(
)
矩形的对角线相等
∴OA
=
OB
平行四边形的对角线互相平分
∵∠AOD
=120°
∴∠AOB
=180°-∠AOD
=
60°
∴△AOB
是等边三角形
∴OA
=
OB
=
AB
=
4cm
∴AC
=
2OA
=
8cm.
例2
例2如图,在矩形
ABCD中,AB=3,BC=4,BE⊥AC于点E.试求BE的长.
例3
例3如图,在矩形
ABCD中,对角线AC与BD相交于点O,AE垂直平分线段BO,垂足为点E,BD=15
cm.求AC、AB的长.
矩形ABCD的周长为56cm,对角线AC、BD交于O,
△BOC和△AOB的周长差是4cm,那么矩形各边的
长是多少?
练习
如图,在矩形
ABCD中,对角线AC与BD相交于点O,∠AOB=60°,AB=3.6.求AC与AD的长.(精确到0.1)
∴AB=CD,AD=BC(平行四边形的
).
AO=CO,BO=DO(平行四边形的
).
解:∵AB+BC+CD+DA
=
56,
(BC+BO+CO)-(AB+AO+BO)=
4,
又∵四边形ABCD是矩形,
∴
AB
+
BC
=28,BC-AB
=
4,
∴
AD
=
BC
=16,AB=CD
=12.
对边相等
对角线互相平分
通过这节课的学习,你有哪些收获?
1.从教材习题中选取,
2.完成练习册本课时的习题.
第19章
矩形、菱形与正方形
19.1
矩形
1.矩形的性质
八年级下册
我是平行四边形,我的角,边,对角线都有哪些特性呢?
概念:有两组对边分别平行的四边形是平行四边形.
两组对边分别平行;即:AD∥BC,
AB∥
CD
两组对边相等;
即:AB=CD,AD=BC
对角相等;即:∠DAB=∠
BCD
,
∠ABC=∠CDA
对角线互相平分;即
AO=CO,BO=DO
观察下面图案,有没有你熟悉的几何图形?
其实我还是平行四边形啊!只是我比较特殊而已,大家发现了我的特殊之处吗?请同学们举手回答!
观察
矩形:
木门
纸张
电脑显示器
有一个角是直角的特殊平行四边形。
实质上:
矩形是特殊的平行四边形。
特殊
四边形、平行四边形、矩形
探究
问题一:矩形是特殊的平行四边形,它是否具有平行四边形的一切性质?若是,请你说出这些性质.
问题二:矩形既然是特殊的平行四边形,它有没有特殊的性质?请同学们画出任意一个矩形ABCD,从对称性、边、角、对角线等方面探索它的性质.
矩形的性质
探究
问题三:你能证明矩形的特有性质吗?
说明:矩形的四个角都是直角可借助平行四边形的对角相等及矩形的定义证.
矩形的对角线相等可利用平行四边形的对角线互相平分,利用三角形全等证.
想一想:
矩形是轴对称图形吗?是中心对称图形吗?
对称轴有几条?
是
是
两条
矩形几何特征
矩形特征1:
矩形的四个角都是直角
在矩形ABCD,
∠ABC=∠BCD=∠CDA=
∠BAD=90°
矩形特征2:矩形的对角线相等且互相平分.
∵AC,BD是矩形ABCD的对角线
∴AC=BD,OA=OC,OB=OD
邻边:互相垂直
四个角都是直角
互相平分
相等
(1)边:
(2)角:
(3)对角线:
(共性)
(共性)
(个性)
(个性)
(个性)
(共性)
O
矩形特征
概括
矩形的性质:
(1)矩形具有平行四边形的所有性质;
(2)矩形的四个角都是直角;
(3)矩形的对角线相等;
(4)矩形既是中心对称图形,又是轴对称
图形,对称轴有两条.
练习
矩形的定义中有两个条件:一是
,二
是
.
有一个角是直角
四边形是平行四边形
判断:
(1)有一个角是直角的四边形是矩形.
(
)
(2)矩形的对角线互相平分.
(
)
×
√
练习
下列性质中,矩形不一定具有的是(
)
A.对角线相等
B.四个角都相等
C.对角线互相垂直
D.是轴对称图形
C
矩形具有而平行四边形不具有的性质是(
)
A.对边平行
B.对角相等
C.对角线互相平分
D.对角线相等
D
练习
如图,矩形ABCD的两条对角线相交于点O,∠AOD=120°.求证:AC=2AB.
证明:∵∠AOD=120°,∴∠COD=60°.
又∵四边形ABCD是矩形,
∴OD=OC,∴△ODC是等边三角形.
∴AC=2AB.
在直角三角形中,30°角所对的直角边等于斜边的一半.
例1
如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形周长的和是86
cm,矩形的对角线长是13
cm,那么该矩形的周长是多少?
练习:
已知:矩形ABCD的两条对角线相交于点0,
∠AOD=120°,
AB=4cm,
求矩形对角线的长.
解:∵四边形ABCD是矩形
∴AC
=
BD(
)
矩形的对角线相等
∴OA
=
OB
平行四边形的对角线互相平分
∵∠AOD
=120°
∴∠AOB
=180°-∠AOD
=
60°
∴△AOB
是等边三角形
∴OA
=
OB
=
AB
=
4cm
∴AC
=
2OA
=
8cm.
例2
例2如图,在矩形
ABCD中,AB=3,BC=4,BE⊥AC于点E.试求BE的长.
例3
例3如图,在矩形
ABCD中,对角线AC与BD相交于点O,AE垂直平分线段BO,垂足为点E,BD=15
cm.求AC、AB的长.
矩形ABCD的周长为56cm,对角线AC、BD交于O,
△BOC和△AOB的周长差是4cm,那么矩形各边的
长是多少?
练习
如图,在矩形
ABCD中,对角线AC与BD相交于点O,∠AOB=60°,AB=3.6.求AC与AD的长.(精确到0.1)
∴AB=CD,AD=BC(平行四边形的
).
AO=CO,BO=DO(平行四边形的
).
解:∵AB+BC+CD+DA
=
56,
(BC+BO+CO)-(AB+AO+BO)=
4,
又∵四边形ABCD是矩形,
∴
AB
+
BC
=28,BC-AB
=
4,
∴
AD
=
BC
=16,AB=CD
=12.
对边相等
对角线互相平分
通过这节课的学习,你有哪些收获?
1.从教材习题中选取,
2.完成练习册本课时的习题.
