华东师大版八年级数学下册课件:19.1.2矩形的判定(共22张PPT)
文档属性
| 名称 | 华东师大版八年级数学下册课件:19.1.2矩形的判定(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-16 00:00:00 | ||
图片预览



文档简介
(共22张PPT)
第19章
矩形、菱形与正方形
19.1
矩形
2.矩形的判定
八年级下册
一个角是直角
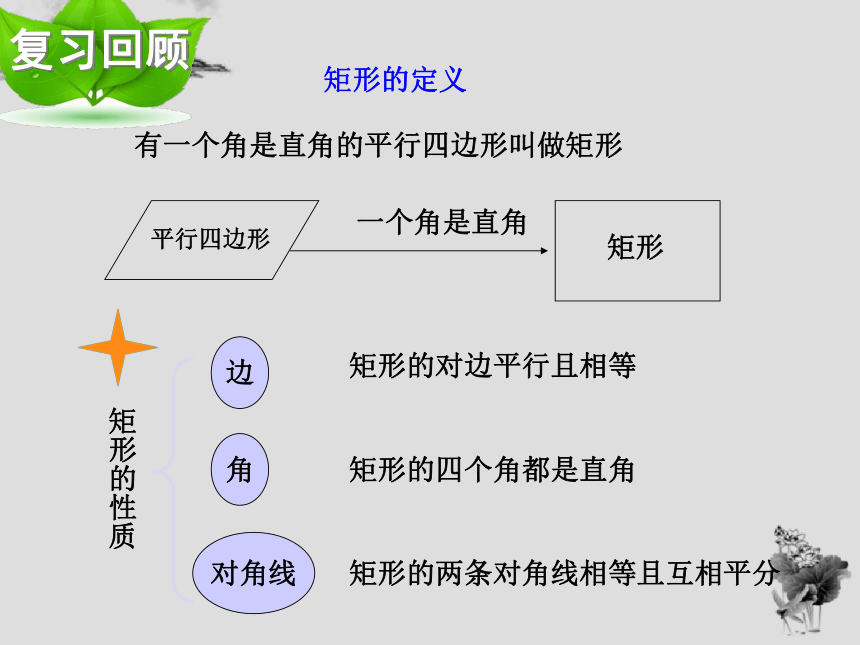
有一个角是直角的平行四边形叫做矩形
矩形的两条对角线相等且互相平分
矩形的对边平行且相等
矩形的四个角都是直角
边
对角线
角
矩形的定义
矩形的性质
思考
(1)平行四边形的判定方法除定义外,还有哪几种判定方法?
(2)这些判定方法是通过什么方法得到的?
(平行四边形性质定理的逆命题,猜测、验证、逻辑推理得到的)
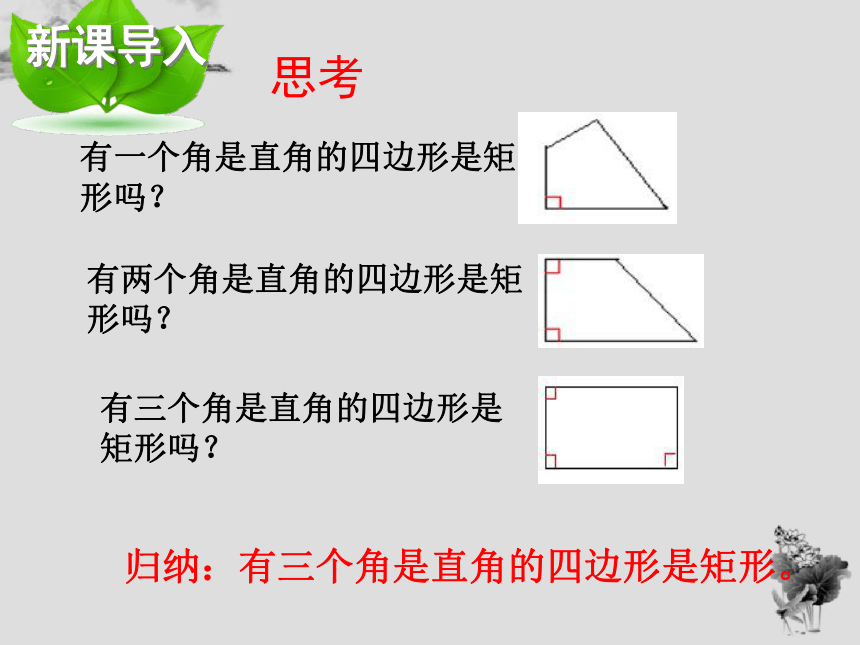
归纳:有三个角是直角的四边形是矩形。
有一个角是直角的四边形是矩形吗?
有两个角是直角的四边形是矩形吗?
有三个角是直角的四边形是矩形吗?
思考
验证
观察你所作的图形,它是一个矩形吗?
如图,作一个三个角都是直角的四边形.
步骤:
1.任意作两条互相垂直
的线段AB、AD;
2.过点B作垂直于AB的
直线l;
3.过点D作垂直于AD的直线m,交l于点C,即得一个三个角都是直角的四边形ABCD.
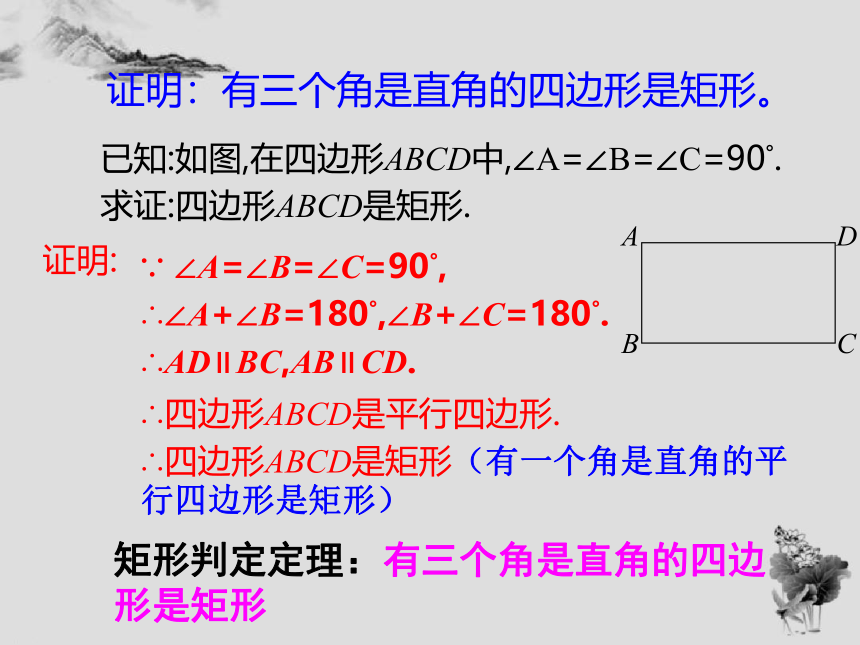
证明:有三个角是直角的四边形是矩形。
已知:如图,在四边形ABCD中,∠A=∠B=∠C=90°.
证明:
∵
∠A=∠B=∠C=90°,
∴∠A+∠B=180°,∠B+∠C=180°.
∴AD∥BC,AB∥CD.
求证:四边形ABCD是矩形.
∴四边形ABCD是平行四边形.
∴四边形ABCD是矩形(有一个角是直角的平行四边形是矩形)
矩形判定定理:有三个角是直角的四边形是矩形
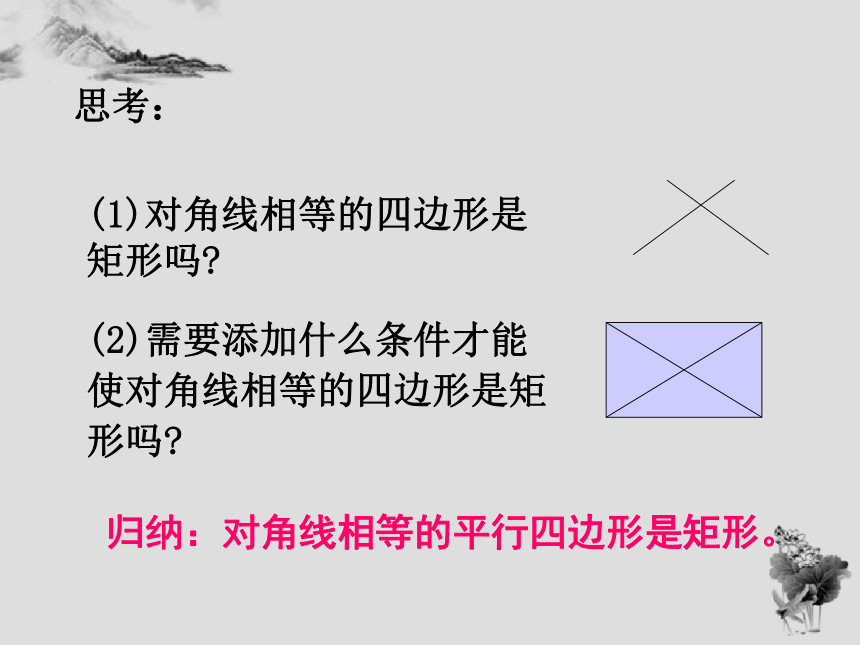
思考:
(1)对角线相等的四边形是矩形吗?
(2)需要添加什么条件才能使对角线相等的四边形是矩形吗?
归纳:对角线相等的平行四边形是矩形。
验证
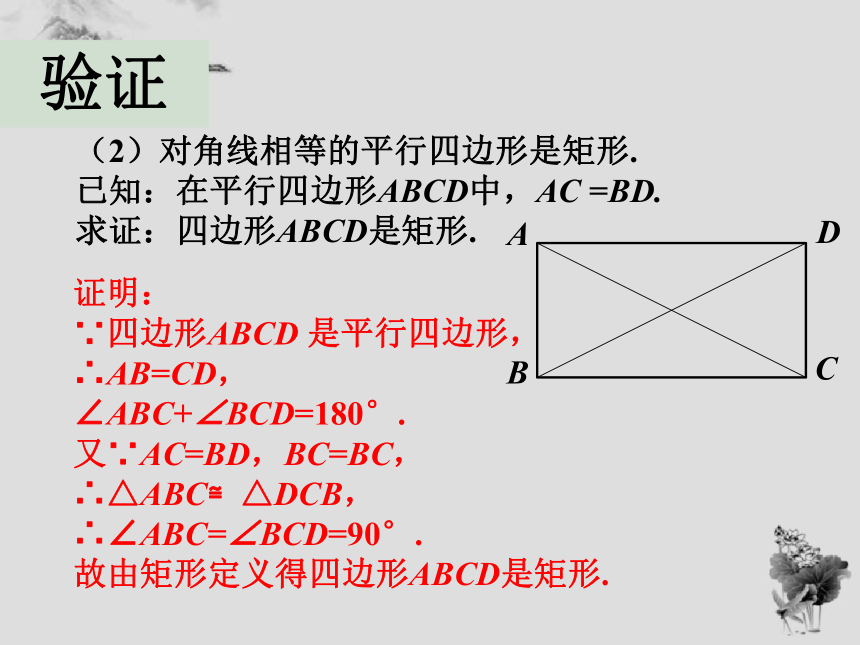
(2)对角线相等的平行四边形是矩形.
已知:在平行四边形ABCD中,AC
=BD.
求证:四边形ABCD是矩形.
证明:
∵四边形ABCD
是平行四边形,
∴AB=CD,
∠ABC+∠BCD=180°.
又∵AC=BD,BC=BC,
∴△ABC≌△DCB,∴∠ABC=∠BCD=90°.
故由矩形定义得四边形ABCD是矩形.
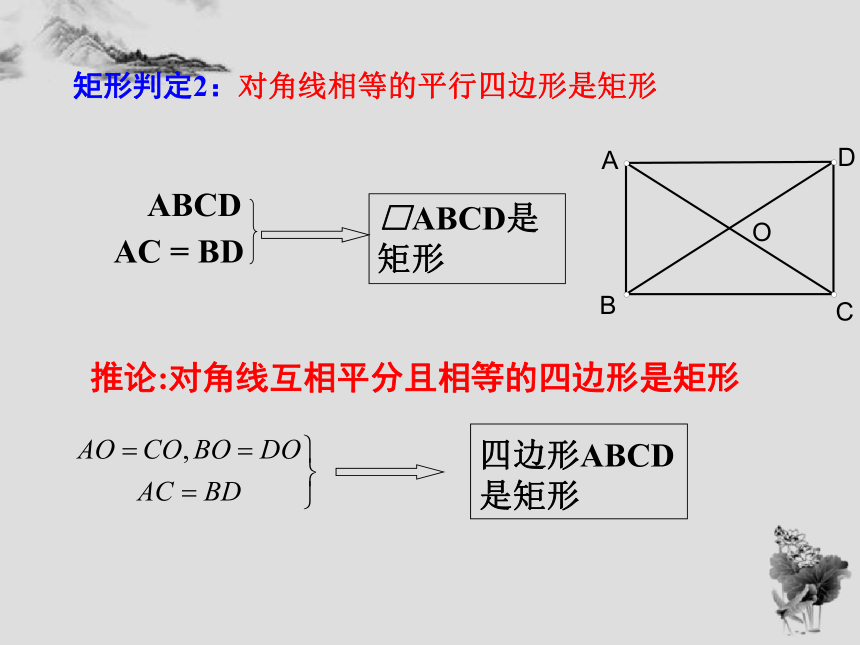
矩形判定2:对角线相等的平行四边形是矩形
□ABCD是矩形
推论:对角线互相平分且相等的四边形是矩形
四边形ABCD
是矩形
问题:木工师傅检查所做的门窗是否是矩形常用什么方法?为什么?
答:木工师傅靠测量门窗的对角线是否相等来判断所做的门窗是否是矩形。因为对角线相等的平行四边形是矩形。
例1如图,点O是矩形ABCD的对角线AC与BD的交点,E、F、G、H分别是AO、BO、CO、DO上的一点,且AE=BF=CG=DH.求证:四边形EFGH是矩形.
例1
例2如图,四边形ABCD是由两个全等的正三角形ABD和BCD组成的,M、N分别为BC、AD的中点.求证:四边形BMDN是矩形.
例2
判断对错
⒈对角线相等的四边形是矩形(
)
⒉对角线互相平分且相等的四边形是矩形(
)
⒊有一个角是直角的四边形是矩形(
)
⒋有四个角是直角的四边形是矩形(
)
⒌四个角都相等的四边形是矩形(
)
⒍对角线相等,且有一个角是直角的四边形是矩形(
)
⒎一组邻边垂直,一组对边平行且相等的四边形是矩形
(
)
⒏对角线相等且互相垂直的四边形是矩形(
)
√
√
√
√
×
×
×
×
2.已知:如图四边形ABCD中AB⊥BC,AD∥BC,AD=BC,试说明四边形ABCD是矩形。
解:∵
AD=CB,AD∥CB
∴四边形ABCD是平行四边形
∵AB⊥BC
∴∠B=90°
∴
□
ABCD是矩形
3.已知M为
ABCD的AD边的中点,且MB=MC。
求证:
ABCD是矩形。
证明:
∵ABCD是平行四边形
AB=DC
∵M是AD的中点
∴AM=DM
∵MB=MC
∴△BAM≌
△CDM
∴∠A=∠D
∴∠A+
∠D=1800
∴∠A=
900
4如图,AB、CD是⊙O的两条直径,四边形ACBD是矩形吗?请证明你的结论.
练习
5如图,在平行四边形ABCD中,∠1=∠2.此时,四边形ABCD是矩形吗?为什么?
练习
练习
6如图,平行四边形ABCD的四个内角的平分线分别相交于点E、F、G、H.求证:四边形EFGH是矩形.
练习
有一个角是直角
对角线相等
有三个角是直角
平行四边形
矩形
四边形
任意一个四边形,
三角直角定矩形。
对于平行四边形,
一个直角即可定;
对线相等也矩形。
矩形的判定口诀:
1.从教材习题中选取,
2.完成练习册本课时的习题.
第19章
矩形、菱形与正方形
19.1
矩形
2.矩形的判定
八年级下册
一个角是直角
有一个角是直角的平行四边形叫做矩形
矩形的两条对角线相等且互相平分
矩形的对边平行且相等
矩形的四个角都是直角
边
对角线
角
矩形的定义
矩形的性质
思考
(1)平行四边形的判定方法除定义外,还有哪几种判定方法?
(2)这些判定方法是通过什么方法得到的?
(平行四边形性质定理的逆命题,猜测、验证、逻辑推理得到的)
归纳:有三个角是直角的四边形是矩形。
有一个角是直角的四边形是矩形吗?
有两个角是直角的四边形是矩形吗?
有三个角是直角的四边形是矩形吗?
思考
验证
观察你所作的图形,它是一个矩形吗?
如图,作一个三个角都是直角的四边形.
步骤:
1.任意作两条互相垂直
的线段AB、AD;
2.过点B作垂直于AB的
直线l;
3.过点D作垂直于AD的直线m,交l于点C,即得一个三个角都是直角的四边形ABCD.
证明:有三个角是直角的四边形是矩形。
已知:如图,在四边形ABCD中,∠A=∠B=∠C=90°.
证明:
∵
∠A=∠B=∠C=90°,
∴∠A+∠B=180°,∠B+∠C=180°.
∴AD∥BC,AB∥CD.
求证:四边形ABCD是矩形.
∴四边形ABCD是平行四边形.
∴四边形ABCD是矩形(有一个角是直角的平行四边形是矩形)
矩形判定定理:有三个角是直角的四边形是矩形
思考:
(1)对角线相等的四边形是矩形吗?
(2)需要添加什么条件才能使对角线相等的四边形是矩形吗?
归纳:对角线相等的平行四边形是矩形。
验证
(2)对角线相等的平行四边形是矩形.
已知:在平行四边形ABCD中,AC
=BD.
求证:四边形ABCD是矩形.
证明:
∵四边形ABCD
是平行四边形,
∴AB=CD,
∠ABC+∠BCD=180°.
又∵AC=BD,BC=BC,
∴△ABC≌△DCB,∴∠ABC=∠BCD=90°.
故由矩形定义得四边形ABCD是矩形.
矩形判定2:对角线相等的平行四边形是矩形
□ABCD是矩形
推论:对角线互相平分且相等的四边形是矩形
四边形ABCD
是矩形
问题:木工师傅检查所做的门窗是否是矩形常用什么方法?为什么?
答:木工师傅靠测量门窗的对角线是否相等来判断所做的门窗是否是矩形。因为对角线相等的平行四边形是矩形。
例1如图,点O是矩形ABCD的对角线AC与BD的交点,E、F、G、H分别是AO、BO、CO、DO上的一点,且AE=BF=CG=DH.求证:四边形EFGH是矩形.
例1
例2如图,四边形ABCD是由两个全等的正三角形ABD和BCD组成的,M、N分别为BC、AD的中点.求证:四边形BMDN是矩形.
例2
判断对错
⒈对角线相等的四边形是矩形(
)
⒉对角线互相平分且相等的四边形是矩形(
)
⒊有一个角是直角的四边形是矩形(
)
⒋有四个角是直角的四边形是矩形(
)
⒌四个角都相等的四边形是矩形(
)
⒍对角线相等,且有一个角是直角的四边形是矩形(
)
⒎一组邻边垂直,一组对边平行且相等的四边形是矩形
(
)
⒏对角线相等且互相垂直的四边形是矩形(
)
√
√
√
√
×
×
×
×
2.已知:如图四边形ABCD中AB⊥BC,AD∥BC,AD=BC,试说明四边形ABCD是矩形。
解:∵
AD=CB,AD∥CB
∴四边形ABCD是平行四边形
∵AB⊥BC
∴∠B=90°
∴
□
ABCD是矩形
3.已知M为
ABCD的AD边的中点,且MB=MC。
求证:
ABCD是矩形。
证明:
∵ABCD是平行四边形
AB=DC
∵M是AD的中点
∴AM=DM
∵MB=MC
∴△BAM≌
△CDM
∴∠A=∠D
∴∠A+
∠D=1800
∴∠A=
900
4如图,AB、CD是⊙O的两条直径,四边形ACBD是矩形吗?请证明你的结论.
练习
5如图,在平行四边形ABCD中,∠1=∠2.此时,四边形ABCD是矩形吗?为什么?
练习
练习
6如图,平行四边形ABCD的四个内角的平分线分别相交于点E、F、G、H.求证:四边形EFGH是矩形.
练习
有一个角是直角
对角线相等
有三个角是直角
平行四边形
矩形
四边形
任意一个四边形,
三角直角定矩形。
对于平行四边形,
一个直角即可定;
对线相等也矩形。
矩形的判定口诀:
1.从教材习题中选取,
2.完成练习册本课时的习题.
