苏科版七下数学 7.3图形的平移 教案
文档属性
| 名称 | 苏科版七下数学 7.3图形的平移 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 152.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-17 08:03:08 | ||
图片预览


文档简介
7.3
图形的平移
教学目标:
1.认识平移的概念及平移的不变性,理解平移图形中对应线段平行且相等的性质;2.能按要求作出简单平面图形平移后的图形,能用平移的性质解决实际问题.
教学重点:
理解图形平移的基本性质,并能按要求作出简单平面图形平移后的图形.
教学难点:
能运用平移的性质解决实际问题.
教学过程(教师)
新课引入——情景导入:请你判断
小明跟着妈妈乘观光电梯上楼,一会儿,小明兴奋地大叫起来:“妈妈!妈妈!你看我长高了!我比对面的大楼还要高!”小明说的对吗?为什么??
接触平移现象:教师通过多媒体展示(画面)现实生活中平移的具体实例,你还能举出生活中类似的例子吗?根据上述一些现象,你能说明什么样的图形运动称为平移?
辨一辨、议一议:在以下现象中,属于平移的是
(
)
①
在荡秋千的小朋友;②
打气筒打气时,活塞的运动;③
钟摆的摆动;④
传送带上,瓶装饮料的移动.A.①②
B.①③
C.②③
D.②④
例1
如图,4个小三角形都是等边三角形,边长为1.3cm.你能通过平移△ABC得到其他三角形吗?若能,请画出平移方向,并说出平移的距离.
活动探究:把图中的三角形ABC(可记为△ABC)向右平移6个格子,画出所得的△A′B′C′.度量△ABC与△A′B′C′的边、角的大小,你发现什么了呢?你认为图形平移具有什么特征呢?
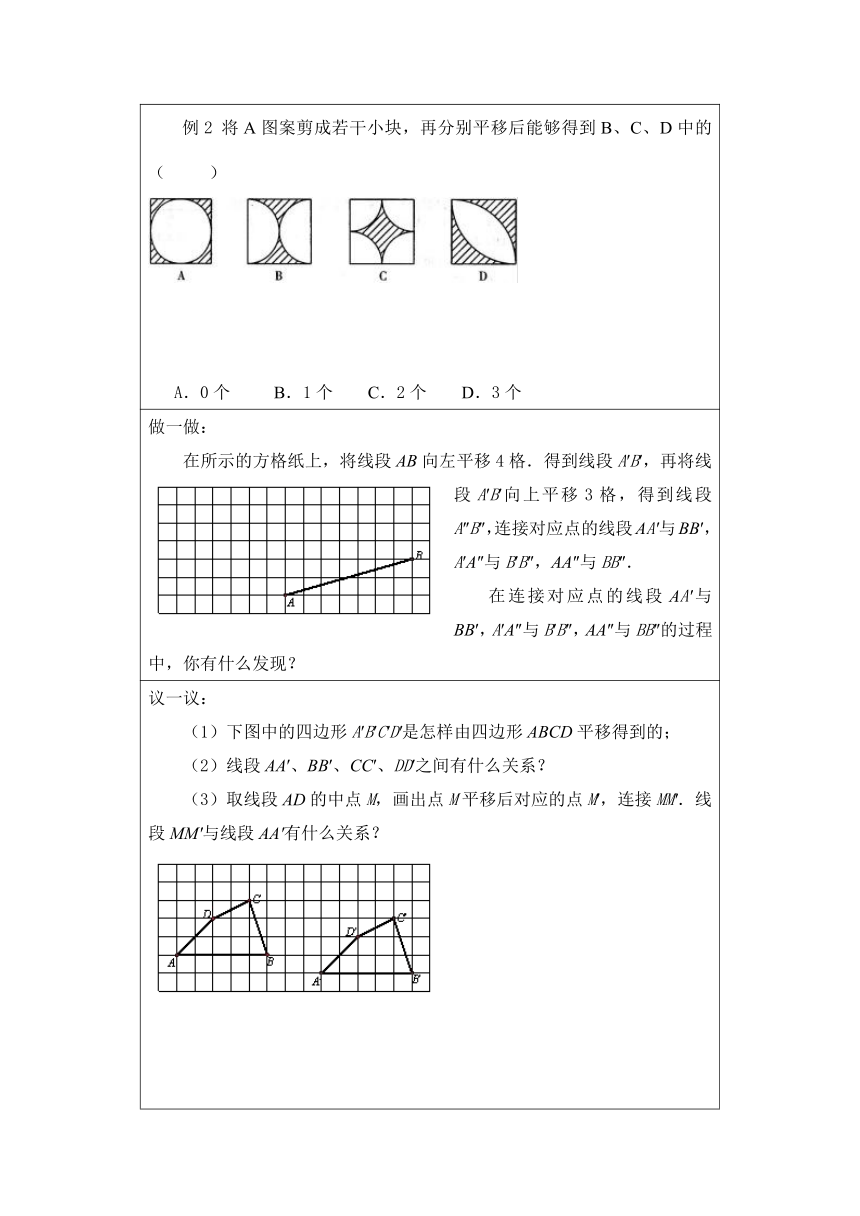
例2
将A图案剪成若干小块,再分别平移后能够得到B、C、D中的
(
)
A.0个
B.1个
C.2个
D.3个
做一做:在所示的方格纸上,将线段AB向左平移4格.得到线段A′B′,再将线段A′B′向上平移3格,得到线段A″B″,连接对应点的线段AA′与BB′,A′A″与B′B″,AA″与BB″.在连接对应点的线段AA′与BB′,A′A″与B′B″,AA″与BB″的过程中,你有什么发现?
议一议:(1)下图中的四边形A′B′C′D′是怎样由四边形ABCD平移得到的;(2)线段AA′、BB′、CC′、DD′之间有什么关系?(3)取线段AD的中点M,画出点M平移后对应的点M′,连接MM′.线段MM′与线段AA′有什么关系?你能否用一句话来概括这种关系?
例3 已知△ABC和点D,平移△ABC,使△ABC的顶点A移动到了点D的位置.
课堂反馈:1.在下面的六幅图案中,(2)、(3)、(4)、(5)、(6)中的哪个图案可以通过平移图案(1)得到?2.如图,四边形EFGH是由四边形ABCD平移得到的,已知AD=5,∠B=70°,则?(
)A.FG=5,∠G=70°B.EH=5,∠F=70°C.EF=5,∠F=70°D.EF=5,∠E=70°3.楼梯的高度3米,水平宽度8米,现要在楼梯的表面铺地毯,地毯每米16元,求购买地毯至少需花多少钱?4.如图,将△ABC沿着从A到D的方向平移后得到△DEF,若AB=4cm,BE=3cm,CE=1cm.(1)指出平移的距离是多少?(2)求线段BF的长.5.平移方格纸中的图形(如图所示),使A点平移到A′点处,画出平移后的图形,并写上一句贴切、诙谐的解说词.
课堂小结:本节课你的收获是什么?
课后作业:1.课本P21习题7.3第1、2、3题.2.(选做题)如图所示,一块蓝色正方形板,边长18cm,上面横竖各两道红条,红条宽都是2cm,问蓝色部分面积是多少?
图形的平移
教学目标:
1.认识平移的概念及平移的不变性,理解平移图形中对应线段平行且相等的性质;2.能按要求作出简单平面图形平移后的图形,能用平移的性质解决实际问题.
教学重点:
理解图形平移的基本性质,并能按要求作出简单平面图形平移后的图形.
教学难点:
能运用平移的性质解决实际问题.
教学过程(教师)
新课引入——情景导入:请你判断
小明跟着妈妈乘观光电梯上楼,一会儿,小明兴奋地大叫起来:“妈妈!妈妈!你看我长高了!我比对面的大楼还要高!”小明说的对吗?为什么??
接触平移现象:教师通过多媒体展示(画面)现实生活中平移的具体实例,你还能举出生活中类似的例子吗?根据上述一些现象,你能说明什么样的图形运动称为平移?
辨一辨、议一议:在以下现象中,属于平移的是
(
)
①
在荡秋千的小朋友;②
打气筒打气时,活塞的运动;③
钟摆的摆动;④
传送带上,瓶装饮料的移动.A.①②
B.①③
C.②③
D.②④
例1
如图,4个小三角形都是等边三角形,边长为1.3cm.你能通过平移△ABC得到其他三角形吗?若能,请画出平移方向,并说出平移的距离.
活动探究:把图中的三角形ABC(可记为△ABC)向右平移6个格子,画出所得的△A′B′C′.度量△ABC与△A′B′C′的边、角的大小,你发现什么了呢?你认为图形平移具有什么特征呢?
例2
将A图案剪成若干小块,再分别平移后能够得到B、C、D中的
(
)
A.0个
B.1个
C.2个
D.3个
做一做:在所示的方格纸上,将线段AB向左平移4格.得到线段A′B′,再将线段A′B′向上平移3格,得到线段A″B″,连接对应点的线段AA′与BB′,A′A″与B′B″,AA″与BB″.在连接对应点的线段AA′与BB′,A′A″与B′B″,AA″与BB″的过程中,你有什么发现?
议一议:(1)下图中的四边形A′B′C′D′是怎样由四边形ABCD平移得到的;(2)线段AA′、BB′、CC′、DD′之间有什么关系?(3)取线段AD的中点M,画出点M平移后对应的点M′,连接MM′.线段MM′与线段AA′有什么关系?你能否用一句话来概括这种关系?
例3 已知△ABC和点D,平移△ABC,使△ABC的顶点A移动到了点D的位置.
课堂反馈:1.在下面的六幅图案中,(2)、(3)、(4)、(5)、(6)中的哪个图案可以通过平移图案(1)得到?2.如图,四边形EFGH是由四边形ABCD平移得到的,已知AD=5,∠B=70°,则?(
)A.FG=5,∠G=70°B.EH=5,∠F=70°C.EF=5,∠F=70°D.EF=5,∠E=70°3.楼梯的高度3米,水平宽度8米,现要在楼梯的表面铺地毯,地毯每米16元,求购买地毯至少需花多少钱?4.如图,将△ABC沿着从A到D的方向平移后得到△DEF,若AB=4cm,BE=3cm,CE=1cm.(1)指出平移的距离是多少?(2)求线段BF的长.5.平移方格纸中的图形(如图所示),使A点平移到A′点处,画出平移后的图形,并写上一句贴切、诙谐的解说词.
课堂小结:本节课你的收获是什么?
课后作业:1.课本P21习题7.3第1、2、3题.2.(选做题)如图所示,一块蓝色正方形板,边长18cm,上面横竖各两道红条,红条宽都是2cm,问蓝色部分面积是多少?
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
