苏科版七下数学:9.3多项式乘多项式 教案
文档属性
| 名称 | 苏科版七下数学:9.3多项式乘多项式 教案 |  | |
| 格式 | zip | ||
| 文件大小 | 38.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-16 17:20:00 | ||
图片预览

文档简介
《多项式乘以多项式》教学设计
教学目标:
知识与技能
1、探索多项式与多项式相乘的乘法法则。
2.
能灵活地进行整式的乘法运算。
过程与方法
1、经历探索多项式与多项式相乘的乘法法则的过程,体会乘法分配律的作用以及“整体”和“转化”的数学思想;
2、通过对乘法法则的探索,归纳与描述,发展有条理思考的能力和语言表达能力;
情感、态度与价值观
体验学习和把握数学问题的方法,树立学好数学的信心,培养学习数学的兴趣。
教学重点:多项式的乘法法则及其应用。
教学难点:探索多项式的乘法法则,灵活地进行整式的乘法运算。
关键:多项式的乘法应先转化为单项式与多项式相乘进行运算,进一步转化为单项式的乘法,紧紧扣住这一线索。
教学方法:小组合作,自主学习
教学过程:
1、
课前练习
师:前面我们学习了整式的乘法,快速做一做,看看你掌握的怎样?
计算:
生:交流答案
师:同学们看这道题怎样做?(多媒体展示)他和我们以前所学的有何不同?
生:现在是多项式乘多项式
师:那多项式乘多项式如何去计算呢?这节课我们一起来探究吧!
2、
学习目标(多媒体)
师:看到这个课题你想学习哪些知识呢?
生:交流
师:(多媒体呈现)
1、探究并了解多项式与多项式相乘的法则
2、熟练的运用法则进行运算
三、探求新知
问题助学一:
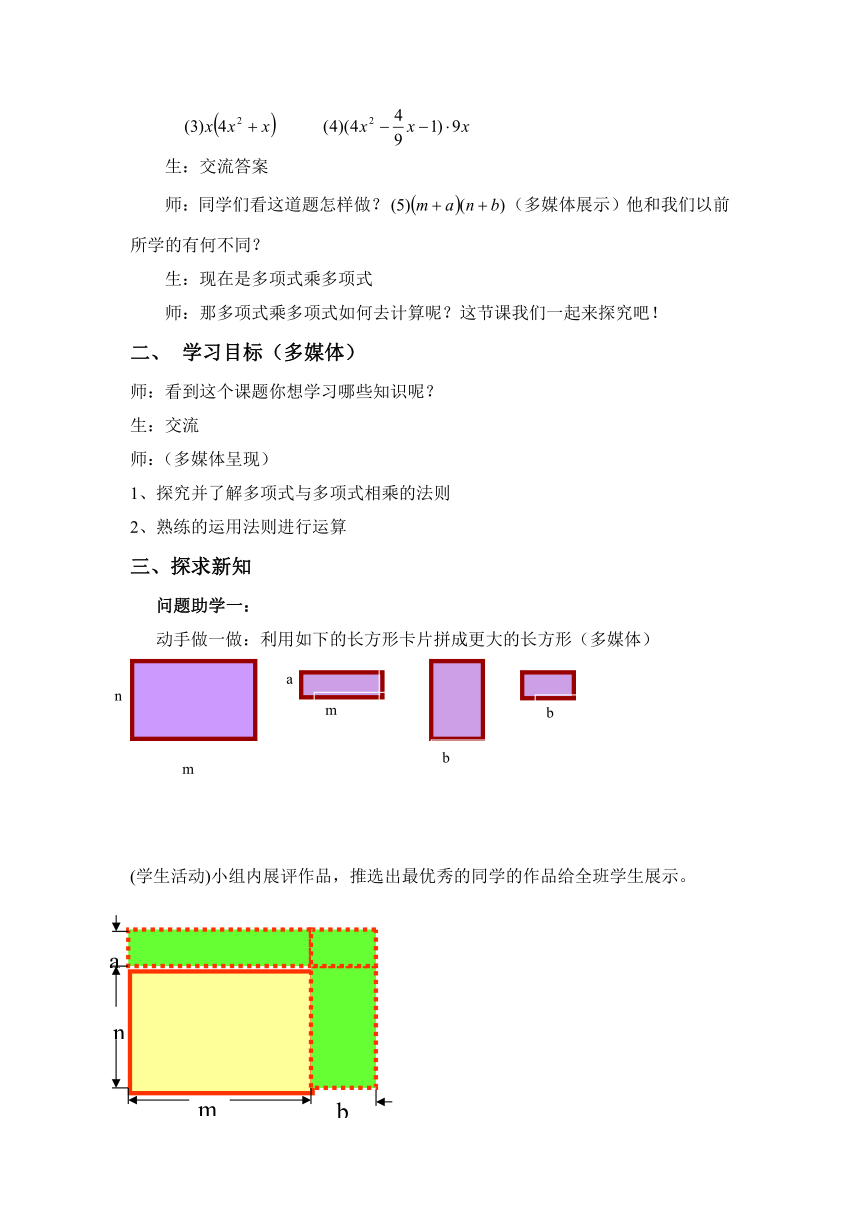
动手做一做:利用如下的长方形卡片拼成更大的长方形(多媒体)
(学生活动)小组内展评作品,推选出最优秀的同学的作品给全班学生展示。
你能用不同的方法表示此长方形的面积吗?
生1:(m+n)(a+b)
生2:ma+mb+na+nb
生3:(m+n)a+(m+n)b
(m+n)(a+b)=(m+n)a+(m+n)b=ma+mb+na+nb
问题助学二:
(多媒体)
1、你能试着说说(m+b)(n+a)=m(n+a)
+
b(n+a)
怎么来的吗?
2、进一步完成m(n+a)
+
b(n+a)
的计算,并说说你的依据
引导学生把其中一个因式看作一个整体,再利用乘法分配律来理解与相乘的结果,从而导出多项式与多项式相乘的法则。
四、诊断指导
归纳、小结多项式乘法法则
(1)文字叙述:多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加
(2)用字母表示
法则的形成是本节课的重点之一。在学生归纳法则的过程中,结合学生讨论的情况,播放法则的形成动画,并在此过程中进行启发讲解,让学生明白两个“每一项”的含义。
五、点拨提升
第一关:(1)(1?x)(0.6?x)
(2)(2x
+
y)(x?y)
设计意图:第一关,目的加强对公式的熟练运用,采用小组合作学习,即先自己动手做一做,再小组讨论兵教兵。最后一起交流小组学习的收获和应该注意的问题。随后在课本随堂练习中做了两道题来检测学生小组学习的情况。
第二关:(1)(a+3)·(b+5);(2)(3x-y)(2x+3y);
设计意图:第二关,题目的设置难度稍微加深,并设置了选做题(多媒体)。
第三关:(1)(3x-2)(2x-3)(x+2);(2)(a-b)(a+b)(a2+b2)
第三关,小组竞赛,题目难度有所提升,目的是检测小组整体合作学习水平,并提高学生小组合作的意识。通过结果评选出优胜小组,奖励相应的分数。
六、课堂小结
1、多项式乘法是用“换元”的方法,将多项式与多项式相乘转化为单项式与多项式相乘。
2、运用法则时,要有序地逐项相乘,做到不重不漏。
3、在含有多项式乘法的混合运算时,要注意运算顺序,计算结果要化简。
七、课堂小测
1、
2、
3、
4、
选作题:
已知的值.
八、板书设计
多项式乘多项式
(m+b)(n+a)
=
mn
+
ma
+
bn
+
ba
n
m
a
m
b
b
n
m
a
b
教学目标:
知识与技能
1、探索多项式与多项式相乘的乘法法则。
2.
能灵活地进行整式的乘法运算。
过程与方法
1、经历探索多项式与多项式相乘的乘法法则的过程,体会乘法分配律的作用以及“整体”和“转化”的数学思想;
2、通过对乘法法则的探索,归纳与描述,发展有条理思考的能力和语言表达能力;
情感、态度与价值观
体验学习和把握数学问题的方法,树立学好数学的信心,培养学习数学的兴趣。
教学重点:多项式的乘法法则及其应用。
教学难点:探索多项式的乘法法则,灵活地进行整式的乘法运算。
关键:多项式的乘法应先转化为单项式与多项式相乘进行运算,进一步转化为单项式的乘法,紧紧扣住这一线索。
教学方法:小组合作,自主学习
教学过程:
1、
课前练习
师:前面我们学习了整式的乘法,快速做一做,看看你掌握的怎样?
计算:
生:交流答案
师:同学们看这道题怎样做?(多媒体展示)他和我们以前所学的有何不同?
生:现在是多项式乘多项式
师:那多项式乘多项式如何去计算呢?这节课我们一起来探究吧!
2、
学习目标(多媒体)
师:看到这个课题你想学习哪些知识呢?
生:交流
师:(多媒体呈现)
1、探究并了解多项式与多项式相乘的法则
2、熟练的运用法则进行运算
三、探求新知
问题助学一:
动手做一做:利用如下的长方形卡片拼成更大的长方形(多媒体)
(学生活动)小组内展评作品,推选出最优秀的同学的作品给全班学生展示。
你能用不同的方法表示此长方形的面积吗?
生1:(m+n)(a+b)
生2:ma+mb+na+nb
生3:(m+n)a+(m+n)b
(m+n)(a+b)=(m+n)a+(m+n)b=ma+mb+na+nb
问题助学二:
(多媒体)
1、你能试着说说(m+b)(n+a)=m(n+a)
+
b(n+a)
怎么来的吗?
2、进一步完成m(n+a)
+
b(n+a)
的计算,并说说你的依据
引导学生把其中一个因式看作一个整体,再利用乘法分配律来理解与相乘的结果,从而导出多项式与多项式相乘的法则。
四、诊断指导
归纳、小结多项式乘法法则
(1)文字叙述:多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加
(2)用字母表示
法则的形成是本节课的重点之一。在学生归纳法则的过程中,结合学生讨论的情况,播放法则的形成动画,并在此过程中进行启发讲解,让学生明白两个“每一项”的含义。
五、点拨提升
第一关:(1)(1?x)(0.6?x)
(2)(2x
+
y)(x?y)
设计意图:第一关,目的加强对公式的熟练运用,采用小组合作学习,即先自己动手做一做,再小组讨论兵教兵。最后一起交流小组学习的收获和应该注意的问题。随后在课本随堂练习中做了两道题来检测学生小组学习的情况。
第二关:(1)(a+3)·(b+5);(2)(3x-y)(2x+3y);
设计意图:第二关,题目的设置难度稍微加深,并设置了选做题(多媒体)。
第三关:(1)(3x-2)(2x-3)(x+2);(2)(a-b)(a+b)(a2+b2)
第三关,小组竞赛,题目难度有所提升,目的是检测小组整体合作学习水平,并提高学生小组合作的意识。通过结果评选出优胜小组,奖励相应的分数。
六、课堂小结
1、多项式乘法是用“换元”的方法,将多项式与多项式相乘转化为单项式与多项式相乘。
2、运用法则时,要有序地逐项相乘,做到不重不漏。
3、在含有多项式乘法的混合运算时,要注意运算顺序,计算结果要化简。
七、课堂小测
1、
2、
3、
4、
选作题:
已知的值.
八、板书设计
多项式乘多项式
(m+b)(n+a)
=
mn
+
ma
+
bn
+
ba
n
m
a
m
b
b
n
m
a
b
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
