函数的奇偶性
图片预览











文档简介
(共65张PPT)
函数的奇偶性
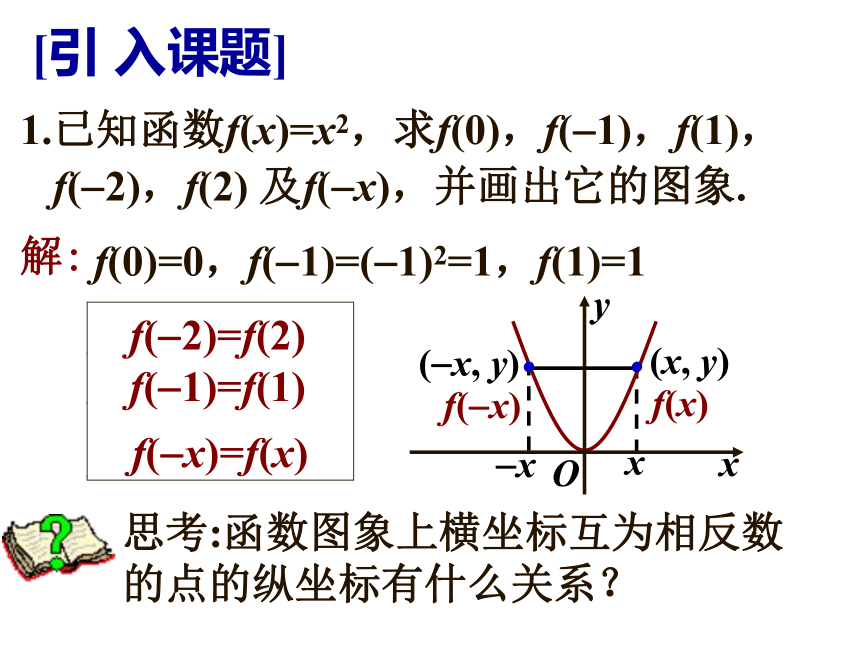
1.已知函数f(x)=x2,求f(0),f( 1),f(1), f( 2),f(2) 及f( x),并画出它的图象.
解:
f( 2)=( 2)2=4 f(2)=4
f(0)=0,f( 1)=( 1)2=1,f(1)=1
f( x)=( x)2=x2
思考:函数图象上横坐标互为相反数的点的纵坐标有什么关系?
f( 2)=f(2) f( 1)=f(1)
f( x)=f(x)
( x, y)
(x, y)
f( x)
f(x)
x
y
O
x
x
[引 入课题]
2.已知f(x)=x3,求f(0),f( 1),f(1),f( 2), f(2)及f( x),并画出它的图象.
2.已知f(x)=x3,求f(0),f( 1),f(1),f( 2), f(2)及f( x),并画出它的图象.
f( 2)=( 2)3= 8 f(2)=8
f(0)=0,f( 1)=( 1)3= 1,f(1)=1
f( x)=( x)3= x3
解:
2.已知f(x)=x3,求f(0),f( 1),f(1),f( 2), f(2)及f( x),并画出它的图象.
f( 2)=( 2)3= 8 f(2)=8
f(0)=0,f( 1)=( 1)3= 1,f(1)=1
f( x)=( x)3= x3
解:
x
y
O
2.已知f(x)=x3,求f(0),f( 1),f(1),f( 2), f(2)及f( x),并画出它的图象.
f( 2)=( 2)3= 8 f(2)=8
f(0)=0,f( 1)=( 1)3= 1,f(1)=1
f( x)=( x)3= x3
解:
思考:函数图象上横坐标互为相反数的点的纵坐标有什么关系?
x
y
O
2.已知f(x)=x3,求f(0),f( 1),f(1),f( 2), f(2)及f( x),并画出它的图象.
f( 2)=( 2)3= 8 f(2)=8
f(0)=0,f( 1)=( 1)3= 1,f(1)=1
f( x)=( x)3= x3
解:
思考:函数图象上横坐标互为相反数的点的纵坐标有什么关系?
f( 2)= f(2) f( 1)= f(1)
x
y
O
2.已知f(x)=x3,求f(0),f( 1),f(1),f( 2), f(2)及f( x),并画出它的图象.
f( 2)=( 2)3= 8 f(2)=8
f(0)=0,f( 1)=( 1)3= 1,f(1)=1
f( x)=( x)3= x3
解:
思考:函数图象上横坐标互为相反数的点的纵坐标有什么关系?
f( 2)= f(2) f( 1)= f(1)
f( x)= f(x)
x
y
O
2.已知f(x)=x3,求f(0),f( 1),f(1),f( 2), f(2)及f( x),并画出它的图象.
f( 2)=( 2)3= 8 f(2)=8
f(0)=0,f( 1)=( 1)3= 1,f(1)=1
f( x)=( x)3= x3
解:
思考:函数图象上横坐标互为相反数的点的纵坐标有什么关系?
f( 2)= f(2) f( 1)= f(1)
f( x)= f(x)
x
y
O
(x, y)
( x, y)
x
x
偶函数定义: 如果对于f(x)定义域内的任意一个x,都有f( x)=f(x),那么函数f(x)就叫偶函数.
[函数奇偶性的概念]
偶函数定义: 如果对于f(x)定义域内的任意一个x,都有f( x)=f(x),那么函数f(x)就叫偶函数.
[函数奇偶性的概念]
奇函数定义: 如果对于f(x)定义域内的任意一个x,都有f( x)= f(x),那么函数f(x)就叫奇函数.
[对奇函数、偶函数定义的说明]
函数具有奇偶性的前提是:定义域关
于原点对称.
[对奇函数、偶函数定义的说明]
函数具有奇偶性的前提是:定义域关
于原点对称.
[对奇函数、偶函数定义的说明]
[a, b]
[-b,-a]
x
O
2. 若f(x)为奇函数,则f( x)= f(x)成立. 若f(x)为偶函数, 则f( x)=f(x)成立.
[对奇函数、偶函数定义的说明]
函数具有奇偶性的前提是:定义域关
于原点对称.
[a, b]
[-b,-a]
x
O
2. 若f(x)为奇函数,则f( x)= f(x)成立. 若f(x)为偶函数, 则f( x)=f(x)成立.
3. 如果一个函数f(x)是奇函数或偶函数,
那么我们就说函数f(x) 具有奇偶性.
[对奇函数、偶函数定义的说明]
函数具有奇偶性的前提是:定义域关
于原点对称.
[a, b]
[-b,-a]
x
O
① f(x)=x4 _______
② f(x)=x ________
③ f(x)=x5 _______
[练习1] 说出下列函数的奇偶性:
⑤ f(x)=x 2 _______
⑥ f(x)=x 3 _______
④ f(x)=x 1_______
① f(x)=x4 _______
② f(x)=x ________
③ f(x)=x5 _______
[练习1] 说出下列函数的奇偶性:
偶函数
⑤ f(x)=x 2 _______
⑥ f(x)=x 3 _______
④ f(x)=x 1_______
① f(x)=x4 _______
② f(x)=x ________
③ f(x)=x5 _______
[练习1] 说出下列函数的奇偶性:
偶函数
奇函数
⑤ f(x)=x 2 _______
⑥ f(x)=x 3 _______
④ f(x)=x 1_______
① f(x)=x4 _______
② f(x)=x ________
③ f(x)=x5 _______
[练习1] 说出下列函数的奇偶性:
偶函数
奇函数
奇函数
⑤ f(x)=x 2 _______
⑥ f(x)=x 3 _______
④ f(x)=x 1_______
① f(x)=x4 _______
② f(x)=x ________
③ f(x)=x5 _______
[练习1] 说出下列函数的奇偶性:
偶函数
奇函数
奇函数
⑤ f(x)=x 2 _______
⑥ f(x)=x 3 _______
④ f(x)=x 1_______
奇函数
① f(x)=x4 _______
② f(x)=x ________
③ f(x)=x5 _______
[练习1] 说出下列函数的奇偶性:
偶函数
奇函数
奇函数
⑤ f(x)=x 2 _______
⑥ f(x)=x 3 _______
④ f(x)=x 1_______
奇函数
偶函数
① f(x)=x4 _______
② f(x)=x ________
③ f(x)=x5 _______
[练习1] 说出下列函数的奇偶性:
偶函数
奇函数
奇函数
⑤ f(x)=x 2 _______
⑥ f(x)=x 3 _______
④ f(x)=x 1_______
奇函数
奇函数
偶函数
① f(x)=x4 _______
② f(x)=x ________
③ f(x)=x5 _______
[练习1] 说出下列函数的奇偶性:
偶函数
奇函数
奇函数
⑤ f(x)=x 2 _______
⑥ f(x)=x 3 _______
[结论] 一般的,对于形如f(x)=xn的函数:
④ f(x)=x 1_______
奇函数
奇函数
偶函数
① f(x)=x4 _______
② f(x)=x ________
③ f(x)=x5 _______
[练习1] 说出下列函数的奇偶性:
偶函数
奇函数
奇函数
⑤ f(x)=x 2 _______
⑥ f(x)=x 3 _______
[结论] 一般的,对于形如f(x)=xn的函数:
若n为偶数,则它为偶函数. 若n为奇数,则它为奇函数.
④ f(x)=x 1_______
奇函数
奇函数
偶函数
(1) f(x)=x3+2x (2) f(x)=2x4+3x2
[例1] 判断下列函数的奇偶性:
= (x3+2x) = f(x)
解:
∵f( x)=( x)3+2( x)
= x3 2x
∴f(x)为奇函数
定义域为R
(1) f(x)=x3+2x (2) f(x)=2x4+3x2
[例1] 判断下列函数的奇偶性:
= (x3+2x) = f(x)
解:
∵f( x)=( x)3+2( x)
= x3 2x
∴f(x)为奇函数
∵f( x)=2( x)4+3( x)2
=2x4+3x2 =f(x)
∴f(x)为偶函数
定义域为R
解:
定义域为R
(1) f(x)=x3+2x (2) f(x)=2x4+3x2
[例1] 判断下列函数的奇偶性:
[小结] 用定义判断函数奇偶性的步骤:
(1) 先求定义域,看是否关于原点对称;
(2) 再判断f( x)= f(x)或f( x)=f(x)是否 恒成立.
[小结] 用定义判断函数奇偶性的步骤:
[练习2] 判断下列函数的奇偶性:
[练习2] 判断下列函数的奇偶性:
∴f(x)为奇函数
定义域为{x|x≠0}
解:
[练习2] 判断下列函数的奇偶性:
∴f(x)为奇函数
∵f( x)= ( x)2+1 = x2+1
∴f(x)为偶函数
定义域为{x|x≠0}
定义域为R
=f(x)
解:
解:
(3) f(x)=5 (4) f(x)=0
(3) f(x)=5 (4) f(x)=0
解:
f(x)的定义域为R ∵f( x)=f(x)=5 ∴f(x)为偶函数
(3) f(x)=5 (4) f(x)=0
解:
f(x)的定义域为R ∵f( x)=f(x)=5 ∴f(x)为偶函数
5
O
x
y
(3) f(x)=5 (4) f(x)=0
定义域为R ∵ f( x)=0=f(x)又 f( x)=0= f(x) ∴f(x)为既奇又偶函数
解:
f(x)的定义域为R ∵f( x)=f(x)=5 ∴f(x)为偶函数
解:
5
O
x
y
(3) f(x)=5 (4) f(x)=0
定义域为R ∵ f( x)=0=f(x)又 f( x)=0= f(x) ∴f(x)为既奇又偶函数
解:
f(x)的定义域为R ∵f( x)=f(x)=5 ∴f(x)为偶函数
解:
5
O
x
y
O
x
y
(3) f(x)=5 (4) f(x)=0
定义域为R ∵ f( x)=0=f(x)又 f( x)=0= f(x) ∴f(x)为既奇又偶函数
[结论] 函数f(x)=0 (定义域关于原点对称)为既奇又偶函数.
解:
f(x)的定义域为R ∵f( x)=f(x)=5 ∴f(x)为偶函数
解:
5
O
x
y
O
x
y
∵f( 1)=0, f(1)=2 ∴f( 1)≠f(1), f( 1)≠ f(1) ∴f(x)为非奇非 偶函数
解:
∵f( 1)=0, f(1)=2 ∴f( 1)≠f(1), f( 1)≠ f(1) ∴f(x)为非奇非 偶函数
定义域为[0, +∞) ∵定义域不关于 原点对称 ∴f(x)为非奇非 偶函数
解:
解:
解:
定义域为R
解:
定义域为R
[小结] 根据奇偶性,函数可划分为四类:
解:
定义域为R
[小结] 根据奇偶性,函数可划分为四类:
(1) 奇函数 (2) 偶函数 (3) 既奇又偶函数 (4) 非奇非偶函数
[例2]
(1) 求函数的定义域; (2) 化简函数表达式; (3) 判断函数的奇偶性.
[例2]
(1) 求函数的定义域; (2) 化简函数表达式; (3) 判断函数的奇偶性.
解:
[奇偶函数图象的性质]
奇函数的图象(如y=x3 )
[奇偶函数图象的性质]
y
x
O
a
P'( a, f( a))
P(a, f(a))
a
奇函数的图象(如y=x3 )
[奇偶函数图象的性质]
y
x
O
a
P'( a, f( a))
P(a, f(a))
a
( a, f(a))
奇函数的图象(如y=x3 )
[奇偶函数图象的性质]
偶函数的图象(如y=x2)
y
x
O
a
P'( a, f( a))
P(a, f(a))
a
( a, f(a))
奇函数的图象(如y=x3 )
[奇偶函数图象的性质]
偶函数的图象(如y=x2)
y
x
O
a
P'( a, f( a))
P(a, f(a))
a
( a, f(a))
y
x
O
a
a
P'( a, f( a))
P(a, f(a))
奇函数的图象(如y=x3 )
[奇偶函数图象的性质]
偶函数的图象(如y=x2)
y
x
O
a
P'( a, f( a))
P(a, f(a))
a
( a, f(a))
y
x
O
a
a
P'( a, f( a))
P(a, f(a))
( a, f(a))
奇函数的图象(如y=x3 )
[奇偶函数图象的性质]
[奇偶函数图象的性质]
1.奇函数的图象关于原点对称. 反过来,如果一个函数的图象关于 原点对称,那么这个函数为奇函数.
2. 偶函数的图象关于y轴对称.
反过来,如果一个函数的图象关于y轴对称,那么这个函数为偶函数.
[奇偶函数图象的性质]
1.奇函数的图象关于原点对称. 反过来,如果一个函数的图象关于 原点对称,那么这个函数为奇函数.
[注] 奇偶函数图象的性质可用于:
① 判断函数的奇偶性;
② 简化函数图象的画法.
[例3] 已知函数y=f(x)是偶函数,它在y轴右边的图象如图,画出y=f(x)在 y轴左边的图象.
O
y
x
O
y
x
解:
[例3] 已知函数y=f(x)是偶函数,它在y轴右边的图象如图,画出y=f(x)在 y轴左边的图象.
O
y
x
解:
[例3] 已知函数y=f(x)是偶函数,它在y轴右边的图象如图,画出y=f(x)在 y轴左边的图象.
O
y
x
解:
[例3] 已知函数y=f(x)是偶函数,它在y轴右边的图象如图,画出y=f(x)在 y轴左边的图象.
[本课小结]
1.两个定义: 对于f(x)定义域内的任意一个x,
2.两个性质:
函数的奇偶性
1.已知函数f(x)=x2,求f(0),f( 1),f(1), f( 2),f(2) 及f( x),并画出它的图象.
解:
f( 2)=( 2)2=4 f(2)=4
f(0)=0,f( 1)=( 1)2=1,f(1)=1
f( x)=( x)2=x2
思考:函数图象上横坐标互为相反数的点的纵坐标有什么关系?
f( 2)=f(2) f( 1)=f(1)
f( x)=f(x)
( x, y)
(x, y)
f( x)
f(x)
x
y
O
x
x
[引 入课题]
2.已知f(x)=x3,求f(0),f( 1),f(1),f( 2), f(2)及f( x),并画出它的图象.
2.已知f(x)=x3,求f(0),f( 1),f(1),f( 2), f(2)及f( x),并画出它的图象.
f( 2)=( 2)3= 8 f(2)=8
f(0)=0,f( 1)=( 1)3= 1,f(1)=1
f( x)=( x)3= x3
解:
2.已知f(x)=x3,求f(0),f( 1),f(1),f( 2), f(2)及f( x),并画出它的图象.
f( 2)=( 2)3= 8 f(2)=8
f(0)=0,f( 1)=( 1)3= 1,f(1)=1
f( x)=( x)3= x3
解:
x
y
O
2.已知f(x)=x3,求f(0),f( 1),f(1),f( 2), f(2)及f( x),并画出它的图象.
f( 2)=( 2)3= 8 f(2)=8
f(0)=0,f( 1)=( 1)3= 1,f(1)=1
f( x)=( x)3= x3
解:
思考:函数图象上横坐标互为相反数的点的纵坐标有什么关系?
x
y
O
2.已知f(x)=x3,求f(0),f( 1),f(1),f( 2), f(2)及f( x),并画出它的图象.
f( 2)=( 2)3= 8 f(2)=8
f(0)=0,f( 1)=( 1)3= 1,f(1)=1
f( x)=( x)3= x3
解:
思考:函数图象上横坐标互为相反数的点的纵坐标有什么关系?
f( 2)= f(2) f( 1)= f(1)
x
y
O
2.已知f(x)=x3,求f(0),f( 1),f(1),f( 2), f(2)及f( x),并画出它的图象.
f( 2)=( 2)3= 8 f(2)=8
f(0)=0,f( 1)=( 1)3= 1,f(1)=1
f( x)=( x)3= x3
解:
思考:函数图象上横坐标互为相反数的点的纵坐标有什么关系?
f( 2)= f(2) f( 1)= f(1)
f( x)= f(x)
x
y
O
2.已知f(x)=x3,求f(0),f( 1),f(1),f( 2), f(2)及f( x),并画出它的图象.
f( 2)=( 2)3= 8 f(2)=8
f(0)=0,f( 1)=( 1)3= 1,f(1)=1
f( x)=( x)3= x3
解:
思考:函数图象上横坐标互为相反数的点的纵坐标有什么关系?
f( 2)= f(2) f( 1)= f(1)
f( x)= f(x)
x
y
O
(x, y)
( x, y)
x
x
偶函数定义: 如果对于f(x)定义域内的任意一个x,都有f( x)=f(x),那么函数f(x)就叫偶函数.
[函数奇偶性的概念]
偶函数定义: 如果对于f(x)定义域内的任意一个x,都有f( x)=f(x),那么函数f(x)就叫偶函数.
[函数奇偶性的概念]
奇函数定义: 如果对于f(x)定义域内的任意一个x,都有f( x)= f(x),那么函数f(x)就叫奇函数.
[对奇函数、偶函数定义的说明]
函数具有奇偶性的前提是:定义域关
于原点对称.
[对奇函数、偶函数定义的说明]
函数具有奇偶性的前提是:定义域关
于原点对称.
[对奇函数、偶函数定义的说明]
[a, b]
[-b,-a]
x
O
2. 若f(x)为奇函数,则f( x)= f(x)成立. 若f(x)为偶函数, 则f( x)=f(x)成立.
[对奇函数、偶函数定义的说明]
函数具有奇偶性的前提是:定义域关
于原点对称.
[a, b]
[-b,-a]
x
O
2. 若f(x)为奇函数,则f( x)= f(x)成立. 若f(x)为偶函数, 则f( x)=f(x)成立.
3. 如果一个函数f(x)是奇函数或偶函数,
那么我们就说函数f(x) 具有奇偶性.
[对奇函数、偶函数定义的说明]
函数具有奇偶性的前提是:定义域关
于原点对称.
[a, b]
[-b,-a]
x
O
① f(x)=x4 _______
② f(x)=x ________
③ f(x)=x5 _______
[练习1] 说出下列函数的奇偶性:
⑤ f(x)=x 2 _______
⑥ f(x)=x 3 _______
④ f(x)=x 1_______
① f(x)=x4 _______
② f(x)=x ________
③ f(x)=x5 _______
[练习1] 说出下列函数的奇偶性:
偶函数
⑤ f(x)=x 2 _______
⑥ f(x)=x 3 _______
④ f(x)=x 1_______
① f(x)=x4 _______
② f(x)=x ________
③ f(x)=x5 _______
[练习1] 说出下列函数的奇偶性:
偶函数
奇函数
⑤ f(x)=x 2 _______
⑥ f(x)=x 3 _______
④ f(x)=x 1_______
① f(x)=x4 _______
② f(x)=x ________
③ f(x)=x5 _______
[练习1] 说出下列函数的奇偶性:
偶函数
奇函数
奇函数
⑤ f(x)=x 2 _______
⑥ f(x)=x 3 _______
④ f(x)=x 1_______
① f(x)=x4 _______
② f(x)=x ________
③ f(x)=x5 _______
[练习1] 说出下列函数的奇偶性:
偶函数
奇函数
奇函数
⑤ f(x)=x 2 _______
⑥ f(x)=x 3 _______
④ f(x)=x 1_______
奇函数
① f(x)=x4 _______
② f(x)=x ________
③ f(x)=x5 _______
[练习1] 说出下列函数的奇偶性:
偶函数
奇函数
奇函数
⑤ f(x)=x 2 _______
⑥ f(x)=x 3 _______
④ f(x)=x 1_______
奇函数
偶函数
① f(x)=x4 _______
② f(x)=x ________
③ f(x)=x5 _______
[练习1] 说出下列函数的奇偶性:
偶函数
奇函数
奇函数
⑤ f(x)=x 2 _______
⑥ f(x)=x 3 _______
④ f(x)=x 1_______
奇函数
奇函数
偶函数
① f(x)=x4 _______
② f(x)=x ________
③ f(x)=x5 _______
[练习1] 说出下列函数的奇偶性:
偶函数
奇函数
奇函数
⑤ f(x)=x 2 _______
⑥ f(x)=x 3 _______
[结论] 一般的,对于形如f(x)=xn的函数:
④ f(x)=x 1_______
奇函数
奇函数
偶函数
① f(x)=x4 _______
② f(x)=x ________
③ f(x)=x5 _______
[练习1] 说出下列函数的奇偶性:
偶函数
奇函数
奇函数
⑤ f(x)=x 2 _______
⑥ f(x)=x 3 _______
[结论] 一般的,对于形如f(x)=xn的函数:
若n为偶数,则它为偶函数. 若n为奇数,则它为奇函数.
④ f(x)=x 1_______
奇函数
奇函数
偶函数
(1) f(x)=x3+2x (2) f(x)=2x4+3x2
[例1] 判断下列函数的奇偶性:
= (x3+2x) = f(x)
解:
∵f( x)=( x)3+2( x)
= x3 2x
∴f(x)为奇函数
定义域为R
(1) f(x)=x3+2x (2) f(x)=2x4+3x2
[例1] 判断下列函数的奇偶性:
= (x3+2x) = f(x)
解:
∵f( x)=( x)3+2( x)
= x3 2x
∴f(x)为奇函数
∵f( x)=2( x)4+3( x)2
=2x4+3x2 =f(x)
∴f(x)为偶函数
定义域为R
解:
定义域为R
(1) f(x)=x3+2x (2) f(x)=2x4+3x2
[例1] 判断下列函数的奇偶性:
[小结] 用定义判断函数奇偶性的步骤:
(1) 先求定义域,看是否关于原点对称;
(2) 再判断f( x)= f(x)或f( x)=f(x)是否 恒成立.
[小结] 用定义判断函数奇偶性的步骤:
[练习2] 判断下列函数的奇偶性:
[练习2] 判断下列函数的奇偶性:
∴f(x)为奇函数
定义域为{x|x≠0}
解:
[练习2] 判断下列函数的奇偶性:
∴f(x)为奇函数
∵f( x)= ( x)2+1 = x2+1
∴f(x)为偶函数
定义域为{x|x≠0}
定义域为R
=f(x)
解:
解:
(3) f(x)=5 (4) f(x)=0
(3) f(x)=5 (4) f(x)=0
解:
f(x)的定义域为R ∵f( x)=f(x)=5 ∴f(x)为偶函数
(3) f(x)=5 (4) f(x)=0
解:
f(x)的定义域为R ∵f( x)=f(x)=5 ∴f(x)为偶函数
5
O
x
y
(3) f(x)=5 (4) f(x)=0
定义域为R ∵ f( x)=0=f(x)又 f( x)=0= f(x) ∴f(x)为既奇又偶函数
解:
f(x)的定义域为R ∵f( x)=f(x)=5 ∴f(x)为偶函数
解:
5
O
x
y
(3) f(x)=5 (4) f(x)=0
定义域为R ∵ f( x)=0=f(x)又 f( x)=0= f(x) ∴f(x)为既奇又偶函数
解:
f(x)的定义域为R ∵f( x)=f(x)=5 ∴f(x)为偶函数
解:
5
O
x
y
O
x
y
(3) f(x)=5 (4) f(x)=0
定义域为R ∵ f( x)=0=f(x)又 f( x)=0= f(x) ∴f(x)为既奇又偶函数
[结论] 函数f(x)=0 (定义域关于原点对称)为既奇又偶函数.
解:
f(x)的定义域为R ∵f( x)=f(x)=5 ∴f(x)为偶函数
解:
5
O
x
y
O
x
y
∵f( 1)=0, f(1)=2 ∴f( 1)≠f(1), f( 1)≠ f(1) ∴f(x)为非奇非 偶函数
解:
∵f( 1)=0, f(1)=2 ∴f( 1)≠f(1), f( 1)≠ f(1) ∴f(x)为非奇非 偶函数
定义域为[0, +∞) ∵定义域不关于 原点对称 ∴f(x)为非奇非 偶函数
解:
解:
解:
定义域为R
解:
定义域为R
[小结] 根据奇偶性,函数可划分为四类:
解:
定义域为R
[小结] 根据奇偶性,函数可划分为四类:
(1) 奇函数 (2) 偶函数 (3) 既奇又偶函数 (4) 非奇非偶函数
[例2]
(1) 求函数的定义域; (2) 化简函数表达式; (3) 判断函数的奇偶性.
[例2]
(1) 求函数的定义域; (2) 化简函数表达式; (3) 判断函数的奇偶性.
解:
[奇偶函数图象的性质]
奇函数的图象(如y=x3 )
[奇偶函数图象的性质]
y
x
O
a
P'( a, f( a))
P(a, f(a))
a
奇函数的图象(如y=x3 )
[奇偶函数图象的性质]
y
x
O
a
P'( a, f( a))
P(a, f(a))
a
( a, f(a))
奇函数的图象(如y=x3 )
[奇偶函数图象的性质]
偶函数的图象(如y=x2)
y
x
O
a
P'( a, f( a))
P(a, f(a))
a
( a, f(a))
奇函数的图象(如y=x3 )
[奇偶函数图象的性质]
偶函数的图象(如y=x2)
y
x
O
a
P'( a, f( a))
P(a, f(a))
a
( a, f(a))
y
x
O
a
a
P'( a, f( a))
P(a, f(a))
奇函数的图象(如y=x3 )
[奇偶函数图象的性质]
偶函数的图象(如y=x2)
y
x
O
a
P'( a, f( a))
P(a, f(a))
a
( a, f(a))
y
x
O
a
a
P'( a, f( a))
P(a, f(a))
( a, f(a))
奇函数的图象(如y=x3 )
[奇偶函数图象的性质]
[奇偶函数图象的性质]
1.奇函数的图象关于原点对称. 反过来,如果一个函数的图象关于 原点对称,那么这个函数为奇函数.
2. 偶函数的图象关于y轴对称.
反过来,如果一个函数的图象关于y轴对称,那么这个函数为偶函数.
[奇偶函数图象的性质]
1.奇函数的图象关于原点对称. 反过来,如果一个函数的图象关于 原点对称,那么这个函数为奇函数.
[注] 奇偶函数图象的性质可用于:
① 判断函数的奇偶性;
② 简化函数图象的画法.
[例3] 已知函数y=f(x)是偶函数,它在y轴右边的图象如图,画出y=f(x)在 y轴左边的图象.
O
y
x
O
y
x
解:
[例3] 已知函数y=f(x)是偶函数,它在y轴右边的图象如图,画出y=f(x)在 y轴左边的图象.
O
y
x
解:
[例3] 已知函数y=f(x)是偶函数,它在y轴右边的图象如图,画出y=f(x)在 y轴左边的图象.
O
y
x
解:
[例3] 已知函数y=f(x)是偶函数,它在y轴右边的图象如图,画出y=f(x)在 y轴左边的图象.
[本课小结]
1.两个定义: 对于f(x)定义域内的任意一个x,
2.两个性质:
