02河北省普通高中学业水平考试模拟试卷02
文档属性
| 名称 | 02河北省普通高中学业水平考试模拟试卷02 |  | |
| 格式 | zip | ||
| 文件大小 | 142.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-05-13 17:01:24 | ||
图片预览


文档简介
河北省普通高中学业水平考试模拟试卷02
一、选择题:(本题共25小题,1—15小题每小题2分,16—25小题每小题3共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知全集U=R,集合A={x|x2-x=0},B={x|-1A.{0} B. {1} C.{0,1} D.
2.角终边过点,则=
A. B. C. D.
3.某单位有职工750人,其中青年职工350人,中年职工250人,老年职工150人,为了了解该单位职工的健康情况,用分层抽样的方法从中抽取样本 . 若样本中的青年职工为7人,则样本容量为
A.7 B.15 C.25 D.35
4.的值为
A.-4 B.4 C.2 D.-2
5.m, n, l是三条不同的直线,是三个不同的平面,下列命题中的真命题是
A.若m, n与l都垂直,则m∥n B.若m∥,m∥n,则n∥
C.若m, n∥且∥,则mn D.若,,则∥
6.以点(2,-1)为圆心且与直线相切的圆的方程为
A. B.
C. D.
7.等差数列中,,,则的值为
A.15 B.23 C.25 D.37
8.若,,则等于
A. B. C. D.
9.设函数则的值为
A. B. C. D.
10.已知向量,且∥,则x =
A.9 B.6 C.5 D.1
11.如图是一个几何体的三视图,则这个几何体的体积是
A.27 B.30 C.33 D.36
12.若,则下列结论正确的是
A. B. C. D.
13.下列函数中,最小正周期为,且图象关于直线对称的是
A. B.
C. D.
14.设等比数列{an}的前n项和为Sn,若S10:S5=1:2,则S15:S5=
A.3:4 B.2:3 C.1:2 D.1:3
15.已知是所在平面内一点,为边中点,且,那么
A. B. C. D.
16.实数的最大值为
A.—1 B.0 C.2 D.4
17.为了得到函数的图像,只需把函数的图像
A.向左平移个长度单位 B.向右平移个长度单位
C.向左平移个长度单位 D.向右平移个长度单位
18.若,则
A. B. C. D.
19.正方体-中,与平面所成角的余弦值为
A. B. C. D.
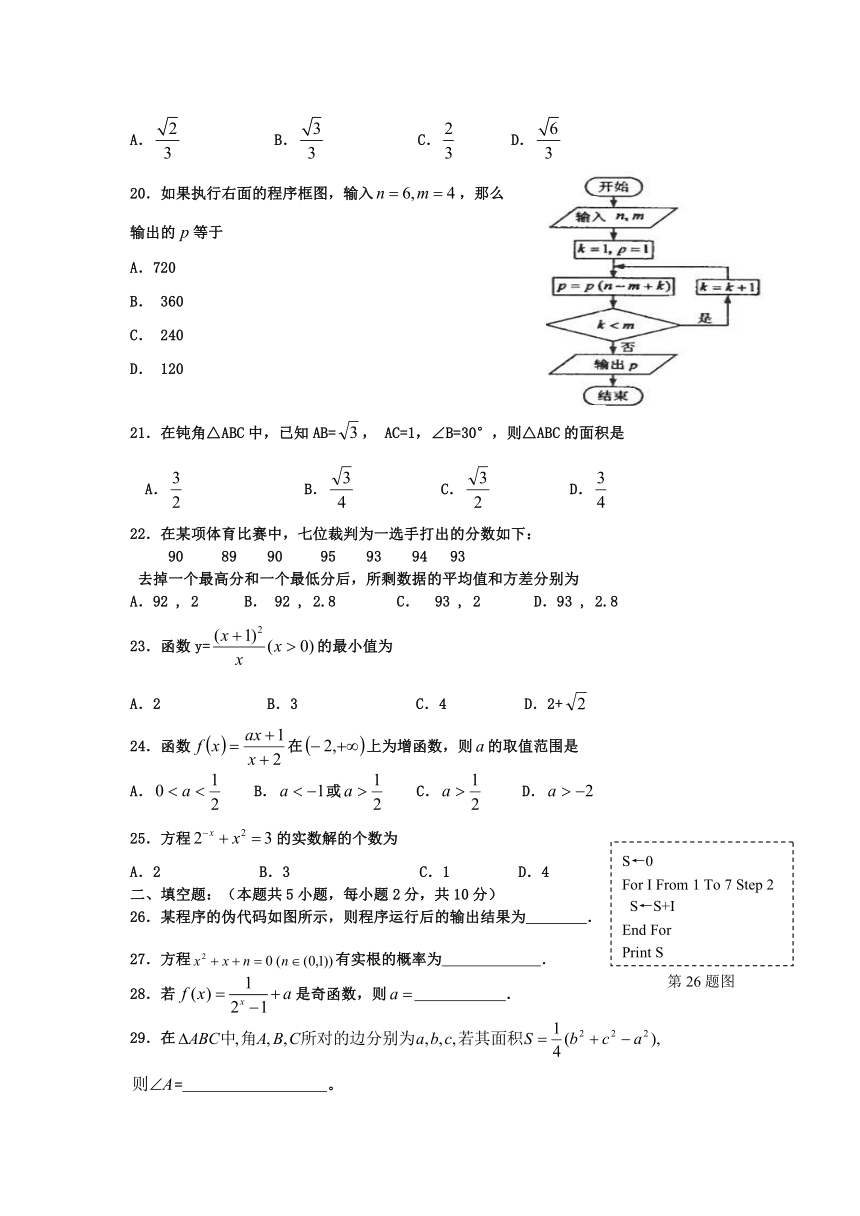
20.如果执行右面的程序框图,输入,那么
输出的等于
A.720
B. 360
C. 240
D. 120
21.在钝角△ABC中,已知AB=, AC=1,∠B=30°,则△ABC的面积是
A. B. C. D.
22.在某项体育比赛中,七位裁判为一选手打出的分数如下:
90 89 90 95 93 94 93
去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为
A.92 , 2 B. 92 , 2.8 C. 93 , 2 D.93 , 2.8
23.函数y=的最小值为
A.2 B.3 C.4 D.2+
24.函数在上为增函数,则的取值范围是
A. B.或 C. D.
25.方程的实数解的个数为
A.2 B.3 C.1 D.4
二、填空题:(本题共5小题,每小题2分,共10分)
26.某程序的伪代码如图所示,则程序运行后的输出结果为 .
27.方程有实根的概率为 .
28.若是奇函数,则 .
29.在
= 。
30.圆关于直线对称,则ab的取值范围是
三、解答题:(本大题共3小题,30分.解答应写出文字说明,证明过程或演算步骤.)
31.(本小题满分8分)已知函数.(Ⅰ)求的最小正周期; (Ⅱ)设,求的值域和单调递增区间.
32.(本小题满分10分)设等比数列的公比为, 前项和为, 若成等差数列, 求的值.
33.(本小题满分12分)如图,在四棱锥中,底面是边长为的正方形,侧面底面,且,若、分别为线段、的中点.
(1) 求证:直线// 平面;
(2) 求证:平面平面;
(3) 求二面角的正切值.
河北省普通高中学业水平考试模拟试卷02--答案
一.选择题
1 2 3 4 5 6 7 8 9 10 11 12 13
A C B D C C B D A B B D B
14 15 16 17 18 19 20 21 22 23 24 25
A A D B D D B B B C C A
二.填空题
26.答案 16
27.答案
28.答案
29.答案
30.答案
二.解答题
31.解(Ⅰ)∵……………… 2分 的最小正周期为. ………………… 4分
(Ⅱ)∵, , .
的值域为. ……………… 6分
当递减时,递增.
,即.
故的递增区间为. ……………………8分
32.解: 若, 则,
, 不合要求; ………3分
若, 则, …………………6分
, ………………………………………9分
综上, .…………10分
33..(1)证明:连结,在中// ……1分
且平面,平面
………………………………………………………………………3分
(2)证明:因为面面 平面面
所以,平面 ……………………………………………5分
又,所以是等腰直角三角形,且
即…………………………………………………………………7分
,且、面
面
又面 面面…………9分
(3)解:设的中点为,连结,,则
由(Ⅱ)知面,
面
是二面角的平面角……….10分
中,
故所求二面角的正切为 ……12分
3
3
1
正视图
侧视图
俯视图
S←0
For I From 1 To 7 Step 2
S←S+I
End For
Print S
第26题图
一、选择题:(本题共25小题,1—15小题每小题2分,16—25小题每小题3共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知全集U=R,集合A={x|x2-x=0},B={x|-1
2.角终边过点,则=
A. B. C. D.
3.某单位有职工750人,其中青年职工350人,中年职工250人,老年职工150人,为了了解该单位职工的健康情况,用分层抽样的方法从中抽取样本 . 若样本中的青年职工为7人,则样本容量为
A.7 B.15 C.25 D.35
4.的值为
A.-4 B.4 C.2 D.-2
5.m, n, l是三条不同的直线,是三个不同的平面,下列命题中的真命题是
A.若m, n与l都垂直,则m∥n B.若m∥,m∥n,则n∥
C.若m, n∥且∥,则mn D.若,,则∥
6.以点(2,-1)为圆心且与直线相切的圆的方程为
A. B.
C. D.
7.等差数列中,,,则的值为
A.15 B.23 C.25 D.37
8.若,,则等于
A. B. C. D.
9.设函数则的值为
A. B. C. D.
10.已知向量,且∥,则x =
A.9 B.6 C.5 D.1
11.如图是一个几何体的三视图,则这个几何体的体积是
A.27 B.30 C.33 D.36
12.若,则下列结论正确的是
A. B. C. D.
13.下列函数中,最小正周期为,且图象关于直线对称的是
A. B.
C. D.
14.设等比数列{an}的前n项和为Sn,若S10:S5=1:2,则S15:S5=
A.3:4 B.2:3 C.1:2 D.1:3
15.已知是所在平面内一点,为边中点,且,那么
A. B. C. D.
16.实数的最大值为
A.—1 B.0 C.2 D.4
17.为了得到函数的图像,只需把函数的图像
A.向左平移个长度单位 B.向右平移个长度单位
C.向左平移个长度单位 D.向右平移个长度单位
18.若,则
A. B. C. D.
19.正方体-中,与平面所成角的余弦值为
A. B. C. D.
20.如果执行右面的程序框图,输入,那么
输出的等于
A.720
B. 360
C. 240
D. 120
21.在钝角△ABC中,已知AB=, AC=1,∠B=30°,则△ABC的面积是
A. B. C. D.
22.在某项体育比赛中,七位裁判为一选手打出的分数如下:
90 89 90 95 93 94 93
去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为
A.92 , 2 B. 92 , 2.8 C. 93 , 2 D.93 , 2.8
23.函数y=的最小值为
A.2 B.3 C.4 D.2+
24.函数在上为增函数,则的取值范围是
A. B.或 C. D.
25.方程的实数解的个数为
A.2 B.3 C.1 D.4
二、填空题:(本题共5小题,每小题2分,共10分)
26.某程序的伪代码如图所示,则程序运行后的输出结果为 .
27.方程有实根的概率为 .
28.若是奇函数,则 .
29.在
= 。
30.圆关于直线对称,则ab的取值范围是
三、解答题:(本大题共3小题,30分.解答应写出文字说明,证明过程或演算步骤.)
31.(本小题满分8分)已知函数.(Ⅰ)求的最小正周期; (Ⅱ)设,求的值域和单调递增区间.
32.(本小题满分10分)设等比数列的公比为, 前项和为, 若成等差数列, 求的值.
33.(本小题满分12分)如图,在四棱锥中,底面是边长为的正方形,侧面底面,且,若、分别为线段、的中点.
(1) 求证:直线// 平面;
(2) 求证:平面平面;
(3) 求二面角的正切值.
河北省普通高中学业水平考试模拟试卷02--答案
一.选择题
1 2 3 4 5 6 7 8 9 10 11 12 13
A C B D C C B D A B B D B
14 15 16 17 18 19 20 21 22 23 24 25
A A D B D D B B B C C A
二.填空题
26.答案 16
27.答案
28.答案
29.答案
30.答案
二.解答题
31.解(Ⅰ)∵……………… 2分 的最小正周期为. ………………… 4分
(Ⅱ)∵, , .
的值域为. ……………… 6分
当递减时,递增.
,即.
故的递增区间为. ……………………8分
32.解: 若, 则,
, 不合要求; ………3分
若, 则, …………………6分
, ………………………………………9分
综上, .…………10分
33..(1)证明:连结,在中// ……1分
且平面,平面
………………………………………………………………………3分
(2)证明:因为面面 平面面
所以,平面 ……………………………………………5分
又,所以是等腰直角三角形,且
即…………………………………………………………………7分
,且、面
面
又面 面面…………9分
(3)解:设的中点为,连结,,则
由(Ⅱ)知面,
面
是二面角的平面角……….10分
中,
故所求二面角的正切为 ……12分
3
3
1
正视图
侧视图
俯视图
S←0
For I From 1 To 7 Step 2
S←S+I
End For
Print S
第26题图
同课章节目录
