05河北省普通高中学业水平考试模拟试卷05
文档属性
| 名称 | 05河北省普通高中学业水平考试模拟试卷05 | 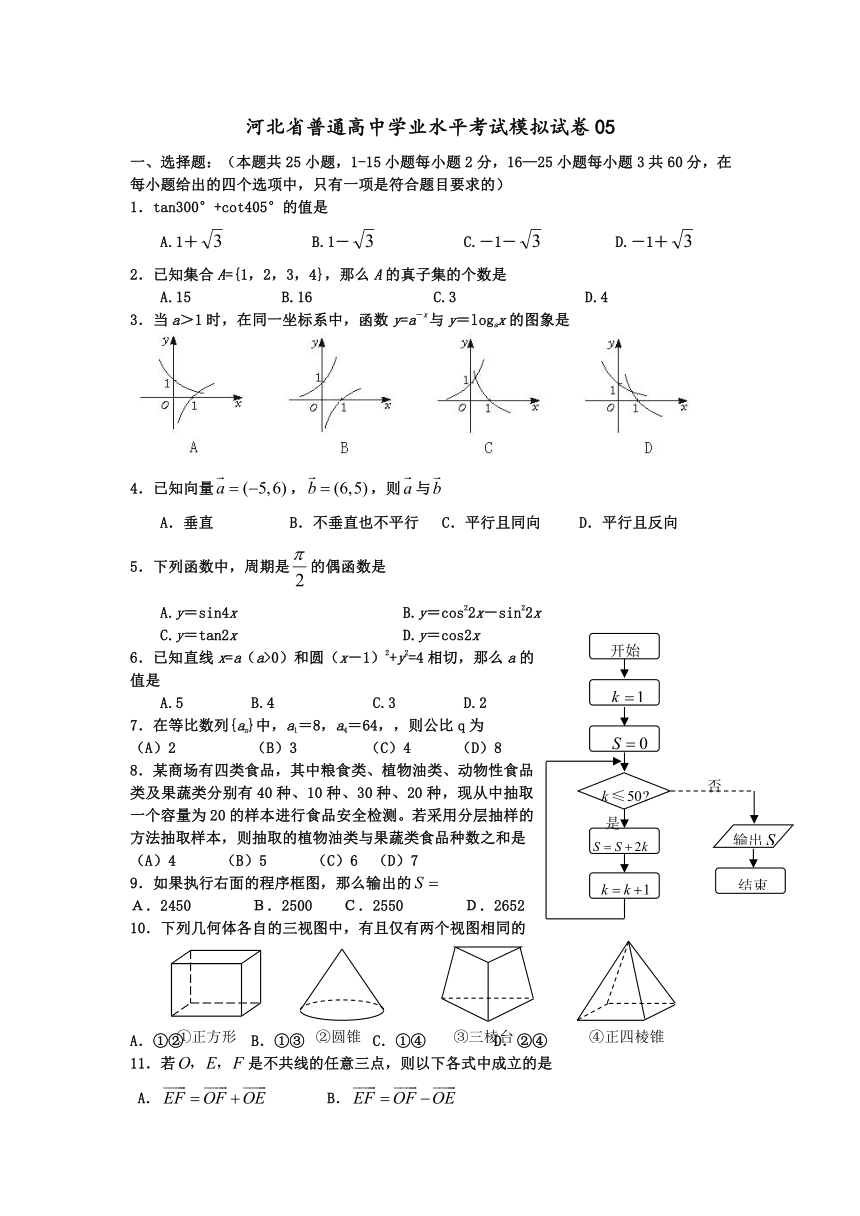 | |
| 格式 | zip | ||
| 文件大小 | 119.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-05-13 17:09:04 | ||
图片预览




文档简介
河北省普通高中学业水平考试模拟试卷05
一、选择题:(本题共25小题,1-15小题每小题2分,16—25小题每小题3共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.tan300°+cot405°的值是
A.1+ B.1- C.-1- D.-1+
2.已知集合A={1,2,3,4},那么A的真子集的个数是
A.15 B.16 C.3 D.4
3.当a>1时,在同一坐标系中,函数y=a-x与y=logax的图象是
4.已知向量,,则与
A.垂直 B.不垂直也不平行 C.平行且同向 D.平行且反向
5.下列函数中,周期是的偶函数是
A.y=sin4x B.y=cos22x-sin22x
C.y=tan2x D.y=cos2x
6.已知直线x=a(a>0)和圆(x-1)2+y2=4相切,那么a的值是
A.5 B.4 C.3 D.2
7.在等比数列{an}中,a1=8,a4=64,,则公比q为
(A)2 (B)3 (C)4 (D)8
8.某商场有四类食品,其中粮食类、植物油类、动物性食品类及果蔬类分别有40种、10种、30种、20种,现从中抽取一个容量为20的样本进行食品安全检测。若采用分层抽样的方法抽取样本,则抽取的植物油类与果蔬类食品种数之和是
(A)4 (B)5 (C)6 (D)7
9.如果执行右面的程序框图,那么输出的
A.2450 B.2500 C.2550 D.2652
10.下列几何体各自的三视图中,有且仅有两个视图相同的
A.①② B.①③ C.①④ D.②④
11.若是不共线的任意三点,则以下各式中成立的是
A. B.
C. D.
12.使sinx≤cosx成立的x的一个变化区间是
A.[-,] B.[-,] C.[-,] D.[0,π]
13.在等比数列()中,若,,则该数列的前10项和为
A. B. C. D.
14.若非零向量、满足|一|=||,则
(A) |2|>|一2| (B) |2|<|一2|
(C) |2|>|2一| (D) |2|<|2一|
15.若A、B、C是△ABC的三个内角,且AA.sinA16.函数的反函数的定义域为
A. B. C. D.
17.图中的图象所表示的函数的解析式为
(A) (0≤x≤2)
(B) (0≤x≤2)
(C) (0≤x≤2)
(D) (0≤x≤2)
18.等差数列{an}的前m项和为30,前2m项和为100,则它的前3m项和为
A.130 B.170 C.210 D.260
19.下列多组点中,三点共线的是
A.(1,4),(-1,2),(3,5) B.(-2,-5),(7,6),(-5,3)
C.(1,0),(0,-),(7,2) D.(0,0),(2,4),(-1,3)
20.已知四个条件,①b>0>a ②0>a>b ③a>0>b ④a>b>0能推出成立的有
A.1个 B.2个 C.3个 D.4个
21.已知,则
A、2 B、-2 C、0 D、
22.在中,,且最大边长和最小边长是方程的两个根,则第三边的长为
A.2 B.3 C.4 D.5
23.连续掷两次骰子分别得到的点数为m、n,则点P(m,n)在直线x+y=5左下方的概率为
A. B. C. D.
24.已知满足约束条件,则的最小值是
A. B. C. D.
25.利用计算器,列出自变量和函数值的对应值如下表:
0.2 0.6 1.0 1.4 1.8 2.2 2.6 3.0 3.4 …
1.149 1.516 2.0 2.639 3.482 4.595 6.063 8.0 10.556 …
0.04 0.36 1.0 1.96 3.24 4.84 6.76 9.0 11.56 …
那么方程的一个根位于下列区间的
A.(0.6,1.0);B.(1.4,1.8);C.(1.8,2.2);D. (2.6,3.0)
二、填空题:(本题共5小题,每小题2分,共10分)
26.不等式的解集是___________
27.已知,则= .
28.等差数列{an}中,a1=2,公差不为零,且a1,a3,a11恰好是某等比数列的前三项,那么该等比数列公比的值等于 .
29.圆x2+y2-2x-2y+1=0上的动点Q到直线3x+4y+8=0距离的最小值为 .
30.函数f(x)=3sinxcosx-4cos2x的最大值是_____.
三、解答题:(本大题共3小题,30分.解答应写出文字说明,证明过程或演算步骤.)
31.(本小题满分8分)已知a、b、c是△ABC中∠A、∠B、∠C的对边,S是△ABC的面积.若a=4,b=5,S=5,求c的长度.
32.(本小题满分10分)已知函数的定义域为R,求实数的取值范围。
33.(本小题满分12分)已知,且组成等差数列(为正偶数),又;
(1)求数列的通项;
(2)求的值;
(3) 比较的值与的大小,并说明理由.
河北省普通高中学业水平考试模拟试卷05答案
一.选择题
1 2 3 4 5 6 7 8 9 10 11 12 13
B A A A B C A C C D B A B
14 15 16 17 18 19 20 21 22 23 24 25
A A B B C C C B C A D C
1. 答案:B
解:tan300°+cot405°=tan(360°-60°)+cot(360°+45°)=-tan60°+cot45°=1-.
2.答案:A
解:根据子集的计算应有24-1=15(个).
3..答案:A
解:当a>1时,y=logax单调递增,y=a-x单调递减,故选A.
4.答案:A
解:已知向量,,,则与垂直,选A。
5.答案:B
解析:y=cos22x-sin22x=cos4x,T=.
6.答案:C
解:方程(x-1)2+y2=4表示以点(1,0)为圆心,2为半径的圆,x=a表示与x轴垂直且与圆相切的直线,而此时的切线方程分别为x=-1和x=3,由于a>0,取a=3.故选C.
7.答案:A
解:由可得选A。
8.答案:C
解:共有食品100种,抽取容量为20的样本,各抽取,故抽取植物油类与果蔬类食品种数之和为2+4=6,选C.
9.答案:C
解:由程序知,故选C 。
10.答案:D
解:正方体的三视图都相同,而三棱台的三视图各不相同,正确答案为D。
11.答案:B
解:由向量的减法知 选B.
12.答案:A
解:由已知得: sin(x-)≤0,所以2kπ+π≤x-≤2kπ+2π,2kπ+≤x≤2kπ+,令k=-1得-≤x≤,选A.
13.答案:B
解:由,所以.
14.答案:A
解:若两向量共线,则由于是非零向量,且,
则必有a=2b;代入可知只有A、C满足;若两向量不共线,
注意到向量模的几何意义,故可以构造如图所示的三角形,
使其满足OB=AB=BC;令a, b,则a-b,
∴a-2b且;
又BA+BC>AC ∴
∴,选A.
15.答案:A
解:因为Aa,即2RsinC>2RsinA.所以sinC>sinA.
16.答案:B
解:函数的反函数的定义域为原函数的值域,
原函数的值域为,∴ 选B。
17.答案:B
解:图中的图象所表示的函数当0≤x≤1时,它的解析式为,当1解析式为,∴解析式为(0≤x≤2)
18.答案:C
解:设前m项的和为b1,第m+1到2m项之和为b2,第2m+1到3m项之和为b3,则b1,b2,b3也成等差数列.
于是b1=30,b2=100-30=70,公差d=70-30=40.
∴b3=b2+d=70+40=110
∴前3m项之和S3m=b1+b2+b3=210.
19.答案:C
解:由KAB=KBC可得
20.答案:C
解:运用倒数法则,a>b,ab>0,②、④正确.又正数大于负数,故选C.
21.答案:B
解:联想到诱导公式及对同角三角函数公式解题
[
22.答案:C
解:[∵,且最大边长和最小边长是方程的两个根,则第三边为∴
]
23.答案:A
解:. 点P(m,n)的个数有36个,而满足题意的点有以下6个:(1,1),(1,2)(2,1)(1,3),(2,2),(3,1)
所求的概率为
24.答案:D
解:表示的可行域上的点与点的距离的平方值减1.
25.答案:C
解:]由,,故排除A;
由,,故排除B;
由,,故可确定方程的一个根位于下列区间(1.8,2.2),所以选择C
二.填空题
26.答案:
解析:由不等式得,解得
27.答案:2
解:由题意.
28.答案:4
解:设a1,a3,a11组成的等比数列公比为q.
∴a3=a1q=2q,a11=a1q2=2q2
又 ∵数列{an}是等差数列∴a11=a1+5(a3-a1)
∴2q2=a1+5(2q-a1) ∴2q2=2+5(2q-2),解得q=4
29.答案:2
解:圆心到直线的距离d==3
∴动点Q到直线距离的最小值为d-r=3-1=2
30.答案:
解:f(x)=sin2x-2cos2x-2=sin(2x-)-2,其中tan=.∴f(x)max=.
三.解答题
31.解:∵S=absinC,∴sinC=,于是∠C=60°或∠C=120°-----------3分
又∵c2=a2+b2-2abcosC,
当∠C=60°时,c2=a2+b2-ab,c= -------------5分
当∠C=120°时,c2=a2+b2+ab,c= -----------7分
∴c的长度为或 -------------------------8分
32.解:因为函数的定义域为R, 所以 恒成立, --------------1分
若,则,
当时,原不等式可化为,显然不合题意。
当时,原不等式可化为,恒成立。 --------3分
若,则依题意
------------------4分
解得 ----------------7分
所以 -------------9分
综上可知的取值范围是 ------------10分
33.解:(1)设数列的公差为d,
因为f(1)= a1+a2+a3+…+an=n2,则na1+d=n2,即2a1+(n-1)d=2n.
又f(-1)= -a1+a2-a3+…-an-1+an=n,即=n,d=2.解得a1=1. -------------3分
∴an=1+2(n-1)=2n-1. --------------5分
(2) =,把它两边都乘以,得:
两式相减,得:
= ----------7分
=
= -------------10分
(3)
∴ --------------12分
开始
是
否
输出
结束
①正方形
②圆锥
③三棱台
④正四棱锥
一、选择题:(本题共25小题,1-15小题每小题2分,16—25小题每小题3共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.tan300°+cot405°的值是
A.1+ B.1- C.-1- D.-1+
2.已知集合A={1,2,3,4},那么A的真子集的个数是
A.15 B.16 C.3 D.4
3.当a>1时,在同一坐标系中,函数y=a-x与y=logax的图象是
4.已知向量,,则与
A.垂直 B.不垂直也不平行 C.平行且同向 D.平行且反向
5.下列函数中,周期是的偶函数是
A.y=sin4x B.y=cos22x-sin22x
C.y=tan2x D.y=cos2x
6.已知直线x=a(a>0)和圆(x-1)2+y2=4相切,那么a的值是
A.5 B.4 C.3 D.2
7.在等比数列{an}中,a1=8,a4=64,,则公比q为
(A)2 (B)3 (C)4 (D)8
8.某商场有四类食品,其中粮食类、植物油类、动物性食品类及果蔬类分别有40种、10种、30种、20种,现从中抽取一个容量为20的样本进行食品安全检测。若采用分层抽样的方法抽取样本,则抽取的植物油类与果蔬类食品种数之和是
(A)4 (B)5 (C)6 (D)7
9.如果执行右面的程序框图,那么输出的
A.2450 B.2500 C.2550 D.2652
10.下列几何体各自的三视图中,有且仅有两个视图相同的
A.①② B.①③ C.①④ D.②④
11.若是不共线的任意三点,则以下各式中成立的是
A. B.
C. D.
12.使sinx≤cosx成立的x的一个变化区间是
A.[-,] B.[-,] C.[-,] D.[0,π]
13.在等比数列()中,若,,则该数列的前10项和为
A. B. C. D.
14.若非零向量、满足|一|=||,则
(A) |2|>|一2| (B) |2|<|一2|
(C) |2|>|2一| (D) |2|<|2一|
15.若A、B、C是△ABC的三个内角,且A
A. B. C. D.
17.图中的图象所表示的函数的解析式为
(A) (0≤x≤2)
(B) (0≤x≤2)
(C) (0≤x≤2)
(D) (0≤x≤2)
18.等差数列{an}的前m项和为30,前2m项和为100,则它的前3m项和为
A.130 B.170 C.210 D.260
19.下列多组点中,三点共线的是
A.(1,4),(-1,2),(3,5) B.(-2,-5),(7,6),(-5,3)
C.(1,0),(0,-),(7,2) D.(0,0),(2,4),(-1,3)
20.已知四个条件,①b>0>a ②0>a>b ③a>0>b ④a>b>0能推出成立的有
A.1个 B.2个 C.3个 D.4个
21.已知,则
A、2 B、-2 C、0 D、
22.在中,,且最大边长和最小边长是方程的两个根,则第三边的长为
A.2 B.3 C.4 D.5
23.连续掷两次骰子分别得到的点数为m、n,则点P(m,n)在直线x+y=5左下方的概率为
A. B. C. D.
24.已知满足约束条件,则的最小值是
A. B. C. D.
25.利用计算器,列出自变量和函数值的对应值如下表:
0.2 0.6 1.0 1.4 1.8 2.2 2.6 3.0 3.4 …
1.149 1.516 2.0 2.639 3.482 4.595 6.063 8.0 10.556 …
0.04 0.36 1.0 1.96 3.24 4.84 6.76 9.0 11.56 …
那么方程的一个根位于下列区间的
A.(0.6,1.0);B.(1.4,1.8);C.(1.8,2.2);D. (2.6,3.0)
二、填空题:(本题共5小题,每小题2分,共10分)
26.不等式的解集是___________
27.已知,则= .
28.等差数列{an}中,a1=2,公差不为零,且a1,a3,a11恰好是某等比数列的前三项,那么该等比数列公比的值等于 .
29.圆x2+y2-2x-2y+1=0上的动点Q到直线3x+4y+8=0距离的最小值为 .
30.函数f(x)=3sinxcosx-4cos2x的最大值是_____.
三、解答题:(本大题共3小题,30分.解答应写出文字说明,证明过程或演算步骤.)
31.(本小题满分8分)已知a、b、c是△ABC中∠A、∠B、∠C的对边,S是△ABC的面积.若a=4,b=5,S=5,求c的长度.
32.(本小题满分10分)已知函数的定义域为R,求实数的取值范围。
33.(本小题满分12分)已知,且组成等差数列(为正偶数),又;
(1)求数列的通项;
(2)求的值;
(3) 比较的值与的大小,并说明理由.
河北省普通高中学业水平考试模拟试卷05答案
一.选择题
1 2 3 4 5 6 7 8 9 10 11 12 13
B A A A B C A C C D B A B
14 15 16 17 18 19 20 21 22 23 24 25
A A B B C C C B C A D C
1. 答案:B
解:tan300°+cot405°=tan(360°-60°)+cot(360°+45°)=-tan60°+cot45°=1-.
2.答案:A
解:根据子集的计算应有24-1=15(个).
3..答案:A
解:当a>1时,y=logax单调递增,y=a-x单调递减,故选A.
4.答案:A
解:已知向量,,,则与垂直,选A。
5.答案:B
解析:y=cos22x-sin22x=cos4x,T=.
6.答案:C
解:方程(x-1)2+y2=4表示以点(1,0)为圆心,2为半径的圆,x=a表示与x轴垂直且与圆相切的直线,而此时的切线方程分别为x=-1和x=3,由于a>0,取a=3.故选C.
7.答案:A
解:由可得选A。
8.答案:C
解:共有食品100种,抽取容量为20的样本,各抽取,故抽取植物油类与果蔬类食品种数之和为2+4=6,选C.
9.答案:C
解:由程序知,故选C 。
10.答案:D
解:正方体的三视图都相同,而三棱台的三视图各不相同,正确答案为D。
11.答案:B
解:由向量的减法知 选B.
12.答案:A
解:由已知得: sin(x-)≤0,所以2kπ+π≤x-≤2kπ+2π,2kπ+≤x≤2kπ+,令k=-1得-≤x≤,选A.
13.答案:B
解:由,所以.
14.答案:A
解:若两向量共线,则由于是非零向量,且,
则必有a=2b;代入可知只有A、C满足;若两向量不共线,
注意到向量模的几何意义,故可以构造如图所示的三角形,
使其满足OB=AB=BC;令a, b,则a-b,
∴a-2b且;
又BA+BC>AC ∴
∴,选A.
15.答案:A
解:因为A
16.答案:B
解:函数的反函数的定义域为原函数的值域,
原函数的值域为,∴ 选B。
17.答案:B
解:图中的图象所表示的函数当0≤x≤1时,它的解析式为,当1
18.答案:C
解:设前m项的和为b1,第m+1到2m项之和为b2,第2m+1到3m项之和为b3,则b1,b2,b3也成等差数列.
于是b1=30,b2=100-30=70,公差d=70-30=40.
∴b3=b2+d=70+40=110
∴前3m项之和S3m=b1+b2+b3=210.
19.答案:C
解:由KAB=KBC可得
20.答案:C
解:运用倒数法则,a>b,ab>0,②、④正确.又正数大于负数,故选C.
21.答案:B
解:联想到诱导公式及对同角三角函数公式解题
[
22.答案:C
解:[∵,且最大边长和最小边长是方程的两个根,则第三边为∴
]
23.答案:A
解:. 点P(m,n)的个数有36个,而满足题意的点有以下6个:(1,1),(1,2)(2,1)(1,3),(2,2),(3,1)
所求的概率为
24.答案:D
解:表示的可行域上的点与点的距离的平方值减1.
25.答案:C
解:]由,,故排除A;
由,,故排除B;
由,,故可确定方程的一个根位于下列区间(1.8,2.2),所以选择C
二.填空题
26.答案:
解析:由不等式得,解得
27.答案:2
解:由题意.
28.答案:4
解:设a1,a3,a11组成的等比数列公比为q.
∴a3=a1q=2q,a11=a1q2=2q2
又 ∵数列{an}是等差数列∴a11=a1+5(a3-a1)
∴2q2=a1+5(2q-a1) ∴2q2=2+5(2q-2),解得q=4
29.答案:2
解:圆心到直线的距离d==3
∴动点Q到直线距离的最小值为d-r=3-1=2
30.答案:
解:f(x)=sin2x-2cos2x-2=sin(2x-)-2,其中tan=.∴f(x)max=.
三.解答题
31.解:∵S=absinC,∴sinC=,于是∠C=60°或∠C=120°-----------3分
又∵c2=a2+b2-2abcosC,
当∠C=60°时,c2=a2+b2-ab,c= -------------5分
当∠C=120°时,c2=a2+b2+ab,c= -----------7分
∴c的长度为或 -------------------------8分
32.解:因为函数的定义域为R, 所以 恒成立, --------------1分
若,则,
当时,原不等式可化为,显然不合题意。
当时,原不等式可化为,恒成立。 --------3分
若,则依题意
------------------4分
解得 ----------------7分
所以 -------------9分
综上可知的取值范围是 ------------10分
33.解:(1)设数列的公差为d,
因为f(1)= a1+a2+a3+…+an=n2,则na1+d=n2,即2a1+(n-1)d=2n.
又f(-1)= -a1+a2-a3+…-an-1+an=n,即=n,d=2.解得a1=1. -------------3分
∴an=1+2(n-1)=2n-1. --------------5分
(2) =,把它两边都乘以,得:
两式相减,得:
= ----------7分
=
= -------------10分
(3)
∴ --------------12分
开始
是
否
输出
结束
①正方形
②圆锥
③三棱台
④正四棱锥
同课章节目录
