人教版九年级数学上册 23.2.1 中心对称课件(28张ppt)
文档属性
| 名称 | 人教版九年级数学上册 23.2.1 中心对称课件(28张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-17 00:00:00 | ||
图片预览






文档简介
(共28张PPT)
图形的旋转
23
23.2.1
中心对称
课时目标
1.理解中心对称的概念。
2.掌握中心对称的性质并加以应用。
探究新知
中心对称的概念
【问题1】(1)如图,把其中一个图案绕点
O
旋转180°,你有什么发现?
两个图案能够完全重合在一起.
探究新知
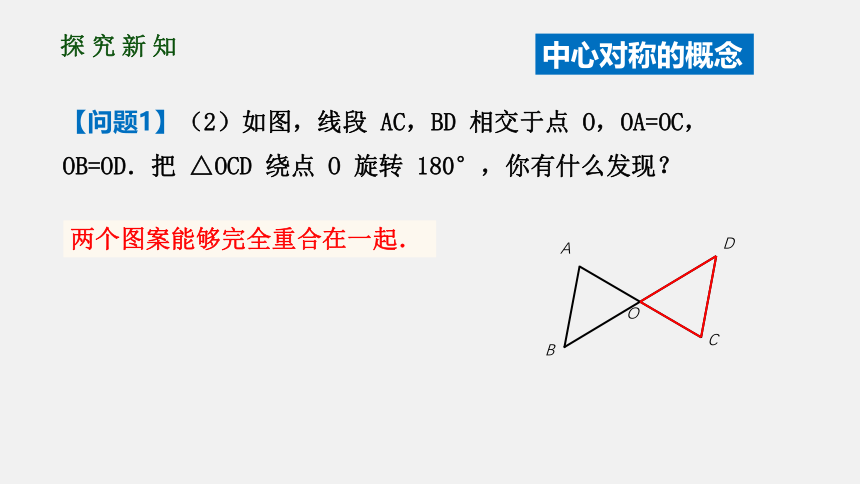
【问题1】(2)如图,线段
AC,BD
相交于点
O,OA=OC,OB=OD.把
△OCD
绕点
O
旋转
180°,你有什么发现?
中心对称的概念
两个图案能够完全重合在一起.
A
B
D
C
O
探究新知
【问题2】你能说说上述两个旋转的共同点吗?
(1)图形中旋转中心是哪一点?
(2)旋转的角度是多少?
(3)两个图形的关系?
中心对称的概念
(点
O
)
(180°)
(
重合
)
探究新知
像这样,把一个图形绕着某一点旋转
180°,
如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称.这个点叫做对称中心(简称中心)
这两个图形在旋转后能重合的对应点叫做关于对称中心的对称点.
中心对称的概念
探究新知
【问题3】中心对称与一般的旋转的联系和区别?
联系:中心对称和一般的旋转都是绕着某一点进行旋转;
区别:中心对称的旋转角度是180°,
一般的旋转的旋转角度不固定,中心对称是特殊的旋转.
中心对称的概念
探究新知
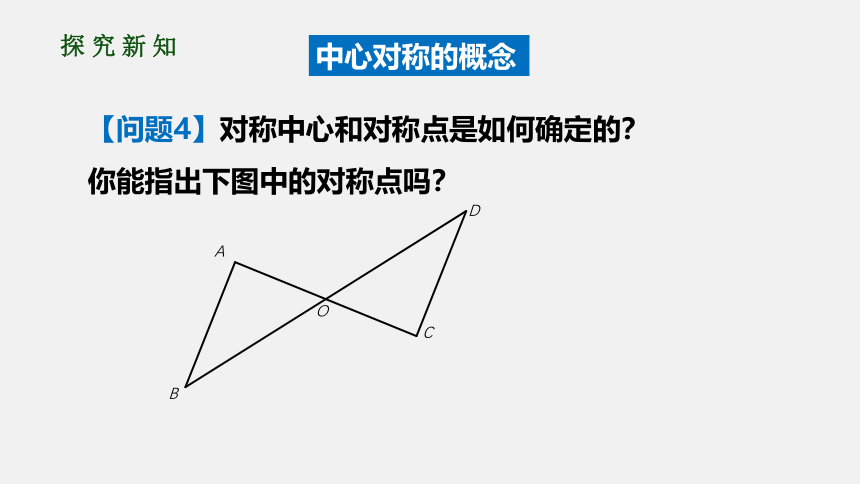
【问题4】对称中心和对称点是如何确定的?
你能指出下图中的对称点吗?
中心对称的概念
A
C
B
D
O
探究新知
C
A
B
C'
A′
B′
O
探究中心对称的性质
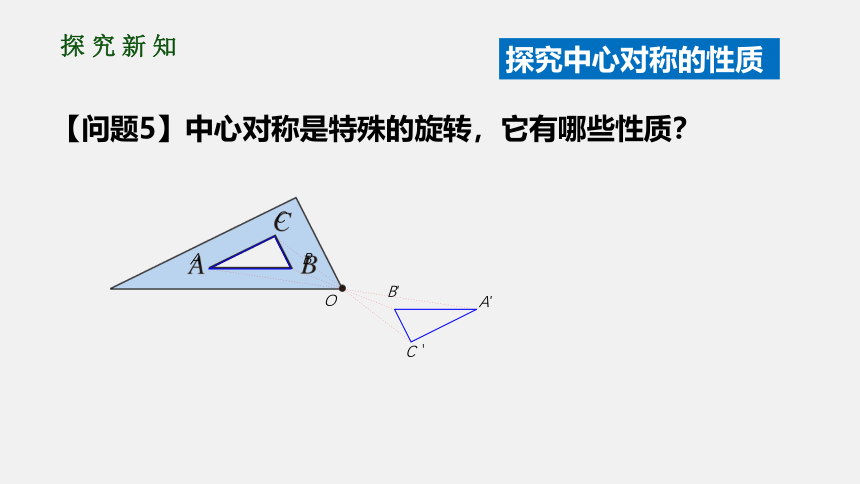
【问题5】中心对称是特殊的旋转,它有哪些性质?
探究新知
探究中心对称的性质
画好图形后思考:
(1)点
O
在线段
AA'上吗?如果在,在什么位置?
(2)△ABC
和△A'B'C'有什么关系?
(3)你能从这个探究中得到什么结论?
巩固练习
(1)中心对称的两个图形,
对称点所连线段都经过对称中心,
而且被对称中心所平分;
(2)中心对称的两个图形是全等图形.
探究中心对称的性质
反过来,如果两个图形的对应点连成的线段都经过某一点,
并且都被该点平分,那么这两个图形一定关于这一点成中心对称.
巩固练习
如图,四边形ABCD与四边形A1B1C1D1成中心对称吗?
若是,请指明对称中心,并回答问题:
(1)点A的对称点是
,点B的对称点是
.
(2)点A,O,A1三点共线吗?若是,还有其他三点共线吗?
点A1
点B1
A,O,A1三点共线,还有B,O,B1;C,O,C1;D,O,D1三点共线;
根据中心对称的性质
及识别方法
可知,四边形ABCD与四边形
A1B1C1D1关于点O成中心对称,
其对称中心是点O.
巩固练习
(3)指明图中相等的线段.
图中相等的线段有:
OA=OA1,OB=OB1,OC=OC1,OD=OD1,
AB=A1B1,BC=B1C1,CD=C1D1,DA=D1A1.
巩固练习
你用什么方法识别两个图形是否关于某点中心对称?
A'
C
C'
A
B
B'
巩固练习
【方法2】如果两个图形的对应点连成的线段都经过某一点,并且都被该点平分,那么这两个图形一定关于这一点成中心对称.
【方法1】将其中一个图形绕某一点旋转180°
如果能够与另一个完全重合,那么它们关于这一点中心对称;
巩固练习
1.点的中心对称点的作法
A
A′
B′
B
O
2.线段的中心对称线段的作法
A
O
A′
以点O为对称中心,作出点A的对称点A′;
以点O为对称中心,作出线段AB的对称线段点A′B′
点A′即为所求的点
应用中心对称性质画图
巩固练习
【例1】(2)如右图,选择点
O
为对称中心,画出与△ABC关于点
O
对称的△A'B'C
.
解:
A′
C′
B′
△A′B′C′即为所求的三角形
巩固练习
如图,已知△A
B
C
与△A'B'C'中心对称,
求出它们的对称中心O.
A
B
C
A'
B'
C'
巩固练习
【解法一】根据观察,B,B'应是对应点,连接BB',
用刻度尺找出BB'的中点O,则点O即为所求(如图)
A
B
C
A'
B'
C'
O
巩固练习
O
【解法二】根据观察,B,B'及C,C'应是两组对应点,连接BB',CC',BB',CC'相交于点O,则点O即为所求.
A
B
C
A'
B'
C'
巩固练习
轴对称与中心对称定义、性质对比图:
轴对称
中心对称
定
义
①有一条对称轴—直线
②图形沿轴对折(翻转达180°)
③翻转后与另一个图形重合
①有一个对称中心—点
②图形绕中心旋转180°
③旋转后与另一个图形重合
性
质
①两个图形是全等形
②对称轴是对称点连线的垂直平分线
①两个图形是全等形
②对称点连线都过对称中心,
且被对称中心平分
巩固练习
轴
对
称
中心对称
1
有一条对称轴
——
直线
有一个对称中心
——
点
2
图形沿轴对折(翻转
180°
)
图形绕中心旋转
180°
3
翻转后和另一个图形重合
旋转后和另一个图形重合
A
B
C
C
1
A
1
B
1
O
1.
已知下列命题:①
关于中心对称的两个图形不一定全等;②关于中心对称的两个图形一定全等;③两个全等的图形一定成中心对称,其中假命题的个数是(
)
A.
0 B.
1 C.
2 D.
3
巩固练习
C
巩固练习
2.
若线段AB与线段CD(与AB不在同一直线上)关于点O
中心对称,则AB和CD的关系是(
)
A.
AB=CD
B.
AB∥CD
C.
平行且相等
D.
不确定
C
巩固练习
2.如图,△AOB与△DOC是成中心对称的两个图形,对称中心是
,点B,A对称点分别是
,相等线段有
AO=
,BO=
,CD=
.
点O
点C,
D
DO
CO
AB
巩固练习
3.如图,将一张直角三角形纸片ABC沿中位线D
E剪开后,在平面上将△BDE绕着CB的中点D逆时针旋转180°,点E
到了点E′位置,则四边形ACE′E
的形状是
.
平行四边形
巩固练习
4.若△ABC与△DEF关于点O成中心对称,且A,B,C的对称点分别为D,E,F,若AB=5,AC=3,则EF的范围是
.
2<EF<8
(1)本节课学了哪些主要内容?
(2)怎样画一个图形关于一个点的对称图形?
课堂小结
图形的旋转
23
23.2.1
中心对称
课时目标
1.理解中心对称的概念。
2.掌握中心对称的性质并加以应用。
探究新知
中心对称的概念
【问题1】(1)如图,把其中一个图案绕点
O
旋转180°,你有什么发现?
两个图案能够完全重合在一起.
探究新知
【问题1】(2)如图,线段
AC,BD
相交于点
O,OA=OC,OB=OD.把
△OCD
绕点
O
旋转
180°,你有什么发现?
中心对称的概念
两个图案能够完全重合在一起.
A
B
D
C
O
探究新知
【问题2】你能说说上述两个旋转的共同点吗?
(1)图形中旋转中心是哪一点?
(2)旋转的角度是多少?
(3)两个图形的关系?
中心对称的概念
(点
O
)
(180°)
(
重合
)
探究新知
像这样,把一个图形绕着某一点旋转
180°,
如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称.这个点叫做对称中心(简称中心)
这两个图形在旋转后能重合的对应点叫做关于对称中心的对称点.
中心对称的概念
探究新知
【问题3】中心对称与一般的旋转的联系和区别?
联系:中心对称和一般的旋转都是绕着某一点进行旋转;
区别:中心对称的旋转角度是180°,
一般的旋转的旋转角度不固定,中心对称是特殊的旋转.
中心对称的概念
探究新知
【问题4】对称中心和对称点是如何确定的?
你能指出下图中的对称点吗?
中心对称的概念
A
C
B
D
O
探究新知
C
A
B
C'
A′
B′
O
探究中心对称的性质
【问题5】中心对称是特殊的旋转,它有哪些性质?
探究新知
探究中心对称的性质
画好图形后思考:
(1)点
O
在线段
AA'上吗?如果在,在什么位置?
(2)△ABC
和△A'B'C'有什么关系?
(3)你能从这个探究中得到什么结论?
巩固练习
(1)中心对称的两个图形,
对称点所连线段都经过对称中心,
而且被对称中心所平分;
(2)中心对称的两个图形是全等图形.
探究中心对称的性质
反过来,如果两个图形的对应点连成的线段都经过某一点,
并且都被该点平分,那么这两个图形一定关于这一点成中心对称.
巩固练习
如图,四边形ABCD与四边形A1B1C1D1成中心对称吗?
若是,请指明对称中心,并回答问题:
(1)点A的对称点是
,点B的对称点是
.
(2)点A,O,A1三点共线吗?若是,还有其他三点共线吗?
点A1
点B1
A,O,A1三点共线,还有B,O,B1;C,O,C1;D,O,D1三点共线;
根据中心对称的性质
及识别方法
可知,四边形ABCD与四边形
A1B1C1D1关于点O成中心对称,
其对称中心是点O.
巩固练习
(3)指明图中相等的线段.
图中相等的线段有:
OA=OA1,OB=OB1,OC=OC1,OD=OD1,
AB=A1B1,BC=B1C1,CD=C1D1,DA=D1A1.
巩固练习
你用什么方法识别两个图形是否关于某点中心对称?
A'
C
C'
A
B
B'
巩固练习
【方法2】如果两个图形的对应点连成的线段都经过某一点,并且都被该点平分,那么这两个图形一定关于这一点成中心对称.
【方法1】将其中一个图形绕某一点旋转180°
如果能够与另一个完全重合,那么它们关于这一点中心对称;
巩固练习
1.点的中心对称点的作法
A
A′
B′
B
O
2.线段的中心对称线段的作法
A
O
A′
以点O为对称中心,作出点A的对称点A′;
以点O为对称中心,作出线段AB的对称线段点A′B′
点A′即为所求的点
应用中心对称性质画图
巩固练习
【例1】(2)如右图,选择点
O
为对称中心,画出与△ABC关于点
O
对称的△A'B'C
.
解:
A′
C′
B′
△A′B′C′即为所求的三角形
巩固练习
如图,已知△A
B
C
与△A'B'C'中心对称,
求出它们的对称中心O.
A
B
C
A'
B'
C'
巩固练习
【解法一】根据观察,B,B'应是对应点,连接BB',
用刻度尺找出BB'的中点O,则点O即为所求(如图)
A
B
C
A'
B'
C'
O
巩固练习
O
【解法二】根据观察,B,B'及C,C'应是两组对应点,连接BB',CC',BB',CC'相交于点O,则点O即为所求.
A
B
C
A'
B'
C'
巩固练习
轴对称与中心对称定义、性质对比图:
轴对称
中心对称
定
义
①有一条对称轴—直线
②图形沿轴对折(翻转达180°)
③翻转后与另一个图形重合
①有一个对称中心—点
②图形绕中心旋转180°
③旋转后与另一个图形重合
性
质
①两个图形是全等形
②对称轴是对称点连线的垂直平分线
①两个图形是全等形
②对称点连线都过对称中心,
且被对称中心平分
巩固练习
轴
对
称
中心对称
1
有一条对称轴
——
直线
有一个对称中心
——
点
2
图形沿轴对折(翻转
180°
)
图形绕中心旋转
180°
3
翻转后和另一个图形重合
旋转后和另一个图形重合
A
B
C
C
1
A
1
B
1
O
1.
已知下列命题:①
关于中心对称的两个图形不一定全等;②关于中心对称的两个图形一定全等;③两个全等的图形一定成中心对称,其中假命题的个数是(
)
A.
0 B.
1 C.
2 D.
3
巩固练习
C
巩固练习
2.
若线段AB与线段CD(与AB不在同一直线上)关于点O
中心对称,则AB和CD的关系是(
)
A.
AB=CD
B.
AB∥CD
C.
平行且相等
D.
不确定
C
巩固练习
2.如图,△AOB与△DOC是成中心对称的两个图形,对称中心是
,点B,A对称点分别是
,相等线段有
AO=
,BO=
,CD=
.
点O
点C,
D
DO
CO
AB
巩固练习
3.如图,将一张直角三角形纸片ABC沿中位线D
E剪开后,在平面上将△BDE绕着CB的中点D逆时针旋转180°,点E
到了点E′位置,则四边形ACE′E
的形状是
.
平行四边形
巩固练习
4.若△ABC与△DEF关于点O成中心对称,且A,B,C的对称点分别为D,E,F,若AB=5,AC=3,则EF的范围是
.
2<EF<8
(1)本节课学了哪些主要内容?
(2)怎样画一个图形关于一个点的对称图形?
课堂小结
同课章节目录
