人教版九年级数学上册 23.2.2 中心对称图形课件(40张ppt)
文档属性
| 名称 | 人教版九年级数学上册 23.2.2 中心对称图形课件(40张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-17 00:00:00 | ||
图片预览








文档简介
(共40张PPT)
图形的旋转
23
23.2.2
中心对称图形
课时目标
1.了解中心对称图形及其堆成中心的概念,
掌握这两个概念的应用。
2.会区别成中心对称的两个图形与中心对称图形。
探究新知
【1】如图,将线段
AB
绕它的中点旋转
180°,你有什么发现?
A
B
可以发现:线段
AB
绕它的中点旋转
180°后与它本身重合
探究新知
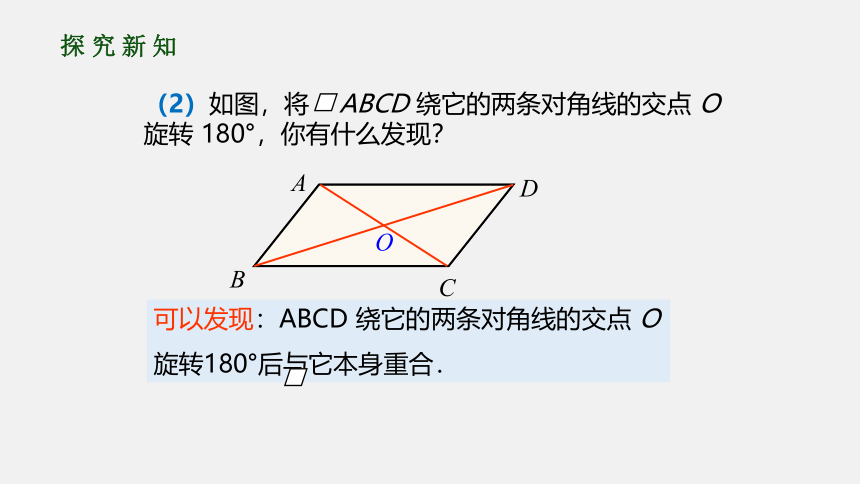
(2)如图,将
ABCD
绕它的两条对角线的交点
O
旋转
180°,你有什么发现?
A
B
C
D
可以发现:ABCD
绕它的两条对角线的交点
O
旋转180°后与它本身重合.
O
探究新知
A
B
B
D
O
O
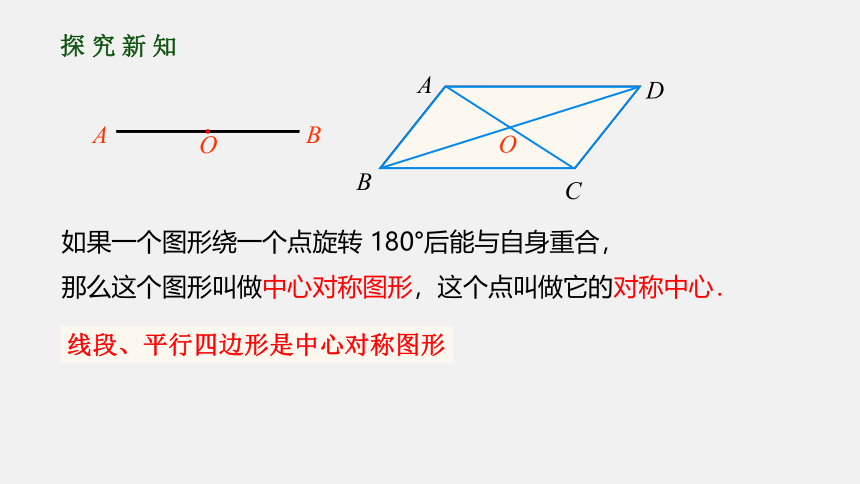
线段、平行四边形是中心对称图形
如果一个图形绕一个点旋转
180°后能与自身重合,
那么这个图形叫做中心对称图形,这个点叫做它的对称中心.
A
C
探究新知
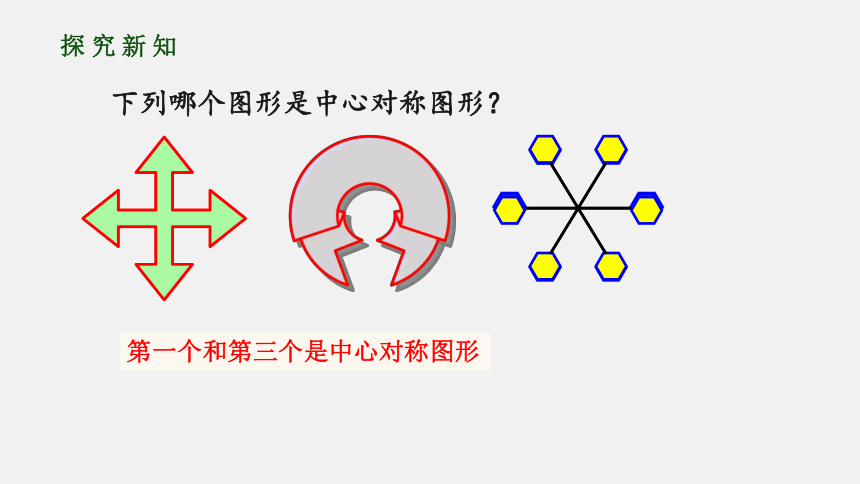
下列哪个图形是中心对称图形?
第一个和第三个是中心对称图形
探究新知
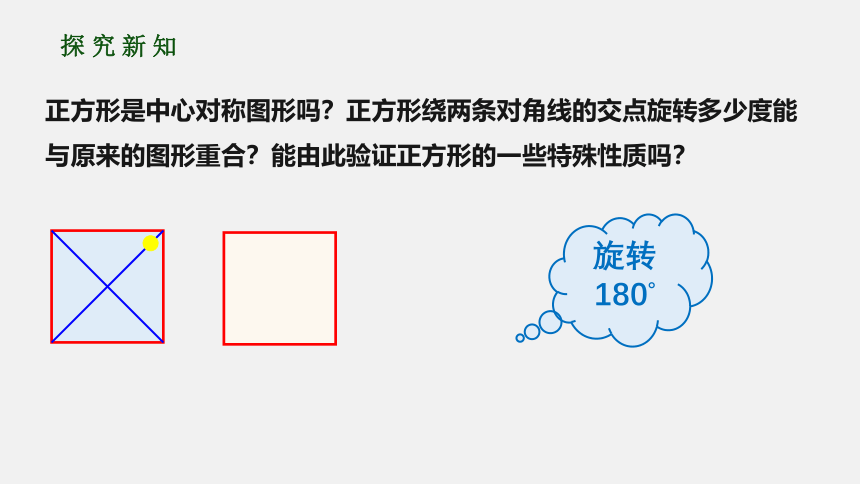
【1】正方形是中心对称图形吗?正方形绕两条对角线的交点旋转多少度能与原来的图形重合?能由此验证正方形的一些特殊性质吗?
旋转90°
探究新知
正方形是中心对称图形吗?正方形绕两条对角线的交点旋转多少度能与原来的图形重合?能由此验证正方形的一些特殊性质吗?
旋转180°
探究新知
正方形是中心对称图形吗?正方形绕两条对角线的交点旋转多少度能与原来的图形重合?能由此验证正方形的一些特殊性质吗?
旋转270°
探究新知
正方形是中心对称图形吗?正方形绕两条对角线的交点旋转多少度能与原来的图形重合?能由此验证正方形的一些特殊性质吗?
旋转360°
探究新知
正方形是中心对称图形吗?正方形绕两条对角线的交点旋转多少度能与原来的图形重合?能由此验证正方形的一些特殊性质吗?
旋转nx900
探究新知
正方形是中心对称图形;它绕两条对角线的交点旋转900或其整数倍,都能与原来的图形重合,因此,可以验证正方形的四边相等、四角相等、对角线互相垂直平分等性质。
巩固练习
正三角形是中心对称图形吗?
正方形呢?正五边形呢?正六边形呢?……你能发现什么规律?
边数为偶数的正多边形都是中心对称图形。
√
×
√
×
巩固练习
如图,点O是正六边形ABCDEF的中心.
A
F
E
D
C
B
直线AD,BE,CF以及AB,BC,CD的垂直平分线都是这个正六边形的对称轴.
60°或其整数倍.
巩固练习
如图,点O是正六边形ABCDEF的中心.
(1)找出这个轴对称图形的对称轴.
(2)这个正六边形绕点O旋转多少度后和原来的图形重合?
(3)如果换成其他的正多边形呢?能得到一般的结论吗?
一般地,绕正n边形的中心旋转3600/n或其整数倍都能与原来的图形重合.
巩固练习
下列所述图形中,既是中心对称图形,又是轴对称图形的是(
)
A.
矩形
B.
平行四边形
C.
正五边形
D.
正三角形
A
巩固练习
名 称
定 义
区 别
联 系
旋转对称图形
如果一个图形绕着某一点旋转一定角度(小于周角)后能与原图形完全重合,那么这个图形叫做旋转对称图形
旋转角度不一定是180°
只有旋转180°与原图形重合的旋转对称图形才是中心对称图形,而中心对称图形一定是旋转对称图形
中心对称图形
如果一个图形绕某点旋转180°后能与原图形重合,那么这个图形叫做中心对称图形
必须旋转180°
(1)中心对称图形与旋转对称图形的比较
名 称
定 义
基本图形
区
别
举 例
中心对
称图形
如果一个图形绕某点旋转180°后能与原图形重合,那么这个图形叫做中心对称图形
绕某一点旋转180°
线段、平行四边形、矩形、菱形
轴对称
图形
如果一个图形沿某一条直线翻折180°后,直线两旁的部分能够互相重合,那么这样的图形叫做轴对称图形
沿某一条直线翻折180°(对折)
线段、等腰三角形、矩形、菱形、正方形、圆
巩固练习
(2)中心对称图形与轴对称图形的比较
巩固练习
(3)中心对称与中心对称图形的比较
【中心对称】把一个图形绕着某一个点旋转180?,如果它能够与另一个图形重合,那么就说这两个图形关于这点对称,这个点叫做对称中心,两个图形关于点对称也称中心对称,这两个图形中的对应点叫做关于中心的对称点。
巩固练习
(3)中心对称与中心对称图形的比较
性质
①两个图形完全重合;
②对应点连线都经过对称中心,并且被对称中心平分
区别
①两个图形的关系
②对称点在两个图形上
联系:若把中心对称图形的两部分分别看作两图,则它们成中心对称;
若把中心对称的两图看作一个整体,
则成为中心对称图形.
巩固练习
(3)中心对称与中心对称图形的比较
性质
如果一个图形绕着一个点旋转180?后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心。
区别
①具有某种性质的一个图形
②对称点在一个图形上
联系:若把中心对称图形的两部分分别看作两图,则它们成中心对称;
若把中心对称的两图看作一个整体,
则成为中心对称图形.
中心对称图形
巩固练习
如图所示,方格纸中的每个小正方形的边长均为1.
(1)观察图甲、乙中所画的“L”型图形,然后各补画一个小正方形,
使图甲中所成的图形是轴对称图形,图乙中所成的图形是中心对称图形;
(2)补画后,图甲、乙中的图形是不是正方体的表面展开图?
巩固练习
(1)观察图甲、乙中所画的“L”型图形,然后各补画一个小正方形,使图甲中所成的图
形是轴对称图形,图乙中所成的图形是中心对称图形
(2)补画后,图甲、乙中的图形是不是正方体的表面展开图?
巩固练习
解(1)如图所示.(2)图甲①不是,图甲②是,图乙是.
巩固练习
1.
下列图形中既是轴对称图形又是中心对称图形的是(
)
A
巩固练习
A
2.
下列图形中,既是轴对称图形,又是中心对称图形的是(
)
3.
晋商大院的许多窗格图案蕴含着对称之美,现从中选取以下四种窗格图案,其中是中心对称图形但不是轴对称图形的是(
)
巩固练习
B
巩固练习
(1)下列图形中即是轴对称图形又是中心对称图形的是(
)
A.
角
B.
等边三角形
C.
线段
D.
平行四边形
C
(2)下列多边形中,是中心对称图形而不是轴对称图形的是(
)
A.
平行四边形
B.
矩形
C.
菱形
D.
正方形
A
(3)
如图,中心对称图形有(
)
巩固练习
C
A.1个
B.2个
C.3个
D.4个
巩固练习
(4)下列四个图形中,是中心对称图形的为(
)
C
巩固练习
判断下列说法是否正确。
(1)轴对称图形也是中心对称图形.(
)
(2)旋转对称图形也是中心对称图形.(
)
(3)平行四边形、长方形和正方形都是中心对称图形,对角线的交点是它们的对称中心.(
)
(4)角是轴对称图形也是中心对称图形.(
)
(5)在成中心对称的两个图形中,对应线段平行(或在同一直线上)且相等.
(
)
×
√
×
√
×
巩固练习
判断下列图形是否是中心对称图形?
√
×
√
√
√
√
√
√
巩固练习
√
×
√
×
√
巩固练习
√
×
×
√
√
√
√
√
√
√
(1)哪些只是轴对称图形?
(2)哪些只是中心对称图形?
(3)哪些既是轴对称图形,又是中心对称图形?
巩固练习
观察图形,并回答下面的问题:
(3)(4)(6)
(1)
(2)(5)
(1)
(3)
(2)
(4)
(5)
(6)
巩固练习
在①线段、
②角、
③等腰三角形、
④等腰梯形、⑤平行四边形、
⑥矩形、
⑦菱形、
⑧正方形和⑨圆中,是轴对称图形的有_____________________,是中心对称图形的有_______________,既是轴对称图形又是中心对称图形的有____________.
①⑤⑥⑦⑧⑨
①②③④⑥⑦⑧⑨
①⑥⑦⑧⑨
巩固练习
下面的扑克牌中,哪些牌面是中心对称图形?
√
√
√
巩固练习
在圆、平行四边形、矩形、菱形、正方形、等腰三角形六种图形中,是中心对称图形但不是轴对称图形的是
.
平行四边形
巩固练习
在下列艺术字
,
其中既是轴对称图形又是中心对称图形的有
个.
1
课堂小结
(1)本节课学了哪些主要内容?
(2)中心对称图形和两个图形成中心对称的联系与区别?
图形的旋转
23
23.2.2
中心对称图形
课时目标
1.了解中心对称图形及其堆成中心的概念,
掌握这两个概念的应用。
2.会区别成中心对称的两个图形与中心对称图形。
探究新知
【1】如图,将线段
AB
绕它的中点旋转
180°,你有什么发现?
A
B
可以发现:线段
AB
绕它的中点旋转
180°后与它本身重合
探究新知
(2)如图,将
ABCD
绕它的两条对角线的交点
O
旋转
180°,你有什么发现?
A
B
C
D
可以发现:ABCD
绕它的两条对角线的交点
O
旋转180°后与它本身重合.
O
探究新知
A
B
B
D
O
O
线段、平行四边形是中心对称图形
如果一个图形绕一个点旋转
180°后能与自身重合,
那么这个图形叫做中心对称图形,这个点叫做它的对称中心.
A
C
探究新知
下列哪个图形是中心对称图形?
第一个和第三个是中心对称图形
探究新知
【1】正方形是中心对称图形吗?正方形绕两条对角线的交点旋转多少度能与原来的图形重合?能由此验证正方形的一些特殊性质吗?
旋转90°
探究新知
正方形是中心对称图形吗?正方形绕两条对角线的交点旋转多少度能与原来的图形重合?能由此验证正方形的一些特殊性质吗?
旋转180°
探究新知
正方形是中心对称图形吗?正方形绕两条对角线的交点旋转多少度能与原来的图形重合?能由此验证正方形的一些特殊性质吗?
旋转270°
探究新知
正方形是中心对称图形吗?正方形绕两条对角线的交点旋转多少度能与原来的图形重合?能由此验证正方形的一些特殊性质吗?
旋转360°
探究新知
正方形是中心对称图形吗?正方形绕两条对角线的交点旋转多少度能与原来的图形重合?能由此验证正方形的一些特殊性质吗?
旋转nx900
探究新知
正方形是中心对称图形;它绕两条对角线的交点旋转900或其整数倍,都能与原来的图形重合,因此,可以验证正方形的四边相等、四角相等、对角线互相垂直平分等性质。
巩固练习
正三角形是中心对称图形吗?
正方形呢?正五边形呢?正六边形呢?……你能发现什么规律?
边数为偶数的正多边形都是中心对称图形。
√
×
√
×
巩固练习
如图,点O是正六边形ABCDEF的中心.
A
F
E
D
C
B
直线AD,BE,CF以及AB,BC,CD的垂直平分线都是这个正六边形的对称轴.
60°或其整数倍.
巩固练习
如图,点O是正六边形ABCDEF的中心.
(1)找出这个轴对称图形的对称轴.
(2)这个正六边形绕点O旋转多少度后和原来的图形重合?
(3)如果换成其他的正多边形呢?能得到一般的结论吗?
一般地,绕正n边形的中心旋转3600/n或其整数倍都能与原来的图形重合.
巩固练习
下列所述图形中,既是中心对称图形,又是轴对称图形的是(
)
A.
矩形
B.
平行四边形
C.
正五边形
D.
正三角形
A
巩固练习
名 称
定 义
区 别
联 系
旋转对称图形
如果一个图形绕着某一点旋转一定角度(小于周角)后能与原图形完全重合,那么这个图形叫做旋转对称图形
旋转角度不一定是180°
只有旋转180°与原图形重合的旋转对称图形才是中心对称图形,而中心对称图形一定是旋转对称图形
中心对称图形
如果一个图形绕某点旋转180°后能与原图形重合,那么这个图形叫做中心对称图形
必须旋转180°
(1)中心对称图形与旋转对称图形的比较
名 称
定 义
基本图形
区
别
举 例
中心对
称图形
如果一个图形绕某点旋转180°后能与原图形重合,那么这个图形叫做中心对称图形
绕某一点旋转180°
线段、平行四边形、矩形、菱形
轴对称
图形
如果一个图形沿某一条直线翻折180°后,直线两旁的部分能够互相重合,那么这样的图形叫做轴对称图形
沿某一条直线翻折180°(对折)
线段、等腰三角形、矩形、菱形、正方形、圆
巩固练习
(2)中心对称图形与轴对称图形的比较
巩固练习
(3)中心对称与中心对称图形的比较
【中心对称】把一个图形绕着某一个点旋转180?,如果它能够与另一个图形重合,那么就说这两个图形关于这点对称,这个点叫做对称中心,两个图形关于点对称也称中心对称,这两个图形中的对应点叫做关于中心的对称点。
巩固练习
(3)中心对称与中心对称图形的比较
性质
①两个图形完全重合;
②对应点连线都经过对称中心,并且被对称中心平分
区别
①两个图形的关系
②对称点在两个图形上
联系:若把中心对称图形的两部分分别看作两图,则它们成中心对称;
若把中心对称的两图看作一个整体,
则成为中心对称图形.
巩固练习
(3)中心对称与中心对称图形的比较
性质
如果一个图形绕着一个点旋转180?后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心。
区别
①具有某种性质的一个图形
②对称点在一个图形上
联系:若把中心对称图形的两部分分别看作两图,则它们成中心对称;
若把中心对称的两图看作一个整体,
则成为中心对称图形.
中心对称图形
巩固练习
如图所示,方格纸中的每个小正方形的边长均为1.
(1)观察图甲、乙中所画的“L”型图形,然后各补画一个小正方形,
使图甲中所成的图形是轴对称图形,图乙中所成的图形是中心对称图形;
(2)补画后,图甲、乙中的图形是不是正方体的表面展开图?
巩固练习
(1)观察图甲、乙中所画的“L”型图形,然后各补画一个小正方形,使图甲中所成的图
形是轴对称图形,图乙中所成的图形是中心对称图形
(2)补画后,图甲、乙中的图形是不是正方体的表面展开图?
巩固练习
解(1)如图所示.(2)图甲①不是,图甲②是,图乙是.
巩固练习
1.
下列图形中既是轴对称图形又是中心对称图形的是(
)
A
巩固练习
A
2.
下列图形中,既是轴对称图形,又是中心对称图形的是(
)
3.
晋商大院的许多窗格图案蕴含着对称之美,现从中选取以下四种窗格图案,其中是中心对称图形但不是轴对称图形的是(
)
巩固练习
B
巩固练习
(1)下列图形中即是轴对称图形又是中心对称图形的是(
)
A.
角
B.
等边三角形
C.
线段
D.
平行四边形
C
(2)下列多边形中,是中心对称图形而不是轴对称图形的是(
)
A.
平行四边形
B.
矩形
C.
菱形
D.
正方形
A
(3)
如图,中心对称图形有(
)
巩固练习
C
A.1个
B.2个
C.3个
D.4个
巩固练习
(4)下列四个图形中,是中心对称图形的为(
)
C
巩固练习
判断下列说法是否正确。
(1)轴对称图形也是中心对称图形.(
)
(2)旋转对称图形也是中心对称图形.(
)
(3)平行四边形、长方形和正方形都是中心对称图形,对角线的交点是它们的对称中心.(
)
(4)角是轴对称图形也是中心对称图形.(
)
(5)在成中心对称的两个图形中,对应线段平行(或在同一直线上)且相等.
(
)
×
√
×
√
×
巩固练习
判断下列图形是否是中心对称图形?
√
×
√
√
√
√
√
√
巩固练习
√
×
√
×
√
巩固练习
√
×
×
√
√
√
√
√
√
√
(1)哪些只是轴对称图形?
(2)哪些只是中心对称图形?
(3)哪些既是轴对称图形,又是中心对称图形?
巩固练习
观察图形,并回答下面的问题:
(3)(4)(6)
(1)
(2)(5)
(1)
(3)
(2)
(4)
(5)
(6)
巩固练习
在①线段、
②角、
③等腰三角形、
④等腰梯形、⑤平行四边形、
⑥矩形、
⑦菱形、
⑧正方形和⑨圆中,是轴对称图形的有_____________________,是中心对称图形的有_______________,既是轴对称图形又是中心对称图形的有____________.
①⑤⑥⑦⑧⑨
①②③④⑥⑦⑧⑨
①⑥⑦⑧⑨
巩固练习
下面的扑克牌中,哪些牌面是中心对称图形?
√
√
√
巩固练习
在圆、平行四边形、矩形、菱形、正方形、等腰三角形六种图形中,是中心对称图形但不是轴对称图形的是
.
平行四边形
巩固练习
在下列艺术字
,
其中既是轴对称图形又是中心对称图形的有
个.
1
课堂小结
(1)本节课学了哪些主要内容?
(2)中心对称图形和两个图形成中心对称的联系与区别?
同课章节目录
