人教版七年级数学下册课件:5.1相交线(共25张PPT)
文档属性
| 名称 | 人教版七年级数学下册课件:5.1相交线(共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 161.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-17 15:24:25 | ||
图片预览







文档简介
(共25张PPT)
七年级下册数学
第五章相交线与平行线
5.1
相交线
巩固与提高
知识点1:相交线
知识点2:对顶角、邻补角
知识点3:垂线
知识点4:垂线段最短
知识点5:点到直线的距离
知识点6:同位角、内错角、同旁内角
知识点1:相交线
(1)相交线的定义
两条直线交于一点,我们称这两条直线相交.相对的,我们称这两条直线为相交线.
(2)两条相交线在形成的角中有特殊的数量关系和位置关系的有对顶角和邻补角两类.
(3)在同一平面内,两条直线的位置关系有两种:平行和相交(重合除外).
例1.平面内两两相交的6条直线,其交点个数最少为
个,最多为
个,n条直线两两相交的直线最多有
个交点。
1
15
解:根据题意可得:6条直线相交于一点时交点最少,此时交点为1个;
若平面内有相交的2条直线,则最多有1个交点;(即:1=
=1);
若平面内有两两相交的3条直线,则最多有3个交点;(即:1+2=
=3);
若平面内有两两相交的4条直线,则最多有6个交点;(即:1+2+3=
=6);
若平面内有两两相交的5条直线,则最多有10个交点;
(即:1+2+3+4=
=10);
则平面内两两相交的6条直线,其交点个数最多有15个交点;
(即1+2+3+4+5=
=15);
若平面内有n条直线两两相交,则最多有
个交点;
知识点2:对顶角、邻补角
(1)对顶角:有一个公共顶点,并且一个角的两边分别是另一个角的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.
(2)邻补角:只有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角.
(3)对顶角的性质:对顶角相等.
(4)邻补角的性质:邻补角互补,即和为180°.
(5)邻补角、对顶角成对出现,在相交直线中,一个角的邻补角有两个.邻补角、对顶角都是相对与两个角而言,是指的两个角的一种位置关系.它们都是在两直线相交的前提下形成的.
PART
01
工作概述
PART
04
未来展望
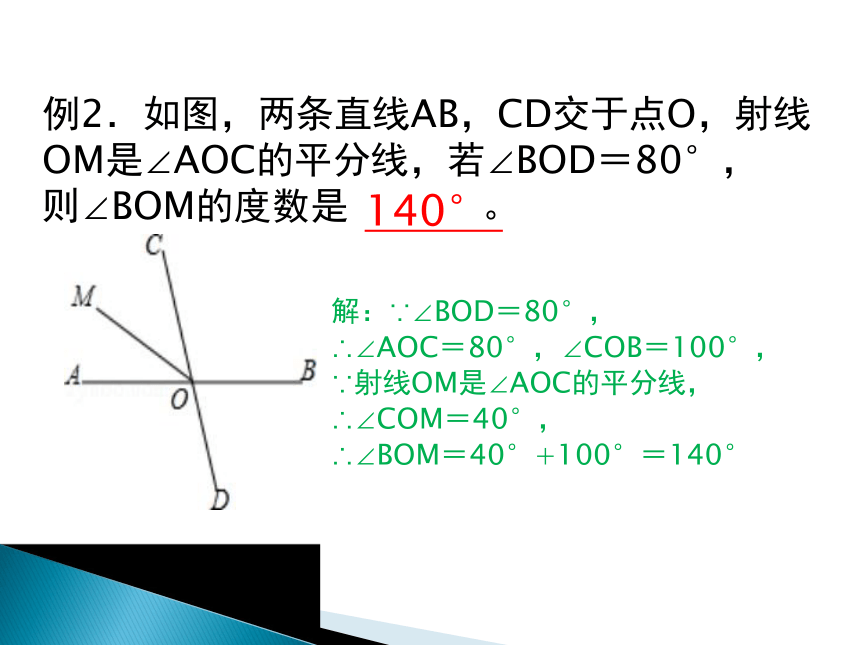
例2.如图,两条直线AB,CD交于点O,射线OM是∠AOC的平分线,若∠BOD=80°,
则∠BOM的度数是
。
解:∵∠BOD=80°,
∴∠AOC=80°,∠COB=100°,
∵射线OM是∠AOC的平分线,
∴∠COM=40°,
∴∠BOM=40°+100°=140°
140°
PART
01
工作概述
PART
04
未来展望
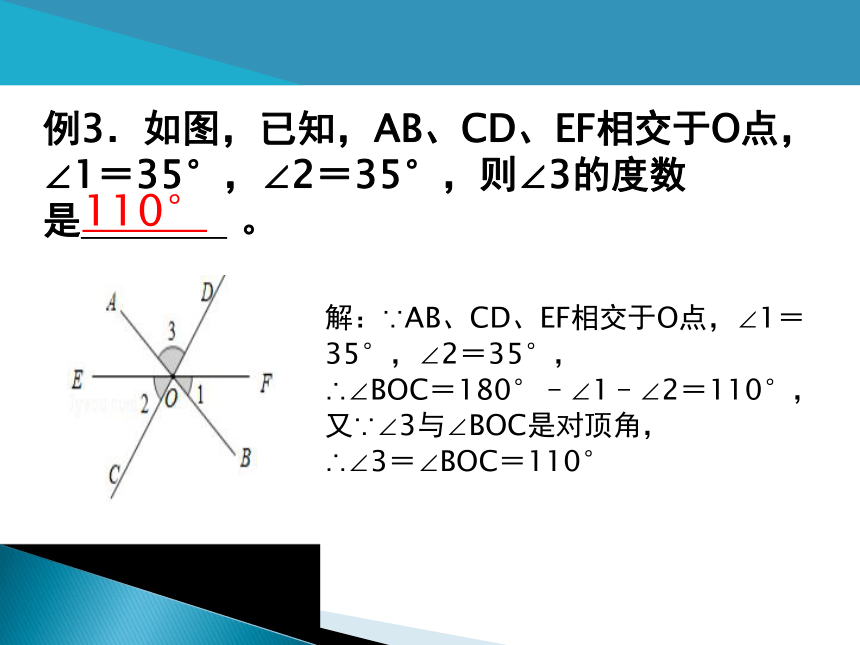
例3.如图,已知,AB、CD、EF相交于O点,∠1=35°,∠2=35°,则∠3的度数是
。
110°
解:∵AB、CD、EF相交于O点,∠1=35°,∠2=35°,
∴∠BOC=180°﹣∠1﹣∠2=110°,
又∵∠3与∠BOC是对顶角,
∴∠3=∠BOC=110°
PART
01
工作概述
PART
04
未来展望
例4.如图是一把剪刀,若∠AOB+∠COD=60°,则∠BOD=
。
150°
解:∵∠AOB=∠COD,且∠AOB+∠COD=60°,
∴∠AOB=30°,
则∠BOD=180°﹣∠AOB=150°
知识点3:垂线
(1)垂线的定义
当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,它们的交点叫做垂足.
(2)垂线的性质
在平面内,过一点有且只有一条直线与已知直线垂直.
注意:“有且只有”中,“有”指“存在”,“只有”指“唯一”
“过一点”的点在直线上或直线外都可以.
PART
01
工作概述
PART
04
未来展望
例5.如图,已知BO⊥AD于点O,∠COE=90°,且∠BOC=4∠AOC,则∠BOE的度数为
度。
18
解:∵BO⊥AD,
∴∠AOB=90°,即∠AOC+∠BOC=90°,
∵∠BOC=4∠AOC,
∴∠AOC+4∠AOC=90°,
∵∠AOC=18°,
∴∠BOC=72°,
∵∠COE=90°,
∴∠BOE=90°﹣∠BOC
=90°﹣72°=18°
PART
01
工作概述
例6.如图,直线AB,CD相交于点O,EO⊥CD,垂足为O.若∠AOE=55°,则∠BOD的度数为
。
145°
解:∵EO⊥CD,
∴∠EOC=90°,
∵∠AOE=55°,
∴∠AOC=145°,
∴∠BOD=145°
PART
01
工作概述
PART
04
未来展望
例7.如图,直线AB、CD相交于点O,OE⊥AB于O,∠DOE=35°,则∠AOC=
。
55°
解:如图,∵OE⊥AB于O,
∴∠BOE=90°.
又∵∠DOE=35°,∠BOD=∠BOE﹣∠DOE,
∴∠BOD=55°,
∴∠AOC=∠BOD=55°
知识点4:垂线段最短
(1)垂线段:从直线外一点引一条直线的垂线,这点和垂足之间的线段叫做垂线段.
(2)垂线段的性质:垂线段最短.
正确理解此性质,垂线段最短,指的是从直线外一点到这条直线所作的垂线段最短.它是相对于这点与直线上其他各点的连线而言.
(3)实际问题中涉及线路最短问题时,其理论依据应从“两点之间,线段最短”和“垂线段最短”这两个中去选择.
PART
01
工作概述
PART
04
未来展望
例8.如图,为了把河中的水引到C处,可过点C作CD⊥AB于D,然后沿CD开渠,这样做可使所开的渠道最短,这种设计的依据
垂线段最短
解:过D点引CD⊥AB于D,然后沿CD开渠,可使所开渠道最短,这种设计的依据是垂线段最短
PART
01
工作概述
PART
04
未来展望
例9.如图,想过点A建一座桥,搭建方式最短的是垂直于河两岸的AO,理由是
垂线段最短。
解:∵AO⊥BD,
∴由垂线段最短可知AO是最短的
知识点5:点到直线的距离
(1)点到直线的距离:直线外一点到直线的垂线段的长度,叫做点到直线的距离.
(2)点到直线的距离是一个长度,而不是一个图形,也就是垂线段的长度,而不是垂线段.它只能量出或求出,而不能说画出,画出的是垂线段这个图形.
PART
01
工作概述
PART
04
未来展望
例10.如图,从点P向直线l所画的4条线段中,线段
最短,理由(
)是(
)
PB
从直线外一点,到直线上各点所连的线段中,垂直线段最短
解:根据“垂线段最短”可知,PB最短,
理由是从直线外一点,到直线上各点所连的线段中,垂直线段最短
PART
01
工作概述
PART
04
未来展望
例11.如图,若直线AB⊥l于点B,BC⊥l于点B,则直线AB和BC重合,这句话蕴含的数学原理是
在平面内,过一点有且只有一条直线与已知直线垂直。
解:因为直线AB⊥l于点B,BC⊥l于点B,
所以直线AB和BC重合(在平面内,过一点有且只有一条直线与已知直线垂直),
故答案为:在平面内,过一点有且只有一条直线与已知直线垂直
知识点6:同位角、内错角、同旁内角
(1)同位角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角.
(2)内错角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的两旁,则这样一对角叫做内错角.
(3)同旁内角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的同旁,则这样一对角叫做同旁内角.
(4)三线八角中的某两个角是不是同位角、内错角或同旁内角,完全由那两个角在图形中的相对位置决定.在复杂的图形中判别三类角时,应从角的两边入手,具有上述关系的角必有两边在同一直线上,此直线即为截线,而另外不在同一直线上的两边,它们所在的直线即为被截的线.同位角的边构成“F“形,内错角的边构成“Z“形,同旁内角的边构成“U”形.
PART
01
工作概述
PART
04
未来展望
例12.如图,有下列判断:
①∠A与∠1是同位角;②∠A与∠B是同旁内角;
③∠4与∠C是内错角;④∠2与∠3是对顶角.
其中正确的是
(填序号)。
①②④
解:①∠A与∠1是同位角,说法正确;
②∠A与∠B是同旁内角,说法正确;
③∠4与∠C是内错角,说法错误,应为同旁内角;
④∠2与∠3是对顶角,说法正确,
正确的说法有①②④
PART
01
工作概述
PART
04
未来展望
例13.如图,图中有
对同位角。
10
解:同位角有:
∠MEB和∠MGD,∠MEA和∠MGC,∠NGD和∠NEB,∠NGC和∠NEA,
∠MEF和∠MGH,∠NEF和∠NGH,∠MEA和∠MGH;∠MEF和∠MGC,
∠NGH和∠NEA,∠MGC和∠MEF.
共有10对
PART
01
工作概述
PART
04
未来展望
例14.如图所示,∠A和∠ACD是直线AB,CD被
所截形成的内错角;∠B的同位角有(
)。
∠ECD,∠ACE
AC
解:如图所示,∠A和∠ACD是直线AB,CD被AC所截形成的内错角;
∠B的同位角是∠ECD,∠ACE
PART
01
工作概述
PART
04
未来展望
例15.如图,∠1与∠2是同位角的是
。
①②
解:这四个图中,∠1与∠2有一条边在同一条直线上,另一条边在被截线的同一方,是同位角,符合的有图①②
PART
01
工作概述
PART
04
未来展望
例16.如图,与∠C是内错角的是
。
∠2,∠3
解:如图所示,与∠C是内错角的是∠2,∠3
完成课后作业
七年级下册数学
第五章相交线与平行线
5.1
相交线
巩固与提高
知识点1:相交线
知识点2:对顶角、邻补角
知识点3:垂线
知识点4:垂线段最短
知识点5:点到直线的距离
知识点6:同位角、内错角、同旁内角
知识点1:相交线
(1)相交线的定义
两条直线交于一点,我们称这两条直线相交.相对的,我们称这两条直线为相交线.
(2)两条相交线在形成的角中有特殊的数量关系和位置关系的有对顶角和邻补角两类.
(3)在同一平面内,两条直线的位置关系有两种:平行和相交(重合除外).
例1.平面内两两相交的6条直线,其交点个数最少为
个,最多为
个,n条直线两两相交的直线最多有
个交点。
1
15
解:根据题意可得:6条直线相交于一点时交点最少,此时交点为1个;
若平面内有相交的2条直线,则最多有1个交点;(即:1=
=1);
若平面内有两两相交的3条直线,则最多有3个交点;(即:1+2=
=3);
若平面内有两两相交的4条直线,则最多有6个交点;(即:1+2+3=
=6);
若平面内有两两相交的5条直线,则最多有10个交点;
(即:1+2+3+4=
=10);
则平面内两两相交的6条直线,其交点个数最多有15个交点;
(即1+2+3+4+5=
=15);
若平面内有n条直线两两相交,则最多有
个交点;
知识点2:对顶角、邻补角
(1)对顶角:有一个公共顶点,并且一个角的两边分别是另一个角的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.
(2)邻补角:只有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角.
(3)对顶角的性质:对顶角相等.
(4)邻补角的性质:邻补角互补,即和为180°.
(5)邻补角、对顶角成对出现,在相交直线中,一个角的邻补角有两个.邻补角、对顶角都是相对与两个角而言,是指的两个角的一种位置关系.它们都是在两直线相交的前提下形成的.
PART
01
工作概述
PART
04
未来展望
例2.如图,两条直线AB,CD交于点O,射线OM是∠AOC的平分线,若∠BOD=80°,
则∠BOM的度数是
。
解:∵∠BOD=80°,
∴∠AOC=80°,∠COB=100°,
∵射线OM是∠AOC的平分线,
∴∠COM=40°,
∴∠BOM=40°+100°=140°
140°
PART
01
工作概述
PART
04
未来展望
例3.如图,已知,AB、CD、EF相交于O点,∠1=35°,∠2=35°,则∠3的度数是
。
110°
解:∵AB、CD、EF相交于O点,∠1=35°,∠2=35°,
∴∠BOC=180°﹣∠1﹣∠2=110°,
又∵∠3与∠BOC是对顶角,
∴∠3=∠BOC=110°
PART
01
工作概述
PART
04
未来展望
例4.如图是一把剪刀,若∠AOB+∠COD=60°,则∠BOD=
。
150°
解:∵∠AOB=∠COD,且∠AOB+∠COD=60°,
∴∠AOB=30°,
则∠BOD=180°﹣∠AOB=150°
知识点3:垂线
(1)垂线的定义
当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,它们的交点叫做垂足.
(2)垂线的性质
在平面内,过一点有且只有一条直线与已知直线垂直.
注意:“有且只有”中,“有”指“存在”,“只有”指“唯一”
“过一点”的点在直线上或直线外都可以.
PART
01
工作概述
PART
04
未来展望
例5.如图,已知BO⊥AD于点O,∠COE=90°,且∠BOC=4∠AOC,则∠BOE的度数为
度。
18
解:∵BO⊥AD,
∴∠AOB=90°,即∠AOC+∠BOC=90°,
∵∠BOC=4∠AOC,
∴∠AOC+4∠AOC=90°,
∵∠AOC=18°,
∴∠BOC=72°,
∵∠COE=90°,
∴∠BOE=90°﹣∠BOC
=90°﹣72°=18°
PART
01
工作概述
例6.如图,直线AB,CD相交于点O,EO⊥CD,垂足为O.若∠AOE=55°,则∠BOD的度数为
。
145°
解:∵EO⊥CD,
∴∠EOC=90°,
∵∠AOE=55°,
∴∠AOC=145°,
∴∠BOD=145°
PART
01
工作概述
PART
04
未来展望
例7.如图,直线AB、CD相交于点O,OE⊥AB于O,∠DOE=35°,则∠AOC=
。
55°
解:如图,∵OE⊥AB于O,
∴∠BOE=90°.
又∵∠DOE=35°,∠BOD=∠BOE﹣∠DOE,
∴∠BOD=55°,
∴∠AOC=∠BOD=55°
知识点4:垂线段最短
(1)垂线段:从直线外一点引一条直线的垂线,这点和垂足之间的线段叫做垂线段.
(2)垂线段的性质:垂线段最短.
正确理解此性质,垂线段最短,指的是从直线外一点到这条直线所作的垂线段最短.它是相对于这点与直线上其他各点的连线而言.
(3)实际问题中涉及线路最短问题时,其理论依据应从“两点之间,线段最短”和“垂线段最短”这两个中去选择.
PART
01
工作概述
PART
04
未来展望
例8.如图,为了把河中的水引到C处,可过点C作CD⊥AB于D,然后沿CD开渠,这样做可使所开的渠道最短,这种设计的依据
垂线段最短
解:过D点引CD⊥AB于D,然后沿CD开渠,可使所开渠道最短,这种设计的依据是垂线段最短
PART
01
工作概述
PART
04
未来展望
例9.如图,想过点A建一座桥,搭建方式最短的是垂直于河两岸的AO,理由是
垂线段最短。
解:∵AO⊥BD,
∴由垂线段最短可知AO是最短的
知识点5:点到直线的距离
(1)点到直线的距离:直线外一点到直线的垂线段的长度,叫做点到直线的距离.
(2)点到直线的距离是一个长度,而不是一个图形,也就是垂线段的长度,而不是垂线段.它只能量出或求出,而不能说画出,画出的是垂线段这个图形.
PART
01
工作概述
PART
04
未来展望
例10.如图,从点P向直线l所画的4条线段中,线段
最短,理由(
)是(
)
PB
从直线外一点,到直线上各点所连的线段中,垂直线段最短
解:根据“垂线段最短”可知,PB最短,
理由是从直线外一点,到直线上各点所连的线段中,垂直线段最短
PART
01
工作概述
PART
04
未来展望
例11.如图,若直线AB⊥l于点B,BC⊥l于点B,则直线AB和BC重合,这句话蕴含的数学原理是
在平面内,过一点有且只有一条直线与已知直线垂直。
解:因为直线AB⊥l于点B,BC⊥l于点B,
所以直线AB和BC重合(在平面内,过一点有且只有一条直线与已知直线垂直),
故答案为:在平面内,过一点有且只有一条直线与已知直线垂直
知识点6:同位角、内错角、同旁内角
(1)同位角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角.
(2)内错角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的两旁,则这样一对角叫做内错角.
(3)同旁内角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的同旁,则这样一对角叫做同旁内角.
(4)三线八角中的某两个角是不是同位角、内错角或同旁内角,完全由那两个角在图形中的相对位置决定.在复杂的图形中判别三类角时,应从角的两边入手,具有上述关系的角必有两边在同一直线上,此直线即为截线,而另外不在同一直线上的两边,它们所在的直线即为被截的线.同位角的边构成“F“形,内错角的边构成“Z“形,同旁内角的边构成“U”形.
PART
01
工作概述
PART
04
未来展望
例12.如图,有下列判断:
①∠A与∠1是同位角;②∠A与∠B是同旁内角;
③∠4与∠C是内错角;④∠2与∠3是对顶角.
其中正确的是
(填序号)。
①②④
解:①∠A与∠1是同位角,说法正确;
②∠A与∠B是同旁内角,说法正确;
③∠4与∠C是内错角,说法错误,应为同旁内角;
④∠2与∠3是对顶角,说法正确,
正确的说法有①②④
PART
01
工作概述
PART
04
未来展望
例13.如图,图中有
对同位角。
10
解:同位角有:
∠MEB和∠MGD,∠MEA和∠MGC,∠NGD和∠NEB,∠NGC和∠NEA,
∠MEF和∠MGH,∠NEF和∠NGH,∠MEA和∠MGH;∠MEF和∠MGC,
∠NGH和∠NEA,∠MGC和∠MEF.
共有10对
PART
01
工作概述
PART
04
未来展望
例14.如图所示,∠A和∠ACD是直线AB,CD被
所截形成的内错角;∠B的同位角有(
)。
∠ECD,∠ACE
AC
解:如图所示,∠A和∠ACD是直线AB,CD被AC所截形成的内错角;
∠B的同位角是∠ECD,∠ACE
PART
01
工作概述
PART
04
未来展望
例15.如图,∠1与∠2是同位角的是
。
①②
解:这四个图中,∠1与∠2有一条边在同一条直线上,另一条边在被截线的同一方,是同位角,符合的有图①②
PART
01
工作概述
PART
04
未来展望
例16.如图,与∠C是内错角的是
。
∠2,∠3
解:如图所示,与∠C是内错角的是∠2,∠3
完成课后作业
