华东师大版八年级数学下册课件:20.3数据的离散程度(共24张PPT)
文档属性
| 名称 | 华东师大版八年级数学下册课件:20.3数据的离散程度(共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-17 15:27:31 | ||
图片预览




文档简介
(共24张PPT)
第20章
数据的整理与初步处理
20.3
数据的离散程度
八年级下册
我们常用平均数、中位数来刻画数据的“平均水平”,但在有些情况下“平均水平”是不够的,如评价选手的射击水平、机器加工零件的精度、手表的日走时误差时,还需要用一个新的数来刻画一组数据的波动情况.
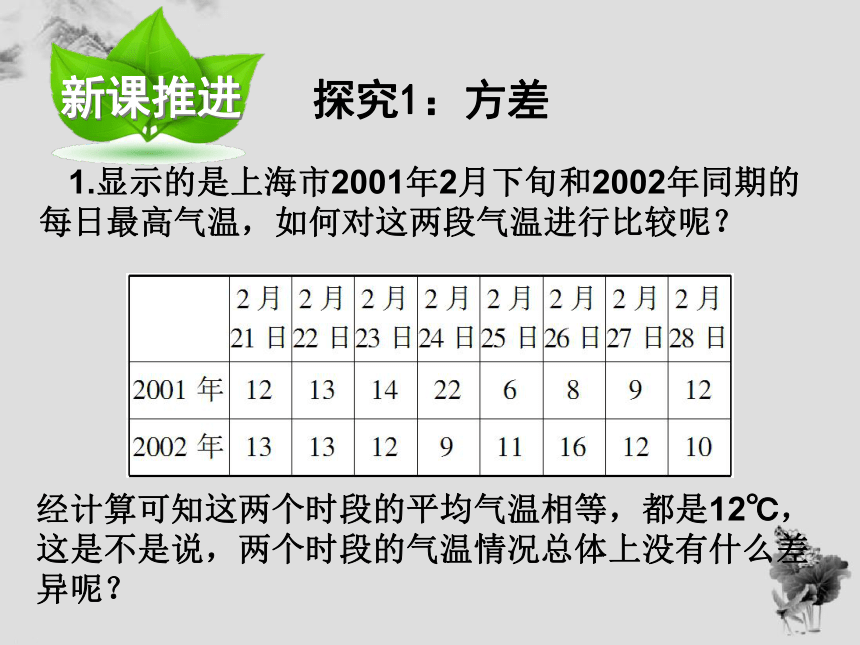
1.显示的是上海市2001年2月下旬和2002年同期的每日最高气温,如何对这两段气温进行比较呢?
经计算可知这两个时段的平均气温相等,都是12℃,这是不是说,两个时段的气温情况总体上没有什么差异呢?
探究1:方差
探究
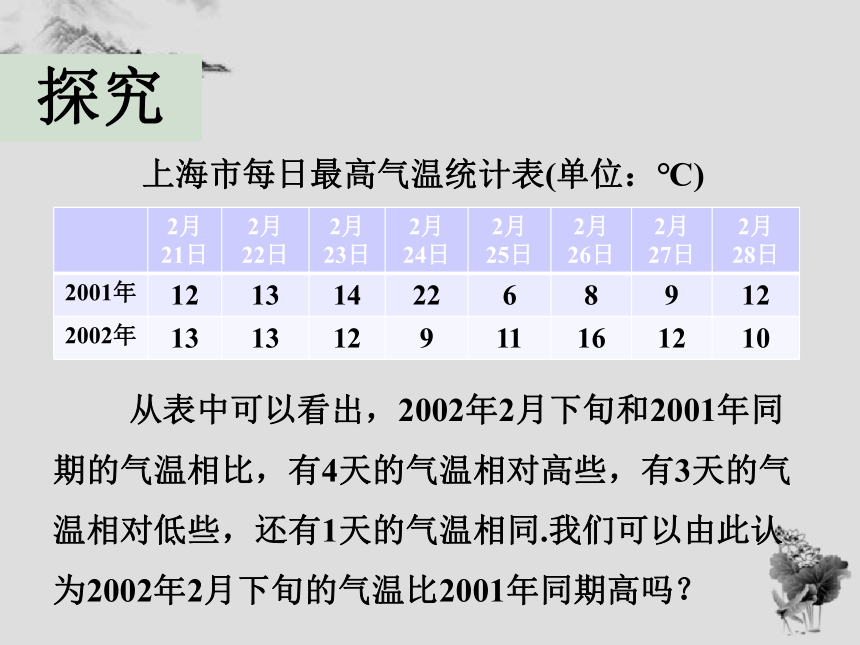
从表中可以看出,2002年2月下旬和2001年同期的气温相比,有4天的气温相对高些,有3天的气温相对低些,还有1天的气温相同.我们可以由此认为2002年2月下旬的气温比2001年同期高吗?
上海市每日最高气温统计表(单位:℃)
2月21日
2月
22日
2月
23日
2月
24日
2月
25日
2月
26日
2月
27日
2月
28日
2001年
12
13
14
22
6
8
9
12
2002年
13
13
12
9
11
16
12
10
探究
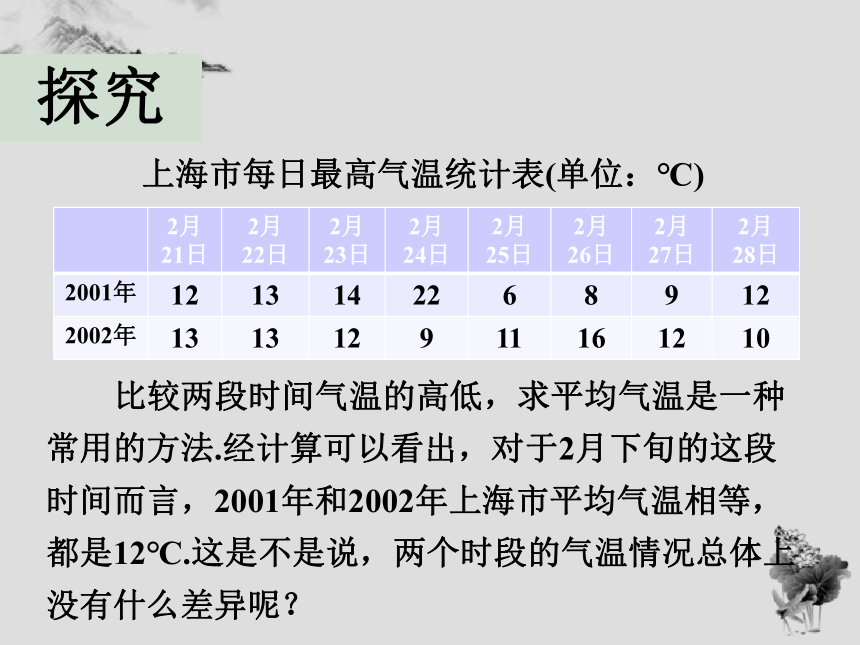
比较两段时间气温的高低,求平均气温是一种常用的方法.经计算可以看出,对于2月下旬的这段时间而言,2001年和2002年上海市平均气温相等,都是12℃.这是不是说,两个时段的气温情况总体上没有什么差异呢?
上海市每日最高气温统计表(单位:℃)
2月21日
2月
22日
2月
23日
2月
24日
2月
25日
2月
26日
2月
27日
2月
28日
2001年
12
13
14
22
6
8
9
12
2002年
13
13
12
9
11
16
12
10
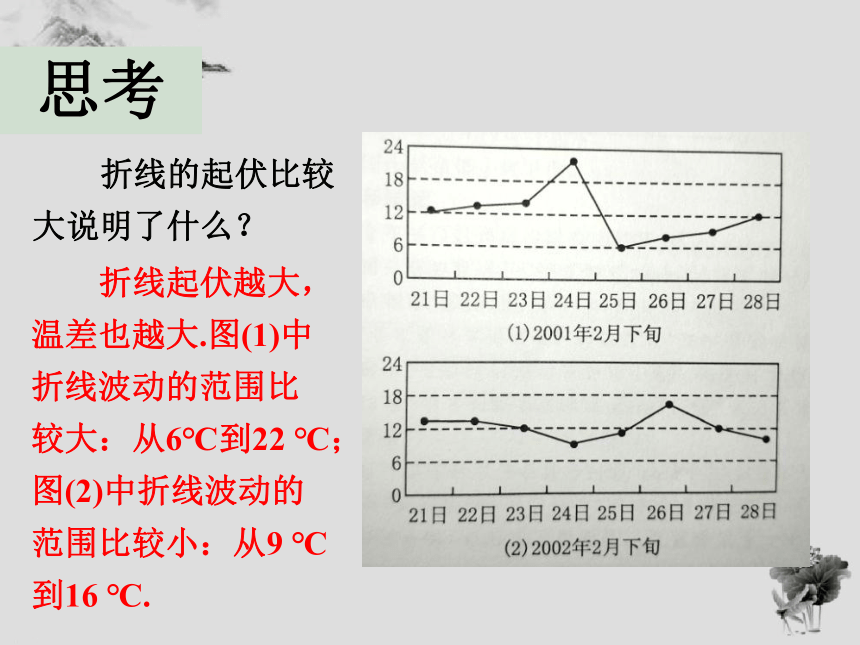
思考
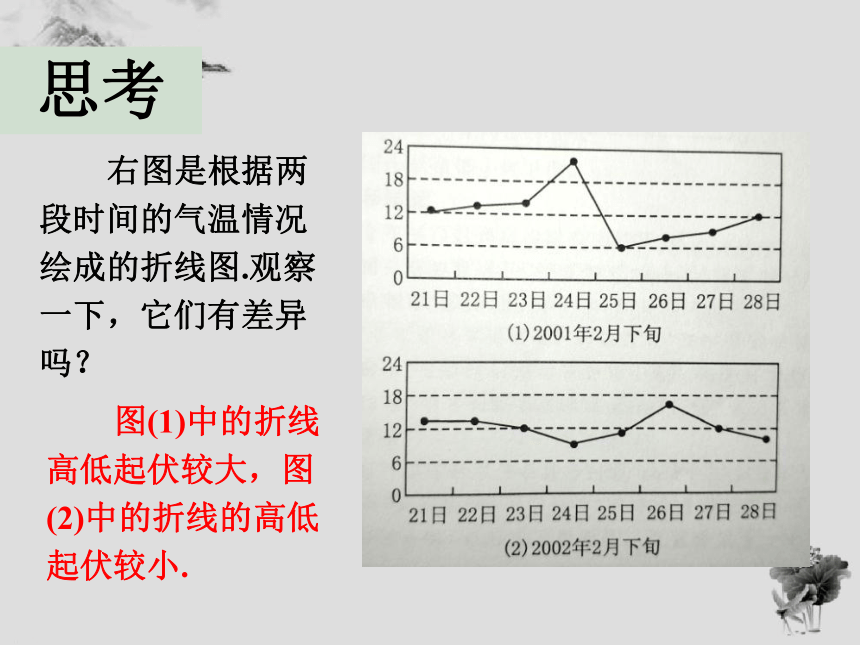
右图是根据两段时间的气温情况绘成的折线图.观察一下,它们有差异吗?
图(1)中的折线高低起伏较大,图(2)中的折线的高低起伏较小.
思考
折线的起伏比较大说明了什么?
折线起伏越大,温差也越大.图(1)中折线波动的范围比较大:从6℃到22
℃;图(2)中折线波动的范围比较小:从9
℃到16
℃.
思考
这种气温的不同在平均数中能体现出来吗?用什么样的数来反映这种特征比较合适?
气温的最大值、气温的最小值可以用来表示数据高低起伏的变化大小.
思考
我们说两个城市,一个“四季温差不大”,一个“四季分明”.用数学术语应该怎样表示?
问题2
小明和小兵两人参加体育项目训练,近期的5次测试成绩如下表所示.请问谁的成绩较为稳定?为什么?
测试次数
1
2
3
4
5
小明
10
14
13
12
13
小兵
11
11
15
14
11
分析
通过计算,我们发现两人测试成绩的平均数都是12.4,把他们的成绩画图如下.
分析
从图中我们可以看到:相比之下,小明的成绩大部分集中在12.4附近,而小兵的成绩与其平均数的离散程度略大.
通常,如果一组数据与其平均数的离散程度较小,我们就说它比较稳定.
归纳
我们可以用“先平均,再求差,然后平方,最后再平均”得到的结果表示一组数据偏离平均值的情况,这个结果通常称为方差.
问题2
测试次数
1
2
3
4
5
小明
10
14
13
12
13
小兵
11
11
15
14
11
(3)
,输入所有数据;
探究2:用计算器求方差
用笔算的方法计算方差比较繁琐,如果能够用计算器,就会大大提高效率,下面以计算2002年2月下旬的上海市每日最高气温的方差为例,按键的顺序如下:
(1)
,打开计算器;
(2)
,启动统计计算功能;
(4)
,得到一个数值;最后,将该数值平方,即是我们要计算的方差.
1.正确的是(
)
A.两组数据,平均数越大,波动越大
B.两组数据,中位数越大,波动越大
C.两组数据,方差越大,波动越大
D.两组数据的波动大小由平均数、方差共同说明
C
练习
比较下列两组数据的方差:
A组:0,10,5,5,5,5,5,5,5,5;
B组:4,6,3,7,2,8,1,9,5,5.
平均数都是5,带入方差公式:
计算得:A组方差5,B组方差6.
练习
计算问题1中哪一年2月下旬每日最高气温的离散程度较大?与图中直观看出来的结果一致吗?
经计算可知这两个时段的平均气温都是12
℃.
代入方差公式可得2001年和2002年2月下旬每日最高气温的方差分别为20.75和4.
可以看出2001年离散程度较大;与图中直观得出的结论一致.
2月21日
2月
22日
2月
23日
2月
24日
2月
25日
2月
26日
2月
27日
2月
28日
2001年
12
13
14
22
6
8
9
12
2002年
13
13
12
9
11
16
12
10
练习
下表给出了两种股票从2002年4月1日到4月19日的交易日收盘价格,分别计算它们的平均数和方差,并比较这两种股票在这段时间内的涨跌变化幅度.
经计算可知A股票的平均数约为11.72,B股票平均数约为14.16,代入方差公式可得A股票方差约为0.10;B股票方差约为0.18.所以B股票价格整体波动比A股票大一些.
2.甲、乙、丙三台包装机同时分装质量为400克的茶叶,从它们各自分装的茶叶中分别随机抽取了10盒,测得它们的实际质量的方差如下表所示:
根据表中数据,可以认为三台包装机中,
____包装机包装的茶叶质量最稳定.
乙
解:乙包装机包装的茶叶质量最稳定.
3.某校要从甲、乙两名跳远运动员中挑选一人参加一项校际比赛,抽查了两人在最近10次选拔赛中的成绩(单位:cm)如下:
甲:585
596
610
598
612
597
604
600
613
601
乙:613
618
580
574
618
593
585
590
598
624
你认为该派谁参加?
解析:此题可从平均数,方差两方面去分析.当平均数相差不大时,再看方差.
这节课你有哪些收获?
方差反映了一组数据的波动情况,方差公式是:
1.从教材习题中选取,
2.完成练习册本课时的习题.
第20章
数据的整理与初步处理
20.3
数据的离散程度
八年级下册
我们常用平均数、中位数来刻画数据的“平均水平”,但在有些情况下“平均水平”是不够的,如评价选手的射击水平、机器加工零件的精度、手表的日走时误差时,还需要用一个新的数来刻画一组数据的波动情况.
1.显示的是上海市2001年2月下旬和2002年同期的每日最高气温,如何对这两段气温进行比较呢?
经计算可知这两个时段的平均气温相等,都是12℃,这是不是说,两个时段的气温情况总体上没有什么差异呢?
探究1:方差
探究
从表中可以看出,2002年2月下旬和2001年同期的气温相比,有4天的气温相对高些,有3天的气温相对低些,还有1天的气温相同.我们可以由此认为2002年2月下旬的气温比2001年同期高吗?
上海市每日最高气温统计表(单位:℃)
2月21日
2月
22日
2月
23日
2月
24日
2月
25日
2月
26日
2月
27日
2月
28日
2001年
12
13
14
22
6
8
9
12
2002年
13
13
12
9
11
16
12
10
探究
比较两段时间气温的高低,求平均气温是一种常用的方法.经计算可以看出,对于2月下旬的这段时间而言,2001年和2002年上海市平均气温相等,都是12℃.这是不是说,两个时段的气温情况总体上没有什么差异呢?
上海市每日最高气温统计表(单位:℃)
2月21日
2月
22日
2月
23日
2月
24日
2月
25日
2月
26日
2月
27日
2月
28日
2001年
12
13
14
22
6
8
9
12
2002年
13
13
12
9
11
16
12
10
思考
右图是根据两段时间的气温情况绘成的折线图.观察一下,它们有差异吗?
图(1)中的折线高低起伏较大,图(2)中的折线的高低起伏较小.
思考
折线的起伏比较大说明了什么?
折线起伏越大,温差也越大.图(1)中折线波动的范围比较大:从6℃到22
℃;图(2)中折线波动的范围比较小:从9
℃到16
℃.
思考
这种气温的不同在平均数中能体现出来吗?用什么样的数来反映这种特征比较合适?
气温的最大值、气温的最小值可以用来表示数据高低起伏的变化大小.
思考
我们说两个城市,一个“四季温差不大”,一个“四季分明”.用数学术语应该怎样表示?
问题2
小明和小兵两人参加体育项目训练,近期的5次测试成绩如下表所示.请问谁的成绩较为稳定?为什么?
测试次数
1
2
3
4
5
小明
10
14
13
12
13
小兵
11
11
15
14
11
分析
通过计算,我们发现两人测试成绩的平均数都是12.4,把他们的成绩画图如下.
分析
从图中我们可以看到:相比之下,小明的成绩大部分集中在12.4附近,而小兵的成绩与其平均数的离散程度略大.
通常,如果一组数据与其平均数的离散程度较小,我们就说它比较稳定.
归纳
我们可以用“先平均,再求差,然后平方,最后再平均”得到的结果表示一组数据偏离平均值的情况,这个结果通常称为方差.
问题2
测试次数
1
2
3
4
5
小明
10
14
13
12
13
小兵
11
11
15
14
11
(3)
,输入所有数据;
探究2:用计算器求方差
用笔算的方法计算方差比较繁琐,如果能够用计算器,就会大大提高效率,下面以计算2002年2月下旬的上海市每日最高气温的方差为例,按键的顺序如下:
(1)
,打开计算器;
(2)
,启动统计计算功能;
(4)
,得到一个数值;最后,将该数值平方,即是我们要计算的方差.
1.正确的是(
)
A.两组数据,平均数越大,波动越大
B.两组数据,中位数越大,波动越大
C.两组数据,方差越大,波动越大
D.两组数据的波动大小由平均数、方差共同说明
C
练习
比较下列两组数据的方差:
A组:0,10,5,5,5,5,5,5,5,5;
B组:4,6,3,7,2,8,1,9,5,5.
平均数都是5,带入方差公式:
计算得:A组方差5,B组方差6.
练习
计算问题1中哪一年2月下旬每日最高气温的离散程度较大?与图中直观看出来的结果一致吗?
经计算可知这两个时段的平均气温都是12
℃.
代入方差公式可得2001年和2002年2月下旬每日最高气温的方差分别为20.75和4.
可以看出2001年离散程度较大;与图中直观得出的结论一致.
2月21日
2月
22日
2月
23日
2月
24日
2月
25日
2月
26日
2月
27日
2月
28日
2001年
12
13
14
22
6
8
9
12
2002年
13
13
12
9
11
16
12
10
练习
下表给出了两种股票从2002年4月1日到4月19日的交易日收盘价格,分别计算它们的平均数和方差,并比较这两种股票在这段时间内的涨跌变化幅度.
经计算可知A股票的平均数约为11.72,B股票平均数约为14.16,代入方差公式可得A股票方差约为0.10;B股票方差约为0.18.所以B股票价格整体波动比A股票大一些.
2.甲、乙、丙三台包装机同时分装质量为400克的茶叶,从它们各自分装的茶叶中分别随机抽取了10盒,测得它们的实际质量的方差如下表所示:
根据表中数据,可以认为三台包装机中,
____包装机包装的茶叶质量最稳定.
乙
解:乙包装机包装的茶叶质量最稳定.
3.某校要从甲、乙两名跳远运动员中挑选一人参加一项校际比赛,抽查了两人在最近10次选拔赛中的成绩(单位:cm)如下:
甲:585
596
610
598
612
597
604
600
613
601
乙:613
618
580
574
618
593
585
590
598
624
你认为该派谁参加?
解析:此题可从平均数,方差两方面去分析.当平均数相差不大时,再看方差.
这节课你有哪些收获?
方差反映了一组数据的波动情况,方差公式是:
1.从教材习题中选取,
2.完成练习册本课时的习题.
