2020年春苏科版数学七年级下册9.5 多项式的因式分解 提优练习(2小节)含答案
文档属性
| 名称 | 2020年春苏科版数学七年级下册9.5 多项式的因式分解 提优练习(2小节)含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 58.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-17 15:05:40 | ||
图片预览




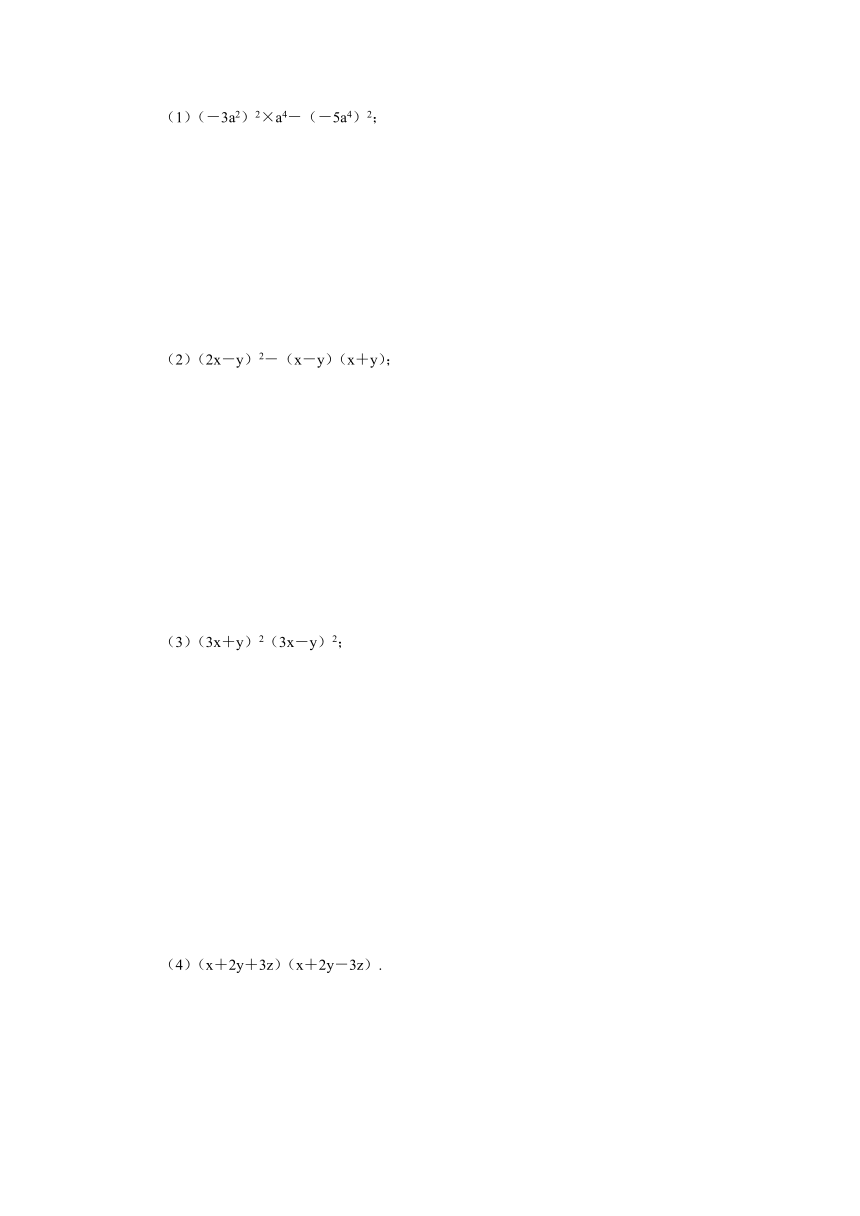
文档简介
多项式的因式分解
因式分解的综合应用
1.
多项式4x2-4与多项式x2-2x+1的公因式是( )
A.
x+1
B.
x-1
C.
x2-1
D.
(x-1)2
2.
(2018·百色)因式分解x-4x3的最后结果是( )
A.
x(1-2x)2
B.
x(2x-1)(2x+1)
C.
x(1-2x)(2x+1)
D.
x(1-4x2)
3.
(2019春·重庆沙坪坝区校级月考)下列因式分解不正确的是( )
A.
3a2b-6ab+3b=3b(a-1)2
B.
-4b2+36a2=4(3a+b)(3a-b)
C.
x2(a-b)-4(b-a)=(a-b)(x+2)(x-2)
D.
(a2+1)2-4a2=(a+1)2(a-1)2
4.
分解因式:
(1)(2019·扬州)a3b-9ab= W.
(2)(2019·广安)3a4-3b4= W.
(3)9x2-(x+2y)2= W.
5.
(1)若mn=3,a+b=4,a-b=5,则mna2-nmb2的值是 W.
(2)(2019·长春一模)若ab=-2,a-3b=5,则a3b-6a2b2+9ab3的值为 W.
6.
(2019春·南京玄武区校级期中)因式分解:
将下列各式因式分解:
(1)16(m+n)2-9(m-n)2;
(2)-8a(a+1)2+2a3;
(3)(x2-2x-2)(x2-2x+4)+9.
12.
若a,b,c是△ABC的三边,试判断代数式(a2+b2-c2)2-4a2b2的值是正数还是负数.
提优测试卷,(时间:90分钟 满分:100分))
一、
选择题(每小题3分,共24分)
1.
若□×3xy=3x2y,则□内应填的单项式是( )
A.
xy
B.
3xy
C.
x
D.
3x
2.
下列各运算中,正确的是( )
A.
(m-2)2=m2-4
B.
(1+2a)2=1+2a+4a2
C.
(a+1)(-a-1)=a2-1
D.
(a+1)(-1+a)=a2-1
3.
已知(x+y)2=7,(x-y)2=5,则xy的值是( )
A.
1
B.
-1
C.
D.
-
4.
(2019春·泰兴期中)若(x2+px+2)(x-3)的乘积中不含x2项,则p的值为( )
A.
3
B.
-3
C.
±3
D.
无法确定
5.
(2019春·盐城大丰区期末)多项式ax2-a与多项式ax2-2ax+a的公因式是( )
A.
a
B.
x-1
C.
a(x-1)
D.
a(x2-1)
6.
(2019春·深圳龙岗区期末)已知a+b=-5,ab=-4,则a2-3ab+b2的值是( )
A.
49
B.
37
C.
45
D.
33
7.
如果257+513能被n整除,则n的值可能是( )
A.
20
B.
30
C.
35
D.
40
8.
(2019春·苏州高新区校级期中)现有一张边长为a的大正方形卡片和三张边长为b的小正方形卡片
(如图①),取出两张小正方形卡片放入“大正方形卡片”内拼成的图案如图②,再重新用两张小正方形卡片放入“大正方形卡片”内拼成的图案如图③.已知图③中阴影部分的面积比图②中阴影部分的面积大2ab-6,则小正方形卡片的面积是( )
A.
2
B.
3
C.
4
D.
5
二、
填空题(每小题3分,共30分)
9.
计算:(1)(2a)3(-3ab2)= ;
(2)x(2x2-3x+1)= ;
(3)(3a+b)(-3a-b)= W.
10.
因式分解:
(1)(2019·沈阳)-x2-4y2+4xy= W.
(2)(2019·宁夏)2a3-8a= W.
11.
(2019春·深圳福田区期末)若mn=1,m-n=2,则m2n-mn2的值是 W.
12.
(2019春·无锡锡山区校级月考)已知三项式9x2+1+是一个完全平方式,但是其中一项看不清了,你认为这一项应该是 (写出一个你认为正确的答案即可).
13.
计算:2342-468×134+1342= W.
14.
已知n为整数,若(2n+1)2-(2n-1)2的值总能被整数m整除,则m的最大值为 W.
15.
(2019春·东台期中)我们规定一种运算:=ad-bc,例如=3×6-4×5=-2.按照这种运算规定,已知=0,则x= W.
16.
从一个边长为2a+b的大正方形中剪出一个边长为b的小正方形,剩余的部分正好能剪拼成四个宽为a的长方形,那么每个长方形的长为 W.
17.
已知a2-2a+b2+4b+5=0,则ab= W.
18.
已知m+=3,则m4+= W.
三、
解答题(共46分)
19.
(8分)(2019春·扬州江都区期中)计算:
(1)(-3a2)2×a4-(-5a4)2;
(2)(2x-y)2-(x-y)(x+y);
(3)(3x+y)2(3x-y)2;
(4)(x+2y+3z)(x+2y-3z).
20.
(8分)因式分解:
(1)3x3-12x2y+12xy2;
(2)a2(x-y)-4x+4y;
(3)(x2+4y2)2-16x2y2;
(4)(x-1)2+2(1-x)·y+y2.
21.
(8分)化简求值:
(1)(a-2b)2+(a-b)(a+b)-2(a-3b)(a-b),其中a=1,b=-2;
(2)已知m+n=3,mn=,求m2+(n-mn)2+2mn-2m2n的值.
23.
(8分)如图,边长为a的正方形ABCD和边长为b(a>b)的正方形CEFG拼在一起,B,C,E三点在同一直线上,设图中阴影部分的面积为S.
(1)如图①,S的值与a的大小有关吗?说明理由.
(2)如图②,若a-b=2,a2+b2=7,求S2的值.
24.
(8分)(枣庄中考题)我们知道,任意一个正整数n都可以进行这样的分解:n=p×q(p,q是正整数,且p≤q),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p×q是n的最佳分解.并规定:F(n)=.
例如12可以分解成1×12,2×6或3×4,因为12-1>6-2>4-3,所以3×4是12的最佳分解,所以F(12)=.
(1)如果一个正整数m是另外一个正整数n的平方,我们称正整数m是完全平方数.试说明对任意一个完全平方数m,总有F(m)=1;
(2)如果一个两位正整数t,t=10x+y(1≤x≤y≤9,x,y为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为36,那么我们称这个数t为“吉祥数”,求所有的“吉祥数”;
(3)在(2)所得“吉祥数”中,求F(t)的最大值.
答案
1.
B 2.
C 3.
C
4.
(1)ab(a+3)(a-3) (2)3(a2+b2)(a+b)(a-b)
(3)4(2x+y)(x-y) 解析:原式=(3x+x+2y)[3x-(x+2y)]=(4x+2y)(2x-2y)=4(2x+y)(x-y).
5.
(1)60 (2)-50
6.
(1)原式=-y(9x2-6xy+y2)=-y(3x-y)2.
(2)原式=m3(a-2)-m(a-2)=m(a-2)(m+1)(m-1).
(3)原式=(9x2-y2)2=(3x+y)2(3x-y)2.
(4)原式=a(x-1)2(x+1)2.
(5)原式=(x2-4x+4)2=(x-2)4.
7.
根据题意,得2a+2b=14,ab=10,
所以a3b+ab3+2a2b2=ab(a2+b2+2ab)=ab(a+b)2=490.
8.
C 解析:原式=2(x+y)(x-y)(a-b),
则呈现的密码信息可能是我爱香港,故选C.
9.
D 解析:由x2-2x-1=0,得到x2=2x+1,x2-2x=1,则原式=2x·x2-7x2+4x-2
019=2x(2x+1)-7(2x+1)+4x-2
019=4x2-8x-7-2
019=4(x2-2x)-2
026=4-2
026=-2
022.故选D.
10.
63,65 解析:248-1=(224+1)(224-1)=(224+1)(212+1)(212-1)=(224+1)(212+1)(26+1)(26-1).因为26=64,所以26-1=63,26+1=65,所以这两个数是63,65.
11.
(1)原式=(4m+4n)2-(3m-3n)2=(4m+4n+3m-3n)(4m+4n-3m+3n)=(7m+n)(m+7n).
(2)原式=2a[a2-4(a+1)2]=2a[a2-(2a+2)2]=2a(a+2a+2)·(a-2a-2)=2a(3a+2)(-a-2)=-2a(3a+2)(a+2).
(3)令x2-2x=t,则
原式=(t-2)(t+4)+9=t2+2t-8+9=t2+2t+1=(t+1)2,
即原式=(x2-2x+1)2=(x-1)4.
12.
原式=(a2+b2-c2+2ab)(a2+b2-c2-2ab)
=[(a+b)2-c2][(a-b)2-c2]
=(a+b+c)(a+b-c)(a-b-c)(a-b+c),
因为a,b,c是△ABC的三边,
所以a+b+c>0,a+b-c>0,a-b-c<0,a-b+c>0,
所以(a+b+c)(a+b-c)(a-b-c)(a-b+c)<0,即原式的值为负数.
13.
【发现】(1)625
(2)a+b=50
【类比】900 说明如下:由题意,得m+n=60,将n=60-m代入mn,
得mn=-m2+60m=-(m-30)2+900,所以当m=30时,mn的最大值为900.
14.
(1)1或- x-1,6x+5 (x-1)(6x+5) 解析:当x=1时,6x2-x-5=0,设6x2-x-5=(x-1)(mx+n),解得m=6,n=5,所以因式分解6x2-x-5=(x-1)(6x+5).
(2)①当x=-1时,2x2+5x+3=0,
所以2x2+5x+3=(x+1)(2x+3).
②当x=1时,x3-7x+6=0,
所以x3-7x+6=(x-1)(x-2)(x+3).
(3)设x3-x2+ax+b=(x2+2x+1)(x+m),
则x3-x2+ax+b=x3+(m+2)x2+(2m+1)x+m,
所以m+2=-1,2m+1=a,m=b,解得a=-5,b=-3,m=-3.
所以x3-x2-5x-3=(x2+2x+1)(x-3)=(x+1)2(x-3).
提优测试卷
1.
C 2.
D 3.
C 4.
A 5.
C 6.
C
7.
B 解析:257+513=514+513=513×(5+1)=513×6=512×30,则n的值可能是30.故选B.
8.
A 解析:题图③中阴影部分的面积为(a-b)2,题图②中阴影部分的面积为(2b-a)2,由题意,得(a-b)2-(2b-a)2=2ab-6,整理,得b2=2,则小正方形卡片的面积是2,故选A.
9.
(1)-24a4b2 (2)2x3-3x2+x (3)-9a2-6ab-b2
10.
(1)-(x-2y)2 (2)2a(a+2)(a-2)
11.
2 12.
6x(答案不唯一) 13.
10
000
14.
8 解析:因为(2n+1)2-(2n-1)2
=(2n+1+2n-1)(2n+1-2n+1)
=4n×2=8n,
所以m的最大值为8.
15.
-
16.
a+b 解析:由题意,得(2a+b)2-b2=(2a+b+b)(2a+b-b)=4a(a+b).故每个长方形的长为a+b.
17.
1 解析:a2-2a+b2+4b+5=a2-2a+1+b2+4b+4=(a-1)2+(b+2)2=0,
所以a-1=0,b+2=0,解得a=1,b=-2,
所以ab=1.
18.
47 解析:m2+=-2·m·=32-2=7,
m4+=-2·m2·=72-2=47.
19.
(1)原式=9a4×a4-25a8=-16a8.
(2)原式=4x2-4xy+y2-x2+y2=3x2-4xy+2y2.
(3)原式=[(3x+y)(3x-y)]2=(9x2-y2)2=81x4-18x2y2+y4.
(4)原式=[(x+2y)+3z][(x+2y)-3z]=(x+2y)2-9z2=x2+4xy+4y2-9z2.
20.
(1)3x(x-2y)2.
(2)(x-y)(a+2)(a-2).
(3)(x+2y)2(x-2y)2.
(4)(x-y-1)2.
21.
(1)原式=a2-4ab+4b2+a2-b2-2(a2-ab-3ab+3b2)=a2-4ab+4b2+a2-b2-2a2+2ab+6ab-6b2=4ab-3b2,
当a=1,b=-2时,原式=4×1×(-2)-3×(-2)2=-8-12=-20.
(2)原式=m2+n2-2mn2+m2n2+2mn-2m2n=(m+n)2+mn(mn-2n-2m)=(m+n)2+mn[mn-2(m+n)],
当m+n=3,mn=时,原式=9+×=.
22.
设67
897=a,则67
898=a+1,67
896=a-1,67
899=a+2,
则67
897×67
898-67
896×67
899
=a(a+1)-(a-1)(a+2)
=(a2+a)-(a2+a-2)
=a2+a-a2-a+2=2.
23.
(1)S的值与a的大小无关,理由如下:
由题意知,S=a2+b2-(a+b)·a-(a-b)·a-b2=b2,
所以S的值与a的大小无关.
(2)因为S=(a-b)·a+(a-b)·b=(a-b)(a+b),
所以S2=(a-b)2(a+b)2.
因为a-b=2,所以(a-b)2=a2-2ab+b2=4.因为a2+b2=7,所以2ab=3,所以(a+b)2=a2+2ab+b2=10,
所以S2=×4×10=10.
24.
(1)对任意一个完全平方数m,设m=n2(n为正整数),
因为|n-n|=0,所以n×n是m的最佳分解,
所以对任意一个完全平方数m,总有F(m)==1.
(2)设交换t的个位上的数与十位上的数得到的新数为t′,
则t′=10y+x.
因为t是“吉祥数”,
所以t′-t=(10y+x)-(10x+y)=9(y-x)=36,
所以y=x+4.
因为1≤x≤y≤9,x,y为自然数,
所以“吉祥数”有15,26,37,48,59.
(3)F(15)=,F(26)=,F(37)=,F(48)==,F(59)=,
因为>>>>,
所以“吉祥数”中,F(t)的最大值为.
因式分解的综合应用
1.
多项式4x2-4与多项式x2-2x+1的公因式是( )
A.
x+1
B.
x-1
C.
x2-1
D.
(x-1)2
2.
(2018·百色)因式分解x-4x3的最后结果是( )
A.
x(1-2x)2
B.
x(2x-1)(2x+1)
C.
x(1-2x)(2x+1)
D.
x(1-4x2)
3.
(2019春·重庆沙坪坝区校级月考)下列因式分解不正确的是( )
A.
3a2b-6ab+3b=3b(a-1)2
B.
-4b2+36a2=4(3a+b)(3a-b)
C.
x2(a-b)-4(b-a)=(a-b)(x+2)(x-2)
D.
(a2+1)2-4a2=(a+1)2(a-1)2
4.
分解因式:
(1)(2019·扬州)a3b-9ab= W.
(2)(2019·广安)3a4-3b4= W.
(3)9x2-(x+2y)2= W.
5.
(1)若mn=3,a+b=4,a-b=5,则mna2-nmb2的值是 W.
(2)(2019·长春一模)若ab=-2,a-3b=5,则a3b-6a2b2+9ab3的值为 W.
6.
(2019春·南京玄武区校级期中)因式分解:
将下列各式因式分解:
(1)16(m+n)2-9(m-n)2;
(2)-8a(a+1)2+2a3;
(3)(x2-2x-2)(x2-2x+4)+9.
12.
若a,b,c是△ABC的三边,试判断代数式(a2+b2-c2)2-4a2b2的值是正数还是负数.
提优测试卷,(时间:90分钟 满分:100分))
一、
选择题(每小题3分,共24分)
1.
若□×3xy=3x2y,则□内应填的单项式是( )
A.
xy
B.
3xy
C.
x
D.
3x
2.
下列各运算中,正确的是( )
A.
(m-2)2=m2-4
B.
(1+2a)2=1+2a+4a2
C.
(a+1)(-a-1)=a2-1
D.
(a+1)(-1+a)=a2-1
3.
已知(x+y)2=7,(x-y)2=5,则xy的值是( )
A.
1
B.
-1
C.
D.
-
4.
(2019春·泰兴期中)若(x2+px+2)(x-3)的乘积中不含x2项,则p的值为( )
A.
3
B.
-3
C.
±3
D.
无法确定
5.
(2019春·盐城大丰区期末)多项式ax2-a与多项式ax2-2ax+a的公因式是( )
A.
a
B.
x-1
C.
a(x-1)
D.
a(x2-1)
6.
(2019春·深圳龙岗区期末)已知a+b=-5,ab=-4,则a2-3ab+b2的值是( )
A.
49
B.
37
C.
45
D.
33
7.
如果257+513能被n整除,则n的值可能是( )
A.
20
B.
30
C.
35
D.
40
8.
(2019春·苏州高新区校级期中)现有一张边长为a的大正方形卡片和三张边长为b的小正方形卡片
(如图①),取出两张小正方形卡片放入“大正方形卡片”内拼成的图案如图②,再重新用两张小正方形卡片放入“大正方形卡片”内拼成的图案如图③.已知图③中阴影部分的面积比图②中阴影部分的面积大2ab-6,则小正方形卡片的面积是( )
A.
2
B.
3
C.
4
D.
5
二、
填空题(每小题3分,共30分)
9.
计算:(1)(2a)3(-3ab2)= ;
(2)x(2x2-3x+1)= ;
(3)(3a+b)(-3a-b)= W.
10.
因式分解:
(1)(2019·沈阳)-x2-4y2+4xy= W.
(2)(2019·宁夏)2a3-8a= W.
11.
(2019春·深圳福田区期末)若mn=1,m-n=2,则m2n-mn2的值是 W.
12.
(2019春·无锡锡山区校级月考)已知三项式9x2+1+是一个完全平方式,但是其中一项看不清了,你认为这一项应该是 (写出一个你认为正确的答案即可).
13.
计算:2342-468×134+1342= W.
14.
已知n为整数,若(2n+1)2-(2n-1)2的值总能被整数m整除,则m的最大值为 W.
15.
(2019春·东台期中)我们规定一种运算:=ad-bc,例如=3×6-4×5=-2.按照这种运算规定,已知=0,则x= W.
16.
从一个边长为2a+b的大正方形中剪出一个边长为b的小正方形,剩余的部分正好能剪拼成四个宽为a的长方形,那么每个长方形的长为 W.
17.
已知a2-2a+b2+4b+5=0,则ab= W.
18.
已知m+=3,则m4+= W.
三、
解答题(共46分)
19.
(8分)(2019春·扬州江都区期中)计算:
(1)(-3a2)2×a4-(-5a4)2;
(2)(2x-y)2-(x-y)(x+y);
(3)(3x+y)2(3x-y)2;
(4)(x+2y+3z)(x+2y-3z).
20.
(8分)因式分解:
(1)3x3-12x2y+12xy2;
(2)a2(x-y)-4x+4y;
(3)(x2+4y2)2-16x2y2;
(4)(x-1)2+2(1-x)·y+y2.
21.
(8分)化简求值:
(1)(a-2b)2+(a-b)(a+b)-2(a-3b)(a-b),其中a=1,b=-2;
(2)已知m+n=3,mn=,求m2+(n-mn)2+2mn-2m2n的值.
23.
(8分)如图,边长为a的正方形ABCD和边长为b(a>b)的正方形CEFG拼在一起,B,C,E三点在同一直线上,设图中阴影部分的面积为S.
(1)如图①,S的值与a的大小有关吗?说明理由.
(2)如图②,若a-b=2,a2+b2=7,求S2的值.
24.
(8分)(枣庄中考题)我们知道,任意一个正整数n都可以进行这样的分解:n=p×q(p,q是正整数,且p≤q),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p×q是n的最佳分解.并规定:F(n)=.
例如12可以分解成1×12,2×6或3×4,因为12-1>6-2>4-3,所以3×4是12的最佳分解,所以F(12)=.
(1)如果一个正整数m是另外一个正整数n的平方,我们称正整数m是完全平方数.试说明对任意一个完全平方数m,总有F(m)=1;
(2)如果一个两位正整数t,t=10x+y(1≤x≤y≤9,x,y为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为36,那么我们称这个数t为“吉祥数”,求所有的“吉祥数”;
(3)在(2)所得“吉祥数”中,求F(t)的最大值.
答案
1.
B 2.
C 3.
C
4.
(1)ab(a+3)(a-3) (2)3(a2+b2)(a+b)(a-b)
(3)4(2x+y)(x-y) 解析:原式=(3x+x+2y)[3x-(x+2y)]=(4x+2y)(2x-2y)=4(2x+y)(x-y).
5.
(1)60 (2)-50
6.
(1)原式=-y(9x2-6xy+y2)=-y(3x-y)2.
(2)原式=m3(a-2)-m(a-2)=m(a-2)(m+1)(m-1).
(3)原式=(9x2-y2)2=(3x+y)2(3x-y)2.
(4)原式=a(x-1)2(x+1)2.
(5)原式=(x2-4x+4)2=(x-2)4.
7.
根据题意,得2a+2b=14,ab=10,
所以a3b+ab3+2a2b2=ab(a2+b2+2ab)=ab(a+b)2=490.
8.
C 解析:原式=2(x+y)(x-y)(a-b),
则呈现的密码信息可能是我爱香港,故选C.
9.
D 解析:由x2-2x-1=0,得到x2=2x+1,x2-2x=1,则原式=2x·x2-7x2+4x-2
019=2x(2x+1)-7(2x+1)+4x-2
019=4x2-8x-7-2
019=4(x2-2x)-2
026=4-2
026=-2
022.故选D.
10.
63,65 解析:248-1=(224+1)(224-1)=(224+1)(212+1)(212-1)=(224+1)(212+1)(26+1)(26-1).因为26=64,所以26-1=63,26+1=65,所以这两个数是63,65.
11.
(1)原式=(4m+4n)2-(3m-3n)2=(4m+4n+3m-3n)(4m+4n-3m+3n)=(7m+n)(m+7n).
(2)原式=2a[a2-4(a+1)2]=2a[a2-(2a+2)2]=2a(a+2a+2)·(a-2a-2)=2a(3a+2)(-a-2)=-2a(3a+2)(a+2).
(3)令x2-2x=t,则
原式=(t-2)(t+4)+9=t2+2t-8+9=t2+2t+1=(t+1)2,
即原式=(x2-2x+1)2=(x-1)4.
12.
原式=(a2+b2-c2+2ab)(a2+b2-c2-2ab)
=[(a+b)2-c2][(a-b)2-c2]
=(a+b+c)(a+b-c)(a-b-c)(a-b+c),
因为a,b,c是△ABC的三边,
所以a+b+c>0,a+b-c>0,a-b-c<0,a-b+c>0,
所以(a+b+c)(a+b-c)(a-b-c)(a-b+c)<0,即原式的值为负数.
13.
【发现】(1)625
(2)a+b=50
【类比】900 说明如下:由题意,得m+n=60,将n=60-m代入mn,
得mn=-m2+60m=-(m-30)2+900,所以当m=30时,mn的最大值为900.
14.
(1)1或- x-1,6x+5 (x-1)(6x+5) 解析:当x=1时,6x2-x-5=0,设6x2-x-5=(x-1)(mx+n),解得m=6,n=5,所以因式分解6x2-x-5=(x-1)(6x+5).
(2)①当x=-1时,2x2+5x+3=0,
所以2x2+5x+3=(x+1)(2x+3).
②当x=1时,x3-7x+6=0,
所以x3-7x+6=(x-1)(x-2)(x+3).
(3)设x3-x2+ax+b=(x2+2x+1)(x+m),
则x3-x2+ax+b=x3+(m+2)x2+(2m+1)x+m,
所以m+2=-1,2m+1=a,m=b,解得a=-5,b=-3,m=-3.
所以x3-x2-5x-3=(x2+2x+1)(x-3)=(x+1)2(x-3).
提优测试卷
1.
C 2.
D 3.
C 4.
A 5.
C 6.
C
7.
B 解析:257+513=514+513=513×(5+1)=513×6=512×30,则n的值可能是30.故选B.
8.
A 解析:题图③中阴影部分的面积为(a-b)2,题图②中阴影部分的面积为(2b-a)2,由题意,得(a-b)2-(2b-a)2=2ab-6,整理,得b2=2,则小正方形卡片的面积是2,故选A.
9.
(1)-24a4b2 (2)2x3-3x2+x (3)-9a2-6ab-b2
10.
(1)-(x-2y)2 (2)2a(a+2)(a-2)
11.
2 12.
6x(答案不唯一) 13.
10
000
14.
8 解析:因为(2n+1)2-(2n-1)2
=(2n+1+2n-1)(2n+1-2n+1)
=4n×2=8n,
所以m的最大值为8.
15.
-
16.
a+b 解析:由题意,得(2a+b)2-b2=(2a+b+b)(2a+b-b)=4a(a+b).故每个长方形的长为a+b.
17.
1 解析:a2-2a+b2+4b+5=a2-2a+1+b2+4b+4=(a-1)2+(b+2)2=0,
所以a-1=0,b+2=0,解得a=1,b=-2,
所以ab=1.
18.
47 解析:m2+=-2·m·=32-2=7,
m4+=-2·m2·=72-2=47.
19.
(1)原式=9a4×a4-25a8=-16a8.
(2)原式=4x2-4xy+y2-x2+y2=3x2-4xy+2y2.
(3)原式=[(3x+y)(3x-y)]2=(9x2-y2)2=81x4-18x2y2+y4.
(4)原式=[(x+2y)+3z][(x+2y)-3z]=(x+2y)2-9z2=x2+4xy+4y2-9z2.
20.
(1)3x(x-2y)2.
(2)(x-y)(a+2)(a-2).
(3)(x+2y)2(x-2y)2.
(4)(x-y-1)2.
21.
(1)原式=a2-4ab+4b2+a2-b2-2(a2-ab-3ab+3b2)=a2-4ab+4b2+a2-b2-2a2+2ab+6ab-6b2=4ab-3b2,
当a=1,b=-2时,原式=4×1×(-2)-3×(-2)2=-8-12=-20.
(2)原式=m2+n2-2mn2+m2n2+2mn-2m2n=(m+n)2+mn(mn-2n-2m)=(m+n)2+mn[mn-2(m+n)],
当m+n=3,mn=时,原式=9+×=.
22.
设67
897=a,则67
898=a+1,67
896=a-1,67
899=a+2,
则67
897×67
898-67
896×67
899
=a(a+1)-(a-1)(a+2)
=(a2+a)-(a2+a-2)
=a2+a-a2-a+2=2.
23.
(1)S的值与a的大小无关,理由如下:
由题意知,S=a2+b2-(a+b)·a-(a-b)·a-b2=b2,
所以S的值与a的大小无关.
(2)因为S=(a-b)·a+(a-b)·b=(a-b)(a+b),
所以S2=(a-b)2(a+b)2.
因为a-b=2,所以(a-b)2=a2-2ab+b2=4.因为a2+b2=7,所以2ab=3,所以(a+b)2=a2+2ab+b2=10,
所以S2=×4×10=10.
24.
(1)对任意一个完全平方数m,设m=n2(n为正整数),
因为|n-n|=0,所以n×n是m的最佳分解,
所以对任意一个完全平方数m,总有F(m)==1.
(2)设交换t的个位上的数与十位上的数得到的新数为t′,
则t′=10y+x.
因为t是“吉祥数”,
所以t′-t=(10y+x)-(10x+y)=9(y-x)=36,
所以y=x+4.
因为1≤x≤y≤9,x,y为自然数,
所以“吉祥数”有15,26,37,48,59.
(3)F(15)=,F(26)=,F(37)=,F(48)==,F(59)=,
因为>>>>,
所以“吉祥数”中,F(t)的最大值为.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
