沪科版数学九上期末复习——解题技巧专题:解决抛物线中与系数a,b,c有关的问题(含答案)
文档属性
| 名称 | 沪科版数学九上期末复习——解题技巧专题:解决抛物线中与系数a,b,c有关的问题(含答案) | 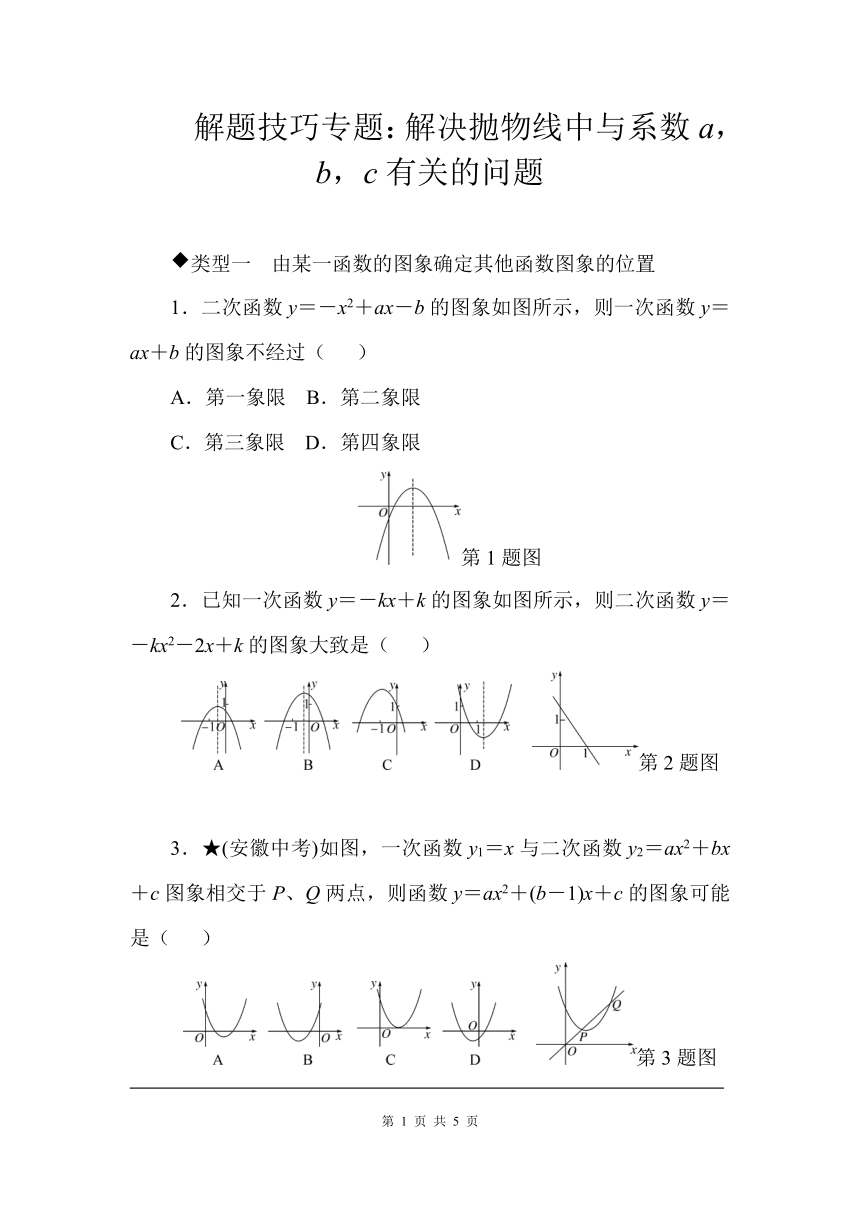 | |
| 格式 | zip | ||
| 文件大小 | 317.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-17 17:28:06 | ||
图片预览


文档简介
解题技巧专题:解决抛物线中与系数a,b,c有关的问题
类型一 由某一函数的图象确定其他函数图象的位置
1.二次函数y=-x2+ax-b的图象如图所示,则一次函数y=ax+b的图象不经过(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
第1题图
2.已知一次函数y=-kx+k的图象如图所示,则二次函数y=-kx2-2x+k的图象大致是(
)
第2题图
3.★(安徽中考)如图,一次函数y1=x与二次函数y2=ax2+bx+c图象相交于P、Q两点,则函数y=ax2+(b-1)x+c的图象可能是(
)
第3题图
类型二 由抛物线的位置确定代数式的符号或未知数的值
4.(安顺中考)如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①a>0;②2a+b=0;③a+b+c>0;④当-1<x<3时,y>0.其中正确的个数为(
)
A.1个
B.2个
C.3个
D.4个
第4题图
第5题图
5.(烟台中考)如图,已知顶点为(-3,-6)的抛物线y=ax2+bx+c经过点(-1,-4),则下列结论中错误的是(
)
A.b2>4ac
B.ax2+bx+c≥-6
C.若点(-2,m),(-5,n)在抛物线上,则m>n
D.关于x的一元二次方程ax2+bx+c=-4的两根为-5和-1
6.(咸宁中考)如图是二次函数y=ax2+bx+c的图象,下列结论:①二次三项式ax2+bx+c的最大值为4;②4a+2b+c<0;③一元二次方程ax2+bx+c=1的两根之和为-1;④使y≤3成立的x的取值范围是x≥0.其中正确的个数有(
)
A.1个
B.2个
C.3个
D.4个
第6题图
第7题图
7.(盘锦中考)如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴是直线x=-2.关于下列结论:①ab<0;②b2-4ac>0;③9a-3b+c<0;④b-4a=0;⑤方程ax2+bx=0的两个根为x1=0,x2=-4.其中正确的结论有(
)
A.①③④
B.②④⑤
C.①②⑤
D.②③⑤
8.★(十堰中考)抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)经过点(-1,0)和(m,0),且1<m<2,当x<-1时,y随着x的增大而减小.下列结论:①abc>0;②a+b>0;③若点A(-3,y1),点B(3,y2)都在抛物线上,则y1<y2;④a(m-1)+b=0;⑤若c≤-1,则b2-4ac≤4a.其中结论错误的是
(填序号).
参考答案:
1.D 2.B
3.A 解析:∵一次函数y1=x与二次函数y2=ax2+bx+c图象相交于P、Q两点,∴方程ax2+(b-1)x+c=0有两个不相等的根,∴函数y=ax2+(b-1)x+c的图象与x轴有两个交点.∵方程ax2+(b-1)x+c=0的两个不相等的根x1>0,x2>0,∴x1+x2=->0,∴->0,∴函数y=ax2+(b-1)x+c的图象的对称轴直线x=->0.∴选项A符合条件.故选A.
4.C 5.C
6.B 解析:∵抛物线的开口向下,顶点坐标为(-1,4),∴二次三项式ax2+bx+c的最大值为4,①正确;∵x=2时,y<0,∴4a+2b+c<0,②正确;根据抛物线的对称性可知,一元二次方程ax2+bx+c=1的两根之和为-2,③错误;使y≤3成立的x的取值范围是x≥0或x≤-2,④错误.故选B.
7.B 解析:∵抛物线开口向下,∴a<0.∵-=-2,∴b=4a,∴b<0,b-4a=0,∴ab>0,∴①错误,④正确;∵抛物线与x轴交于(-4,0),(0,0)两点,∴c=0,b2-4ac>0,∴方程ax2+bx+c=0即ax2+bx=0的两个根为x1=0,x2=-4,∴②⑤正确;∵当x=-3时y>0,即9a-3b+c>0,∴③错误.故正确的结论有②④⑤.故选B.
8.③⑤ 解析:依题意可画出如图所示的图象.∵抛物线开口向上,∴a>0.∵抛物线的对称轴在y轴的右侧,∴->0,∴b<0.∵抛物线与y轴的交点在x轴下方,∴c<0,∴abc>0,①正确;∵抛物线过点(-1,0)和(m,0),且1<m<2,∴0<-<,∴+=>0,∴a+b>0,②正确;∵点A(-3,y1)到对称轴的距离比点B(3,y2)到对称轴的距离远,∴y1>y2,③错误;∵抛物线过点(-1,0),(m,0),∴a-b+c=0,am2+bm+c=0,∴am2-a+bm+b=0,即a(m+1)(m-1)+b(m+1)=0,∴a(m-1)+b=0,④正确;∵<c,而c≤-1,∴<-1,∴b2-4ac>4a,⑤错误.故结论错误的是③⑤.
第
1
页
共
12
页
类型一 由某一函数的图象确定其他函数图象的位置
1.二次函数y=-x2+ax-b的图象如图所示,则一次函数y=ax+b的图象不经过(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
第1题图
2.已知一次函数y=-kx+k的图象如图所示,则二次函数y=-kx2-2x+k的图象大致是(
)
第2题图
3.★(安徽中考)如图,一次函数y1=x与二次函数y2=ax2+bx+c图象相交于P、Q两点,则函数y=ax2+(b-1)x+c的图象可能是(
)
第3题图
类型二 由抛物线的位置确定代数式的符号或未知数的值
4.(安顺中考)如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①a>0;②2a+b=0;③a+b+c>0;④当-1<x<3时,y>0.其中正确的个数为(
)
A.1个
B.2个
C.3个
D.4个
第4题图
第5题图
5.(烟台中考)如图,已知顶点为(-3,-6)的抛物线y=ax2+bx+c经过点(-1,-4),则下列结论中错误的是(
)
A.b2>4ac
B.ax2+bx+c≥-6
C.若点(-2,m),(-5,n)在抛物线上,则m>n
D.关于x的一元二次方程ax2+bx+c=-4的两根为-5和-1
6.(咸宁中考)如图是二次函数y=ax2+bx+c的图象,下列结论:①二次三项式ax2+bx+c的最大值为4;②4a+2b+c<0;③一元二次方程ax2+bx+c=1的两根之和为-1;④使y≤3成立的x的取值范围是x≥0.其中正确的个数有(
)
A.1个
B.2个
C.3个
D.4个
第6题图
第7题图
7.(盘锦中考)如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴是直线x=-2.关于下列结论:①ab<0;②b2-4ac>0;③9a-3b+c<0;④b-4a=0;⑤方程ax2+bx=0的两个根为x1=0,x2=-4.其中正确的结论有(
)
A.①③④
B.②④⑤
C.①②⑤
D.②③⑤
8.★(十堰中考)抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)经过点(-1,0)和(m,0),且1<m<2,当x<-1时,y随着x的增大而减小.下列结论:①abc>0;②a+b>0;③若点A(-3,y1),点B(3,y2)都在抛物线上,则y1<y2;④a(m-1)+b=0;⑤若c≤-1,则b2-4ac≤4a.其中结论错误的是
(填序号).
参考答案:
1.D 2.B
3.A 解析:∵一次函数y1=x与二次函数y2=ax2+bx+c图象相交于P、Q两点,∴方程ax2+(b-1)x+c=0有两个不相等的根,∴函数y=ax2+(b-1)x+c的图象与x轴有两个交点.∵方程ax2+(b-1)x+c=0的两个不相等的根x1>0,x2>0,∴x1+x2=->0,∴->0,∴函数y=ax2+(b-1)x+c的图象的对称轴直线x=->0.∴选项A符合条件.故选A.
4.C 5.C
6.B 解析:∵抛物线的开口向下,顶点坐标为(-1,4),∴二次三项式ax2+bx+c的最大值为4,①正确;∵x=2时,y<0,∴4a+2b+c<0,②正确;根据抛物线的对称性可知,一元二次方程ax2+bx+c=1的两根之和为-2,③错误;使y≤3成立的x的取值范围是x≥0或x≤-2,④错误.故选B.
7.B 解析:∵抛物线开口向下,∴a<0.∵-=-2,∴b=4a,∴b<0,b-4a=0,∴ab>0,∴①错误,④正确;∵抛物线与x轴交于(-4,0),(0,0)两点,∴c=0,b2-4ac>0,∴方程ax2+bx+c=0即ax2+bx=0的两个根为x1=0,x2=-4,∴②⑤正确;∵当x=-3时y>0,即9a-3b+c>0,∴③错误.故正确的结论有②④⑤.故选B.
8.③⑤ 解析:依题意可画出如图所示的图象.∵抛物线开口向上,∴a>0.∵抛物线的对称轴在y轴的右侧,∴->0,∴b<0.∵抛物线与y轴的交点在x轴下方,∴c<0,∴abc>0,①正确;∵抛物线过点(-1,0)和(m,0),且1<m<2,∴0<-<,∴+=>0,∴a+b>0,②正确;∵点A(-3,y1)到对称轴的距离比点B(3,y2)到对称轴的距离远,∴y1>y2,③错误;∵抛物线过点(-1,0),(m,0),∴a-b+c=0,am2+bm+c=0,∴am2-a+bm+b=0,即a(m+1)(m-1)+b(m+1)=0,∴a(m-1)+b=0,④正确;∵<c,而c≤-1,∴<-1,∴b2-4ac>4a,⑤错误.故结论错误的是③⑤.
第
1
页
共
12
页
