北师大版七年级数学下册:4.3 探索三角形全等的条件 课件(共45张PPT)
文档属性
| 名称 | 北师大版七年级数学下册:4.3 探索三角形全等的条件 课件(共45张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-17 00:00:00 | ||
图片预览









文档简介
(共45张PPT)
2.
叫做全等三角形。
1.能够重合的两个图形叫做
。
全等形
4.全等三角形的
和
相等
对应边
对应角
对应顶点
能够重合的两个三角形
3.“全等”用符号“
”来表示,读作“
”
对应边
对应角
5.书写全等式时要求把对应字母放在对应
的位置上
全等于
≌
如图:△AOD≌△BOC,写出其中相等的角
A
D
C
B
O
解:∠A=∠B
∠D=∠C
∠DOA=∠COB
如图,若△ABC≌△EFC,且CF=3cm,∠EFC=64°,
则BC=_____cm,∠B=_____.
3
64°
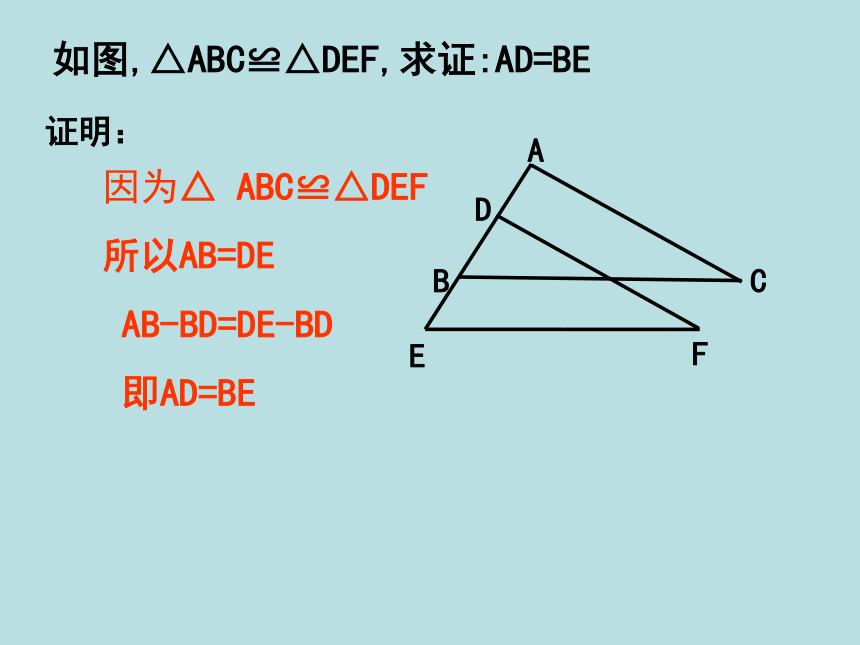
如图,△ABC≌△DEF,求证:AD=BE
B
A
E
F
C
D
第1课时
3
探索三角形全等的条件
1.会用“边边边”判定三角形全等.
2.经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程.
3.三角形的稳定性.
在数学这门科学里,我们发现真理的主要工具是归纳和类比.
——拉普拉斯
要画一个三角形与小明画的三角形全等,需要几个与边或角的大小有关的条件呢?
想一想
问题一:
如果两个三角形中上述六个元素对应相等,是否一定全等?
问题二:
两个三角形全等,是否一定需要六个条件呢?如果只满足上述一部分条件,是否也能说明它们全等?
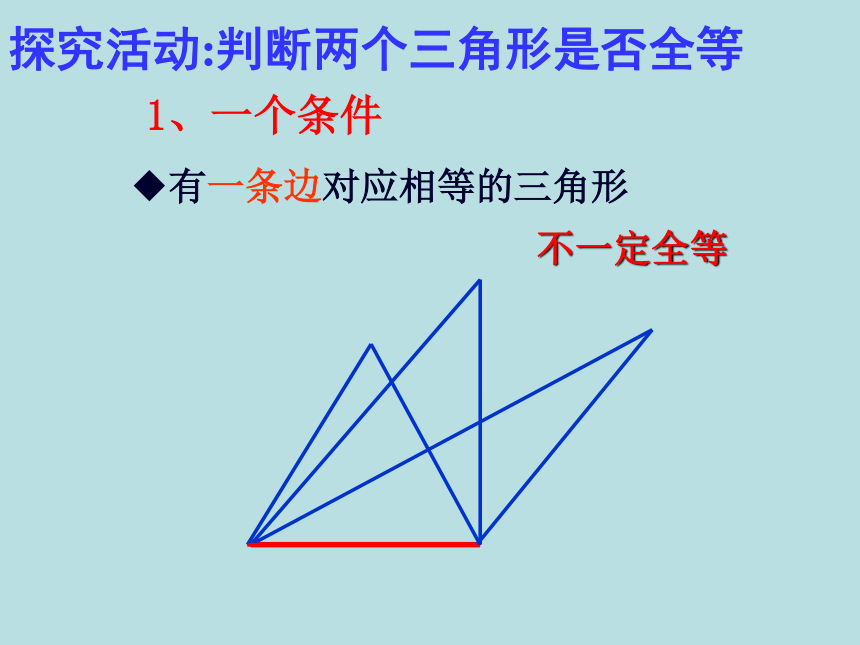
1、一个条件
有一条边对应相等的三角形
不一定全等
探究活动:判断两个三角形是否全等
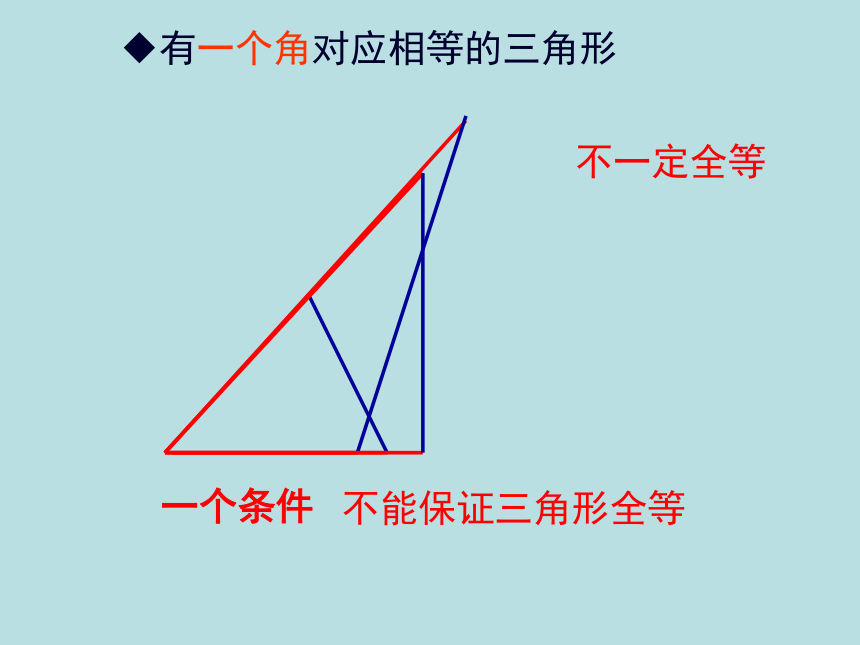
有一个角对应相等的三角形
不一定全等
一个条件
不能保证三角形全等
2、按照下面给出的两个条件画出三角形,并与其他同学的比一比
(3)三角形的一个角为
30°,一条边为6cm
;
探究活动
(2)三角形的两条边分别是
4cm
和
6cm
;
(1)三角形的两个角分别是
30°和
60°.
(1)三角形的两个角分别是:30°,60°
不一定全等
结论:
有两个条件对应相等不能
保证三角形全等
(2)三角形的两条边分别是:4cm,6cm
不一定全等
(3)
三角形的一个角为30°,一条边为6cm
不一定全等
2.
给出两个条件画三角形时,有几种可能的情况?每种情况下作出的三角形一定全等吗?分别按照下面的条件做一做。
做一做
1.
只给一个条件(一条边或一个角)画三角形时,大家画出的三角形一定全等吗?
不一定全等
(3)
三角形的两条边分别为4cm,6cm.
(1)
三角形的一个内角为30°,一条边为3cm;
(2)
三角形的两个内角分别为30°和
50°;
不一定全等
议一议
如果给出三个条件画三角形,你能说出有哪几种可能的情况吗?
1.三个角
2.三条边
3.两边一角
4.两角一边
做一做
(1)
已知一个三角形的三个内角分别为40°,60°和80°,你能画出这个三角形吗?把你画的三角形与同伴画出的进行比较,它们一定全等吗?
三个内角对应相等的两个三角形不一定全等
(1)已知三角形的三个角分别为30°、60°、90°
三个内角对应相等的三角形不一定全等。
探究活动
3、三个条件
结论
做一做
(2)
已知一个三角形的三条边分别为4cm,5cm和7cm,你能画出这个三角形吗?把你画的三角形与同伴画出的进行比较,它们一定全等吗?
任意画一个△ABC,再画一个△A′B′C′,使AB=A′B′,BC=B′C′,CA=C′A′,判断两个三角形是否全等.
作法:1、画线段A′B′=AB;
2、分别以A′、B′为圆心,以线段AC、BC为半径作弧,两弧交于点C′;
3、连接线段B′C′,A′C′.
A?
B?
C?
三边对应相等的两个三角形全等,简写为“边边边”或“SSS”。
AB=A’B’
BC=B’C’
AC=A’C’
(SSS)
数学表达式:
在△ABC和△A'B'C'中
BC
CB
△DCB
BF=CD
或
BD=CF
所以
△ABD
≌△CDB
3.如图,在四边形ABCD中AB=CD,AD=BC,则∠A=∠C.请说明理由.
解析:在△ABD和△CDB中
AB=CD
(已知)
AD=CB
(已知)
BD=DB
(公共边)
(SSS)
所以
∠A=
∠C(
)
全等三角形的对应角相等
证明:因为
D是BC的中点
所以
BD=CD
在△ABD和△ACD中,
AB=AC
(已知)
BD=CD
(已证)
AD=AD
(公共边)
所以
△ABD
≌
△ACD
(SSS)
因为
【例】如图,△ABC是一个钢架,AB=AC,AD是连接A与BC
中点D的支架.
求证:△ABD≌
△ACD.
(1)准备条件:证全等时要用的间接条件要先证好;
(2)三角形全等书写三步骤:
①写出在哪两个三角形中;
②摆出三个条件用大括号括起来;
③写出全等结论.
证明的书写步骤:
如图,已知AB=CD,BC=DA。你能说明△ABC与△CDA全等吗?你能说明AB∥CD,AD∥BC吗?为什么?
D
B
A
C
解:在△ABC与△CDA中,
∵
∴△ABC≌△CDA(SSS)
∴∠BAC=∠DCA,∠ACB=∠CAD(全等三角形对应角相等)
∴AB∥CD,AD∥BC(内错角相等,两直线平行)
练习1.
1.
两个锐角对应相等的两个直角三角形全等吗?为什么?
不一定全等
解:
A
B
C
D
E
F
RtΔABC和RtΔDEF不全等
3.
已知:如图AB=CD,AD=BC.则∠A与∠C相等吗?为什么?
练习2.
解:
∠A=∠C.
连接BD.
因为AB=CD,AD=CB,BD=DB
所以ΔABD≌ΔCDB
所以∠A=∠C.
三角形的稳定性
三角形具有稳定性,
四边形不具有稳定性.
盖房子时,在窗框未安装好之前,木工师傅常常先在窗框上斜钉一根木条,为什么要这样做呢?
三角形的稳定性
将四边形木架上再钉一根木条,将它的一对顶点连接起来,然后再扭动它,这时木架的形状还会改变吗?为什么?
不会,三角形具有稳定性.
斜梁
斜梁
直
梁
三角形的稳定性
如图,工人师傅砌门时,常用木条EF固定门框ABCD,使其不变形,这种做法根据的是三角形的稳定性.
三角形的稳定性
四边形不稳定性的应用
活动挂衣架
1.下列图形中具有稳定性的是(
)
(A)正方形
(B)长方形
(C)直角三角形
(D)平行四边形
C
2.要使下列木架稳定各至少需要多少根木棍?
一根
两根
三根
1.如图,AB=AC,AE=AD,BD=CE,
求证:△AEB
≌
△
ADC.
【解析】
因为BD=CE,所以
BD-ED=CE-ED,所以BE=CD.
2.已知AC=FE,BC=DE,点A,D,B,F在一条直线上,AD=FB(如图),要用“边边边”证明△ABC
≌△
FDE,除了已知中的AC=FE,BC=DE以外,还应该有什么条件?怎样才能得到这个条件?
【解析】要说明△ABC
≌△FDE,还应该有AB=FD这个条件.
因为DB是AB与DF的公共部分,且AD=BF
所以AD+DB=BF+DB
即AB=FD
3.(昆明·中考)如图,点B,D,C,F在一条直线上,且BC=FD,AB=EF.
(1)请你只添加一个条件(不再加辅助线),
使△ABC≌△EFD,你添加的条件是
;
(2)添加了条件后,证明△ABC≌△EFD.
AC=ED
(2)在△
ABC和△
EFD中,
AB=EF
BC=FD
AC=ED
所以△ABC≌△EFD(SSS)
课内链接
2.
已知:如图AB=CD,AD=BC,E,F是BD上两点,且AE=CF,DE=BF,那么图中共有几对全等的三角形?说明理由.
分析:可先通过观察,初步判断有哪几对三角形全等,然后再根据条件判断。
解:
图中共有3对全等的三角形.
通过本课时的学习,需要我们掌握:
1.三角形全等的判定定理一——SSS.
2.利用它可以证明简单的三角形全等问题.
3.三角形具有稳定性。
1、如图,AB=AC,BD=CD,BH=CH,图中有几组全等的三角形?它们全等的条件是什么?
2
如图,已知AB=CD,BC=DA。你能说明△ABC与△CDA全等吗?你能说明AB∥CD,AD∥BC吗?为什么?
H
D
C
B
A
解:有三组。 在△ABH和△ACH中
∵AB=AC,BH=CH,AH=AH ∴△ABH≌△ACH(SSS);在△ABH和△ACH中∵AB=AC,BD=CD,AD=AD ∴△ABD≌△ACD(SSS);在△ABH和△ACH中
∵BD=CD,BH=CH,DH=DH
∴△DBH≌△DCH(SSS)
D
B
A
C
解:在△ABC与△CDA中,
∵
∴△ABC≌△CDA(SSS)
∴∠BAC=∠DCA,∠ACB=∠CAD(全等三角形对应角相等)
∴AB∥CD,AD∥BC(内错角相等,两直线平行)
解析:△ABC≌△DCB
理由如下:
AB
=
DC
AC
=
DB
△ABC≌
1.如图,AB=CD,AC=BD,△ABC和△DCB是否全等?
△DCB
BC=
CB
BF=CD
或BD=CF
(SSS)
2.
叫做全等三角形。
1.能够重合的两个图形叫做
。
全等形
4.全等三角形的
和
相等
对应边
对应角
对应顶点
能够重合的两个三角形
3.“全等”用符号“
”来表示,读作“
”
对应边
对应角
5.书写全等式时要求把对应字母放在对应
的位置上
全等于
≌
如图:△AOD≌△BOC,写出其中相等的角
A
D
C
B
O
解:∠A=∠B
∠D=∠C
∠DOA=∠COB
如图,若△ABC≌△EFC,且CF=3cm,∠EFC=64°,
则BC=_____cm,∠B=_____.
3
64°
如图,△ABC≌△DEF,求证:AD=BE
B
A
E
F
C
D
第1课时
3
探索三角形全等的条件
1.会用“边边边”判定三角形全等.
2.经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程.
3.三角形的稳定性.
在数学这门科学里,我们发现真理的主要工具是归纳和类比.
——拉普拉斯
要画一个三角形与小明画的三角形全等,需要几个与边或角的大小有关的条件呢?
想一想
问题一:
如果两个三角形中上述六个元素对应相等,是否一定全等?
问题二:
两个三角形全等,是否一定需要六个条件呢?如果只满足上述一部分条件,是否也能说明它们全等?
1、一个条件
有一条边对应相等的三角形
不一定全等
探究活动:判断两个三角形是否全等
有一个角对应相等的三角形
不一定全等
一个条件
不能保证三角形全等
2、按照下面给出的两个条件画出三角形,并与其他同学的比一比
(3)三角形的一个角为
30°,一条边为6cm
;
探究活动
(2)三角形的两条边分别是
4cm
和
6cm
;
(1)三角形的两个角分别是
30°和
60°.
(1)三角形的两个角分别是:30°,60°
不一定全等
结论:
有两个条件对应相等不能
保证三角形全等
(2)三角形的两条边分别是:4cm,6cm
不一定全等
(3)
三角形的一个角为30°,一条边为6cm
不一定全等
2.
给出两个条件画三角形时,有几种可能的情况?每种情况下作出的三角形一定全等吗?分别按照下面的条件做一做。
做一做
1.
只给一个条件(一条边或一个角)画三角形时,大家画出的三角形一定全等吗?
不一定全等
(3)
三角形的两条边分别为4cm,6cm.
(1)
三角形的一个内角为30°,一条边为3cm;
(2)
三角形的两个内角分别为30°和
50°;
不一定全等
议一议
如果给出三个条件画三角形,你能说出有哪几种可能的情况吗?
1.三个角
2.三条边
3.两边一角
4.两角一边
做一做
(1)
已知一个三角形的三个内角分别为40°,60°和80°,你能画出这个三角形吗?把你画的三角形与同伴画出的进行比较,它们一定全等吗?
三个内角对应相等的两个三角形不一定全等
(1)已知三角形的三个角分别为30°、60°、90°
三个内角对应相等的三角形不一定全等。
探究活动
3、三个条件
结论
做一做
(2)
已知一个三角形的三条边分别为4cm,5cm和7cm,你能画出这个三角形吗?把你画的三角形与同伴画出的进行比较,它们一定全等吗?
任意画一个△ABC,再画一个△A′B′C′,使AB=A′B′,BC=B′C′,CA=C′A′,判断两个三角形是否全等.
作法:1、画线段A′B′=AB;
2、分别以A′、B′为圆心,以线段AC、BC为半径作弧,两弧交于点C′;
3、连接线段B′C′,A′C′.
A?
B?
C?
三边对应相等的两个三角形全等,简写为“边边边”或“SSS”。
AB=A’B’
BC=B’C’
AC=A’C’
(SSS)
数学表达式:
在△ABC和△A'B'C'中
BC
CB
△DCB
BF=CD
或
BD=CF
所以
△ABD
≌△CDB
3.如图,在四边形ABCD中AB=CD,AD=BC,则∠A=∠C.请说明理由.
解析:在△ABD和△CDB中
AB=CD
(已知)
AD=CB
(已知)
BD=DB
(公共边)
(SSS)
所以
∠A=
∠C(
)
全等三角形的对应角相等
证明:因为
D是BC的中点
所以
BD=CD
在△ABD和△ACD中,
AB=AC
(已知)
BD=CD
(已证)
AD=AD
(公共边)
所以
△ABD
≌
△ACD
(SSS)
因为
【例】如图,△ABC是一个钢架,AB=AC,AD是连接A与BC
中点D的支架.
求证:△ABD≌
△ACD.
(1)准备条件:证全等时要用的间接条件要先证好;
(2)三角形全等书写三步骤:
①写出在哪两个三角形中;
②摆出三个条件用大括号括起来;
③写出全等结论.
证明的书写步骤:
如图,已知AB=CD,BC=DA。你能说明△ABC与△CDA全等吗?你能说明AB∥CD,AD∥BC吗?为什么?
D
B
A
C
解:在△ABC与△CDA中,
∵
∴△ABC≌△CDA(SSS)
∴∠BAC=∠DCA,∠ACB=∠CAD(全等三角形对应角相等)
∴AB∥CD,AD∥BC(内错角相等,两直线平行)
练习1.
1.
两个锐角对应相等的两个直角三角形全等吗?为什么?
不一定全等
解:
A
B
C
D
E
F
RtΔABC和RtΔDEF不全等
3.
已知:如图AB=CD,AD=BC.则∠A与∠C相等吗?为什么?
练习2.
解:
∠A=∠C.
连接BD.
因为AB=CD,AD=CB,BD=DB
所以ΔABD≌ΔCDB
所以∠A=∠C.
三角形的稳定性
三角形具有稳定性,
四边形不具有稳定性.
盖房子时,在窗框未安装好之前,木工师傅常常先在窗框上斜钉一根木条,为什么要这样做呢?
三角形的稳定性
将四边形木架上再钉一根木条,将它的一对顶点连接起来,然后再扭动它,这时木架的形状还会改变吗?为什么?
不会,三角形具有稳定性.
斜梁
斜梁
直
梁
三角形的稳定性
如图,工人师傅砌门时,常用木条EF固定门框ABCD,使其不变形,这种做法根据的是三角形的稳定性.
三角形的稳定性
四边形不稳定性的应用
活动挂衣架
1.下列图形中具有稳定性的是(
)
(A)正方形
(B)长方形
(C)直角三角形
(D)平行四边形
C
2.要使下列木架稳定各至少需要多少根木棍?
一根
两根
三根
1.如图,AB=AC,AE=AD,BD=CE,
求证:△AEB
≌
△
ADC.
【解析】
因为BD=CE,所以
BD-ED=CE-ED,所以BE=CD.
2.已知AC=FE,BC=DE,点A,D,B,F在一条直线上,AD=FB(如图),要用“边边边”证明△ABC
≌△
FDE,除了已知中的AC=FE,BC=DE以外,还应该有什么条件?怎样才能得到这个条件?
【解析】要说明△ABC
≌△FDE,还应该有AB=FD这个条件.
因为DB是AB与DF的公共部分,且AD=BF
所以AD+DB=BF+DB
即AB=FD
3.(昆明·中考)如图,点B,D,C,F在一条直线上,且BC=FD,AB=EF.
(1)请你只添加一个条件(不再加辅助线),
使△ABC≌△EFD,你添加的条件是
;
(2)添加了条件后,证明△ABC≌△EFD.
AC=ED
(2)在△
ABC和△
EFD中,
AB=EF
BC=FD
AC=ED
所以△ABC≌△EFD(SSS)
课内链接
2.
已知:如图AB=CD,AD=BC,E,F是BD上两点,且AE=CF,DE=BF,那么图中共有几对全等的三角形?说明理由.
分析:可先通过观察,初步判断有哪几对三角形全等,然后再根据条件判断。
解:
图中共有3对全等的三角形.
通过本课时的学习,需要我们掌握:
1.三角形全等的判定定理一——SSS.
2.利用它可以证明简单的三角形全等问题.
3.三角形具有稳定性。
1、如图,AB=AC,BD=CD,BH=CH,图中有几组全等的三角形?它们全等的条件是什么?
2
如图,已知AB=CD,BC=DA。你能说明△ABC与△CDA全等吗?你能说明AB∥CD,AD∥BC吗?为什么?
H
D
C
B
A
解:有三组。 在△ABH和△ACH中
∵AB=AC,BH=CH,AH=AH ∴△ABH≌△ACH(SSS);在△ABH和△ACH中∵AB=AC,BD=CD,AD=AD ∴△ABD≌△ACD(SSS);在△ABH和△ACH中
∵BD=CD,BH=CH,DH=DH
∴△DBH≌△DCH(SSS)
D
B
A
C
解:在△ABC与△CDA中,
∵
∴△ABC≌△CDA(SSS)
∴∠BAC=∠DCA,∠ACB=∠CAD(全等三角形对应角相等)
∴AB∥CD,AD∥BC(内错角相等,两直线平行)
解析:△ABC≌△DCB
理由如下:
AB
=
DC
AC
=
DB
△ABC≌
1.如图,AB=CD,AC=BD,△ABC和△DCB是否全等?
△DCB
BC=
CB
BF=CD
或BD=CF
(SSS)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
