人教版高二物理选修3-1 3.6带电粒子在匀强磁场中的运动--带电粒子在有界磁场中的临界极值问题 (共21张PPT)
文档属性
| 名称 | 人教版高二物理选修3-1 3.6带电粒子在匀强磁场中的运动--带电粒子在有界磁场中的临界极值问题 (共21张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-06-17 00:00:00 | ||
图片预览




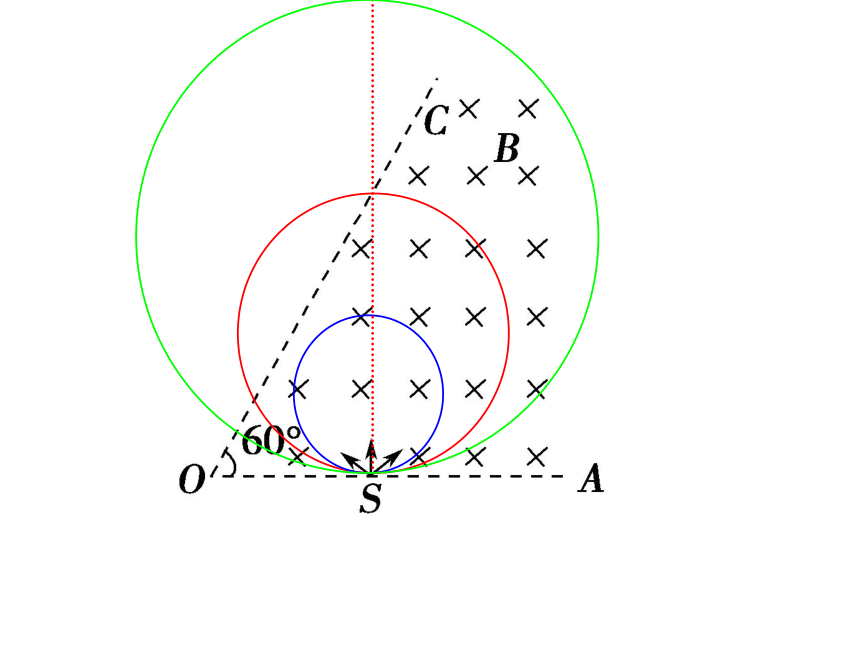
文档简介
(共21张PPT)
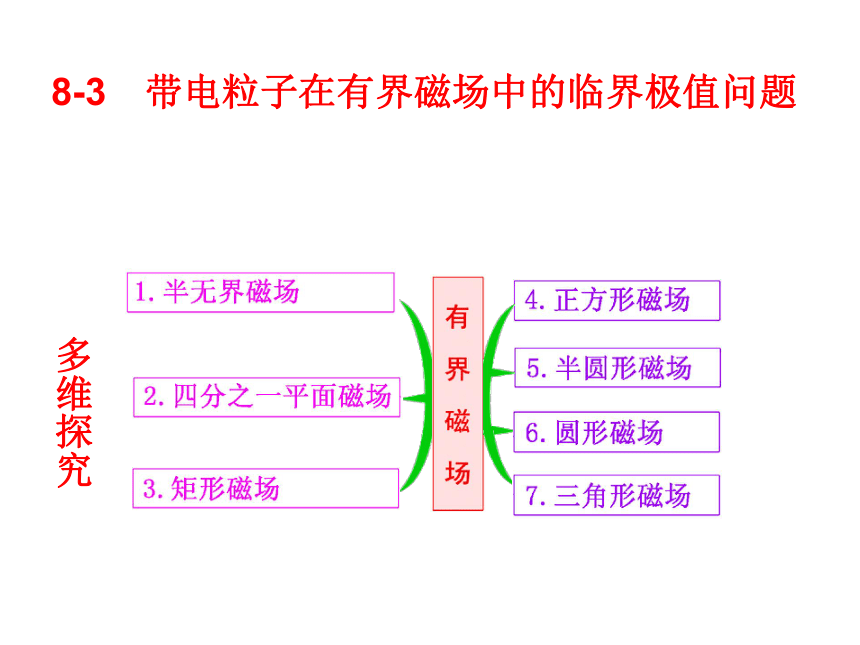
8-3 带电粒子在有界磁场中的临界极值问题
多维探究
例1.在真空中宽d的区域内有匀强磁场B,质量为m,电量为e,速率为v的电子从边界CD外侧垂直射入磁场,入射方向与CD夹角θ,为了使电子能从磁场的另一侧边界EF射出,v应满足的条件是:
A.v>eBd/m(1+sinθ)
B.v>eBd/m(1+cosθ)
C.v>
eBd/msinθ
D.v<
eBd/mcosθ
B
思考:求电子在磁场中运动的最长时间是多长?
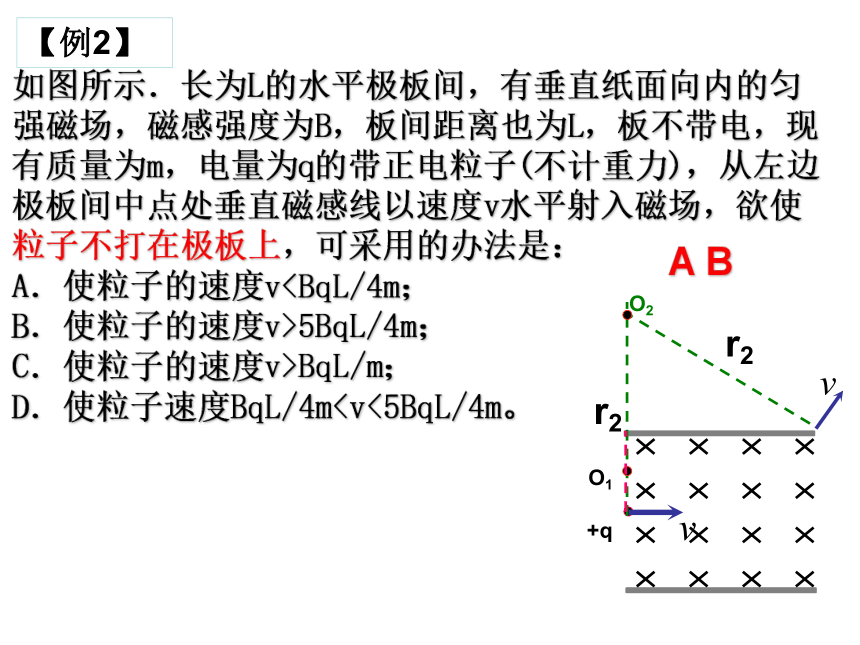
如图所示.长为L的水平极板间,有垂直纸面向内的匀强磁场,磁感强度为B,板间距离也为L,板不带电,现有质量为m,电量为q的带正电粒子(不计重力),从左边极板间中点处垂直磁感线以速度v水平射入磁场,欲使粒子不打在极板上,可采用的办法是:
A.使粒子的速度vB.使粒子的速度v>5BqL/4m;
C.使粒子的速度v>BqL/m;
D.使粒子速度BqL/4mr2
+q
r2
A
B
【例2】
r2
+q
r2
粒子擦着上板从左边穿出时,圆心在O1点,有
粒子擦着上板从右边穿出时,圆心在O2点,有
粒子不打在极板上可能从左端穿出,也可能从右端穿出,必须全面分析问题.
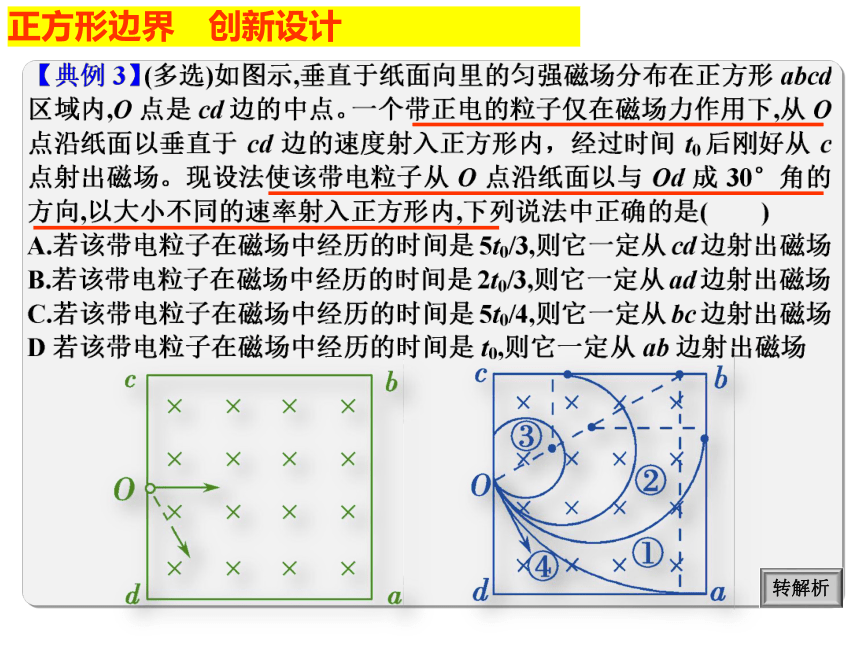
正方形边界
创新设计
2R
R
2R
M
N
O
s
a
b
P1
P2
N
L
磁聚焦概括:
平行会聚于一点
一点发散成平行
区域半径
R
与运动半径
r
相等
迁移与逆向、对称的物理思想!
●高考命题第25题特色
[2010·课标全国卷]
难度系数:0.134
难在准确画出轨迹和几何知识的应用
关键词:带正电离子、速度大小相同、半径R、在a/2-a之间、全部、恰好
画粒子沿+y方向以>a/2为半径做圆周运动的轨迹
将运动圆弧以O为圆心旋转
圆弧轨迹与磁场上边界相切时为临界轨迹.
比较圆心角的大小?找到最长运动时间
读题
画图
旋转
找临界
比较
O1
O2
审题析疑
答题的科学素养
基础知识、基本技能
隐含条件,确定粒子运动轨迹
应用数学知识处理物理问题的能力
运算能力
(2009年海南物理16题)
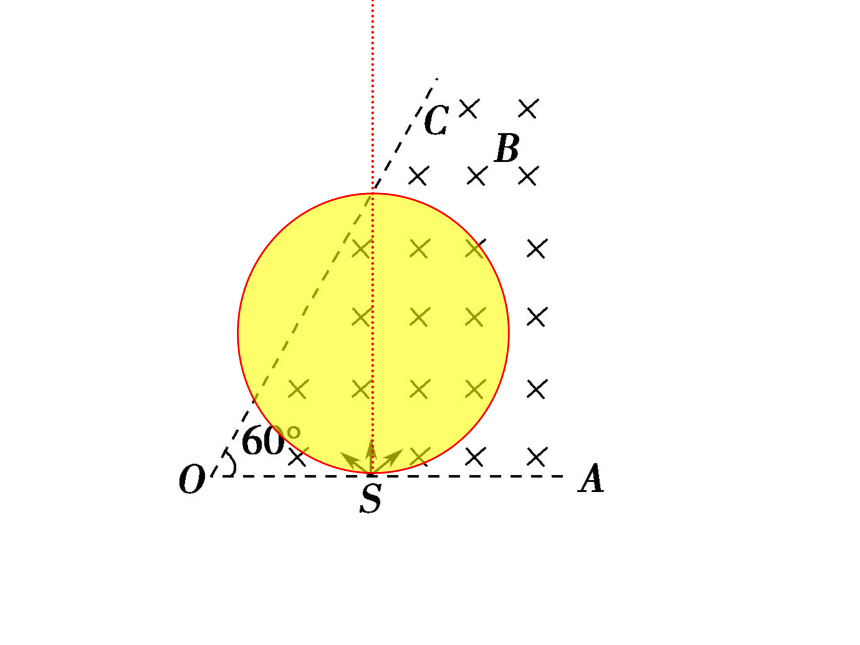
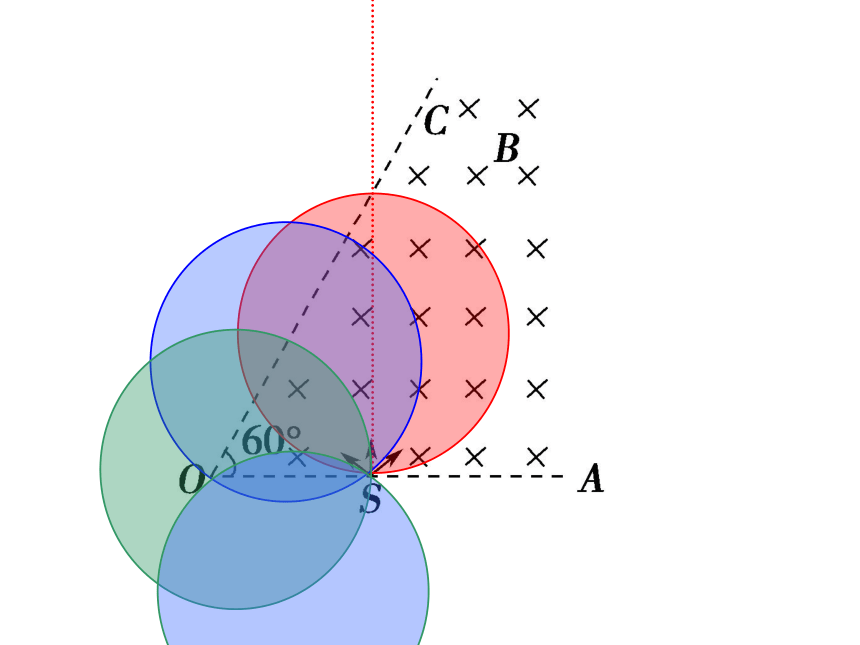
如图,ABCD是边长为a
的正方形。质量为m、电荷量为e
的电子以大小为v0
的初速度沿纸面垂直于BC边射入正方形区域。在正方形内适当区域中有匀强磁场。电子从BC边上的任意点入射,都只能从A
点射出磁场。不计重力,求:
(1)此匀强磁场区域中磁感应强度的方向和大小;
(2)此匀强磁场区域的最小面积。
E
数学中的函数方程
用函数分析、表达物理问题
例5.如图所示,虚线所围区域内有方向垂直纸面向里的匀强磁场,磁感应强度为B。一束电子沿圆形区域的直径方向以速度v射入磁场,电子束经过磁场区后,其运动的方向与原入射方向成θ角。设电子质量为m,电荷量为e,不计电子之间的相互作用力及所受的重力。求:
(1)电子在磁场中运动轨迹的半径R;
(2)电子在磁场中运动的时间t;
(3)圆形磁场区域的半径r。
解:
(1)由牛顿第二定律和洛沦兹力公式得
解得
(2)设电子做匀速圆周运动的周期为T,
由如图所示的几何关系得:圆心角
所以
(3)由如图所示几何关系可知,
所以
则
8-3 带电粒子在有界磁场中的临界极值问题
多维探究
例1.在真空中宽d的区域内有匀强磁场B,质量为m,电量为e,速率为v的电子从边界CD外侧垂直射入磁场,入射方向与CD夹角θ,为了使电子能从磁场的另一侧边界EF射出,v应满足的条件是:
A.v>eBd/m(1+sinθ)
B.v>eBd/m(1+cosθ)
C.v>
eBd/msinθ
D.v<
eBd/mcosθ
B
思考:求电子在磁场中运动的最长时间是多长?
如图所示.长为L的水平极板间,有垂直纸面向内的匀强磁场,磁感强度为B,板间距离也为L,板不带电,现有质量为m,电量为q的带正电粒子(不计重力),从左边极板间中点处垂直磁感线以速度v水平射入磁场,欲使粒子不打在极板上,可采用的办法是:
A.使粒子的速度v
C.使粒子的速度v>BqL/m;
D.使粒子速度BqL/4m
+q
r2
A
B
【例2】
r2
+q
r2
粒子擦着上板从左边穿出时,圆心在O1点,有
粒子擦着上板从右边穿出时,圆心在O2点,有
粒子不打在极板上可能从左端穿出,也可能从右端穿出,必须全面分析问题.
正方形边界
创新设计
2R
R
2R
M
N
O
s
a
b
P1
P2
N
L
磁聚焦概括:
平行会聚于一点
一点发散成平行
区域半径
R
与运动半径
r
相等
迁移与逆向、对称的物理思想!
●高考命题第25题特色
[2010·课标全国卷]
难度系数:0.134
难在准确画出轨迹和几何知识的应用
关键词:带正电离子、速度大小相同、半径R、在a/2-a之间、全部、恰好
画粒子沿+y方向以>a/2为半径做圆周运动的轨迹
将运动圆弧以O为圆心旋转
圆弧轨迹与磁场上边界相切时为临界轨迹.
比较圆心角的大小?找到最长运动时间
读题
画图
旋转
找临界
比较
O1
O2
审题析疑
答题的科学素养
基础知识、基本技能
隐含条件,确定粒子运动轨迹
应用数学知识处理物理问题的能力
运算能力
(2009年海南物理16题)
如图,ABCD是边长为a
的正方形。质量为m、电荷量为e
的电子以大小为v0
的初速度沿纸面垂直于BC边射入正方形区域。在正方形内适当区域中有匀强磁场。电子从BC边上的任意点入射,都只能从A
点射出磁场。不计重力,求:
(1)此匀强磁场区域中磁感应强度的方向和大小;
(2)此匀强磁场区域的最小面积。
E
数学中的函数方程
用函数分析、表达物理问题
例5.如图所示,虚线所围区域内有方向垂直纸面向里的匀强磁场,磁感应强度为B。一束电子沿圆形区域的直径方向以速度v射入磁场,电子束经过磁场区后,其运动的方向与原入射方向成θ角。设电子质量为m,电荷量为e,不计电子之间的相互作用力及所受的重力。求:
(1)电子在磁场中运动轨迹的半径R;
(2)电子在磁场中运动的时间t;
(3)圆形磁场区域的半径r。
解:
(1)由牛顿第二定律和洛沦兹力公式得
解得
(2)设电子做匀速圆周运动的周期为T,
由如图所示的几何关系得:圆心角
所以
(3)由如图所示几何关系可知,
所以
则
