人教版数学八年级下册 18.1 平行四边形 同步练习(含答案)
文档属性
| 名称 | 人教版数学八年级下册 18.1 平行四边形 同步练习(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 109.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-17 00:00:00 | ||
图片预览




文档简介
平行四边形
同步练习
选择题
1、下列特征中,平行四边形不一定具有的是(
)
A.邻角互补?????
B.对角互补?????
C.对角相等??????
D.内角和为360°
2、四边形ABCD中,对角线AC与BD交于点O,下列条件中不一定能判定这个四边形是平行四边形的是( )
A.AB∥DC,AD=BC?
B.AD∥BC,AB∥DC
C.AB=DC,AD=BC???
D.OA=OC,OB=OD
3、下列条件中能判定四边形ABCD是平行四边形的是( )
A.∠A=∠B,∠C=∠D
B.AB=AD,CB=CD
C.AB=CD,AD=BC
D.AB∥CD,AD=BC
4、如图,在平行四边形ABCD中,AB=4,BC=6,AC的垂直平分线交AD于点E,则△CDE的周长是( )
A.7??????
B.10????
C.11????
D.12
5、如图,?ABCD中,E,F是对角线BD上的两点,如果添加一个条件,使△ABE≌△CDF,则添加的条件不能为( )
A.BE=DF B.BF=DE C.AE=CF D.∠1=∠2
6、在平面直角坐标系中,□ABCD的顶点A(0,0),B(5,0),D(2,
3),则顶点C的坐标是(?????
)
A、(3,7)????
B、(5,3)?????
C、(7,3)????
D、(8,2)
7、如图,在?ABCD中,E、F、G、H分别是各边的中点,在下列四个图形中,阴影部分的面积与其他三个阴影部分面积不相等的是( )
A.??
B.?
C.
D.
8、如图,在平行四边形ABCD中,过点C的直线CE⊥AB,垂足为E,若∠EAD=53°,则∠BCE的度数为(????
)
A.53°??
B.37°???
C.47°??
D.123°
9、平行四边形的周长为240,两邻边长为x、y,则y与x之间的关系是(????
)
A.y=120﹣x(0<x<120)???
B.y=120﹣x(0≤x≤120)
C.y=240﹣x(0<x<240)???
D.y=240﹣x(0≤x≤240)
10、平行四边形ABCD的周长为2a,两条对角线相交于O,△AOB的周长比△BOC的周长大b,则AB的长为( )
A.???
B.
C.??
?
D.
11、.如图:在?ABCD中,AE⊥BC于E,AF⊥CD于F.若AE=4,AF=6,且?ABCD的周长为30,则ABCD的面积为( )
A.24??
B.36??
C.40??
D.48
12、如图,平行四边形ABCD中,AE平分∠BAD,交BC于点E,且AB=AE,延长AB与DE的延长线交于点F.下列结论中:
①△ABC≌△EAD;②△ABE是等边三角形;③AD=AF;④S△ABE=S△CDE;⑤S△ABE=S△CEF.
其中正确的是( )
A.①②③????
B.①②④????
C.①②⑤????
D.①③④
二、填空题
13、如图,平行四边形ABCD中,、分别为、边上的点,要使需添加一个条件:?????????
.
14、在平行四边形ABCD中,∠A+∠C=100°,则∠A=???
,∠B=???
?.
15、如图,在平行四边形ABCD中,DB=DC、,CEBD于E,则???????
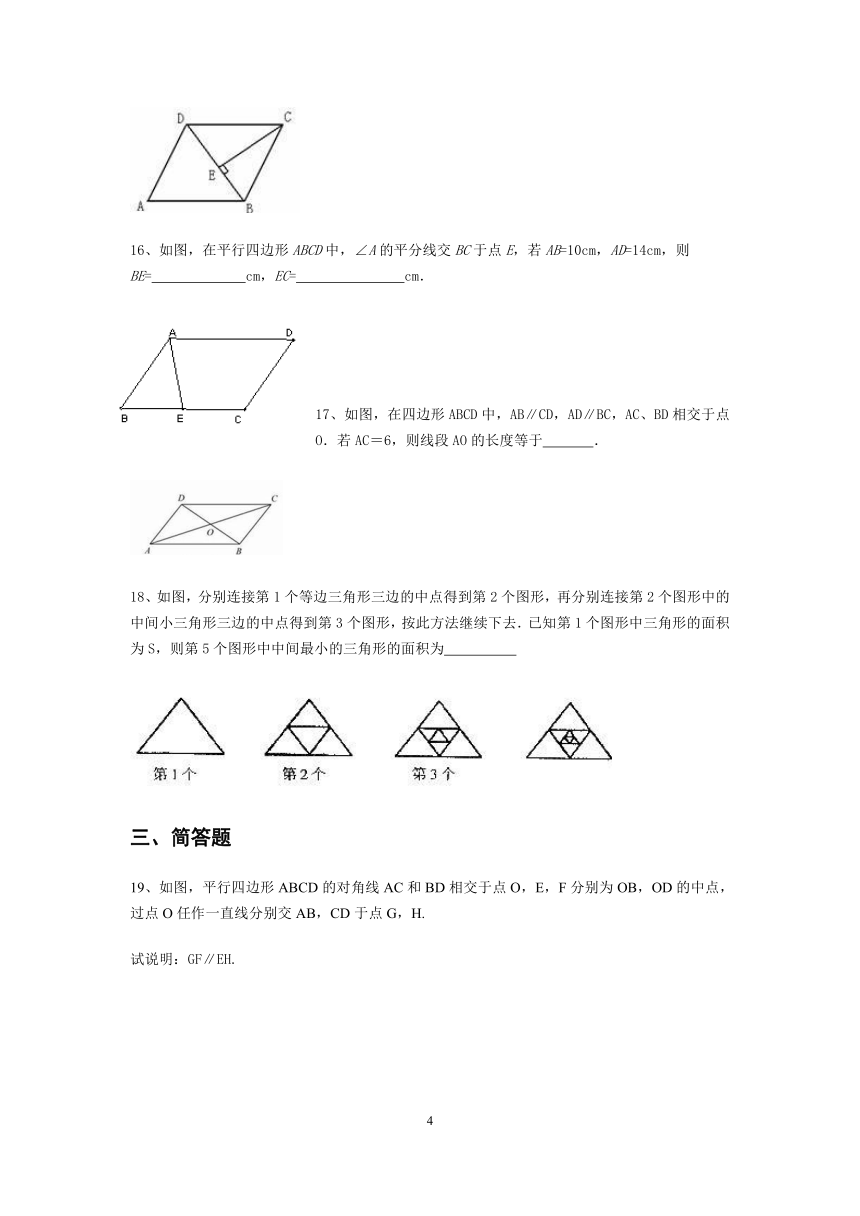
16、如图,在平行四边形ABCD中,∠A的平分线交BC于点E,若AB=10cm,AD=14cm,则BE=??????
cm,EC=???????
cm.
17、如图,在四边形ABCD中,AB∥CD,AD∥BC,AC、BD相交于点O.若AC=6,则线段AO的长度等于???
.
18、如图,分别连接第1个等边三角形三边的中点得到第2个图形,再分别连接第2个图形中的中间小三角形三边的中点得到第3个图形,按此方法继续下去.已知第1个图形中三角形的面积为S,则第5个图形中中间最小的三角形的面积为???
三、简答题
19、如图,平行四边形ABCD的对角线AC和BD相交于点O,E,F分别为OB,OD的中点,过点O任作一直线分别交AB,CD于点G,H.
试说明:GF∥EH.
20、如图,在四边形ABCD中,AB∥CD,AD⊥CD,∠B=45°,延长CD到点E,使DE=DA,连接AE.
(1)求证:AE=BC;(2)若AB=3,CD=1,求四边形ABCE的面积.
21、如图,在?ABCD中,直线EF∥BD,与CD、CB的延长线分别交于点E、F,交AB、AD于G、H.
(1)求证:四边形FBDH为平行四边形;(2)求证:FG=EH.
22、如图,平行四边形ABCD中,BD⊥AD,∠A=45°,E,F分别是AB,CD上的点,且BE=DF,连接EF交BD于点O.
(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于点G,当FG=1时,求AE的长.
23、嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图1的四边形ABCD,并写出了如下不完整的已知和求证.?
(1)已知:如图1,在四边形ABCD中,BC=AD,AB=________?
求证:四边形ABCD是________四边形.
填空,补全已知和求证;
(2)按嘉淇的想法写出证明;???
(3)用文字叙述所证命题的逆命题为________.?
24、已知在□ABCD中,AE?BC于E,DF平分?ADC
交线段AE于F.
(1)如图1,若AE=AD,?ADC=60?,
请直接写出线段CD与AF+BE之间所满足的等量关系;
(2)如图2,
若AE=AD,你在(1)中得到的结论是否仍然成立,
若成立,对你的结论加以证明,
若不成立,
请说明理由;
??
???
????
图1???????????????????
图2????
参考答案
一、选择题
B
;2、A;3、C;4、B;5、C.;6、C
;7、C;8、B;10、B;11、B;12、C;
二、填空题
13、
14、?500,1300
15、
16、.??
BE=10
cm,EC=4cm??
17、3
18、
三、简答题
19、证明:连结EG,FH,由□ABCD得
OA=OC,OB=OD,
又OE=OB,OF=OD,
∴OE=OF,
再证△AOG≌△COH得OG=OH,
∴四边形EHFG是平行四边形,
∴GF∥EH.
20、证明:(1)∵AB∥CD,∠B=45°
∴∠C+∠B=180°
∴∠C=135°
∵DE=DA,AD⊥CD
∴∠E=45°
∵∠E+∠C=180°
∴AE∥BC,且AB∥CD
∴四边形ABCE是平行四边形
∴AE=BC
(2)∵四边形ABCE是平行四边形
∴AB=CE=3
∴AD=DE=AB﹣CD=2
∴四边形ABCE的面积=3×2=6
21、(1)∵四边形ABCD是平行四边形,
∴AD∥BC,∵EF∥BD,
∴四边形FBDH为平行四边形;
(2)∵四边形FBDH为平行四边形,
∴FH=BD,
∵EF∥BD,AB∥DC,
∴四边形BDEG是平行四边形,
∴BD=EG,
∴FH=EG,
∴FH﹣GH=EG﹣GH,
∴FG=EH.
22、解:(1)证明:∵四边形ABCD是平行四边形,∴DC∥AB,∴∠OBE=∠ODF.又∵∠BOE=∠DOF,BE=DF,∴△OBE≌△ODF,∴BO=DO.
(2)∵EF⊥AB,AB∥DC,∴∠GEA=∠GFD=90°.∵∠A=45°,∴∠G=∠A=45°,∴AE=EG.∵BD⊥AD,∴∠ADB=∠GDO=90°,∠GOD=∠G=45°,∴DG=DO,∴OF=FG=1.由(1)可知OE=OF=1,∴GE=OE+OF+FG=3,∴AE=3.
23、(1)CD;平行
(2)证明:连接BD,?
在△ABD和△CDB中,
,
∴△ABD≌△CDB(SSS),
∴∠ADB=∠DBC,∠ABD=∠CDB,
∴AB∥CD,AD∥CB,
∴四边形ABCD是平行四边形
(3)平行四边形两组对边分别相等?
24、(1)CD=AF+BE.
(2)解:(1)中的结论仍然成立.
证明:延长EA到G,使得AG=BE,连结DG.
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,AD=BC.
∵AE⊥BC于点E,
∴∠AEB=∠AEC=90?.
∴∠AEB=∠DAG=90?.
∴∠DAG=90?.
∵AE=AD,
∴△ABE≌△DAG.
∴∠1=∠2,DG=AB.
∴∠GFD=90?-∠3.
∵DF平分∠ADC,
∴∠3=∠4.
∴∠GDF=∠2+∠3=∠1+∠4=180?-∠FAD-∠3=90?-∠3.
∴∠GDF=∠GFD.∴DG=GF.
∴CD=GF=AF+AG=AF+BE.
即CD=AF+BE.
同步练习
选择题
1、下列特征中,平行四边形不一定具有的是(
)
A.邻角互补?????
B.对角互补?????
C.对角相等??????
D.内角和为360°
2、四边形ABCD中,对角线AC与BD交于点O,下列条件中不一定能判定这个四边形是平行四边形的是( )
A.AB∥DC,AD=BC?
B.AD∥BC,AB∥DC
C.AB=DC,AD=BC???
D.OA=OC,OB=OD
3、下列条件中能判定四边形ABCD是平行四边形的是( )
A.∠A=∠B,∠C=∠D
B.AB=AD,CB=CD
C.AB=CD,AD=BC
D.AB∥CD,AD=BC
4、如图,在平行四边形ABCD中,AB=4,BC=6,AC的垂直平分线交AD于点E,则△CDE的周长是( )
A.7??????
B.10????
C.11????
D.12
5、如图,?ABCD中,E,F是对角线BD上的两点,如果添加一个条件,使△ABE≌△CDF,则添加的条件不能为( )
A.BE=DF B.BF=DE C.AE=CF D.∠1=∠2
6、在平面直角坐标系中,□ABCD的顶点A(0,0),B(5,0),D(2,
3),则顶点C的坐标是(?????
)
A、(3,7)????
B、(5,3)?????
C、(7,3)????
D、(8,2)
7、如图,在?ABCD中,E、F、G、H分别是各边的中点,在下列四个图形中,阴影部分的面积与其他三个阴影部分面积不相等的是( )
A.??
B.?
C.
D.
8、如图,在平行四边形ABCD中,过点C的直线CE⊥AB,垂足为E,若∠EAD=53°,则∠BCE的度数为(????
)
A.53°??
B.37°???
C.47°??
D.123°
9、平行四边形的周长为240,两邻边长为x、y,则y与x之间的关系是(????
)
A.y=120﹣x(0<x<120)???
B.y=120﹣x(0≤x≤120)
C.y=240﹣x(0<x<240)???
D.y=240﹣x(0≤x≤240)
10、平行四边形ABCD的周长为2a,两条对角线相交于O,△AOB的周长比△BOC的周长大b,则AB的长为( )
A.???
B.
C.??
?
D.
11、.如图:在?ABCD中,AE⊥BC于E,AF⊥CD于F.若AE=4,AF=6,且?ABCD的周长为30,则ABCD的面积为( )
A.24??
B.36??
C.40??
D.48
12、如图,平行四边形ABCD中,AE平分∠BAD,交BC于点E,且AB=AE,延长AB与DE的延长线交于点F.下列结论中:
①△ABC≌△EAD;②△ABE是等边三角形;③AD=AF;④S△ABE=S△CDE;⑤S△ABE=S△CEF.
其中正确的是( )
A.①②③????
B.①②④????
C.①②⑤????
D.①③④
二、填空题
13、如图,平行四边形ABCD中,、分别为、边上的点,要使需添加一个条件:?????????
.
14、在平行四边形ABCD中,∠A+∠C=100°,则∠A=???
,∠B=???
?.
15、如图,在平行四边形ABCD中,DB=DC、,CEBD于E,则???????
16、如图,在平行四边形ABCD中,∠A的平分线交BC于点E,若AB=10cm,AD=14cm,则BE=??????
cm,EC=???????
cm.
17、如图,在四边形ABCD中,AB∥CD,AD∥BC,AC、BD相交于点O.若AC=6,则线段AO的长度等于???
.
18、如图,分别连接第1个等边三角形三边的中点得到第2个图形,再分别连接第2个图形中的中间小三角形三边的中点得到第3个图形,按此方法继续下去.已知第1个图形中三角形的面积为S,则第5个图形中中间最小的三角形的面积为???
三、简答题
19、如图,平行四边形ABCD的对角线AC和BD相交于点O,E,F分别为OB,OD的中点,过点O任作一直线分别交AB,CD于点G,H.
试说明:GF∥EH.
20、如图,在四边形ABCD中,AB∥CD,AD⊥CD,∠B=45°,延长CD到点E,使DE=DA,连接AE.
(1)求证:AE=BC;(2)若AB=3,CD=1,求四边形ABCE的面积.
21、如图,在?ABCD中,直线EF∥BD,与CD、CB的延长线分别交于点E、F,交AB、AD于G、H.
(1)求证:四边形FBDH为平行四边形;(2)求证:FG=EH.
22、如图,平行四边形ABCD中,BD⊥AD,∠A=45°,E,F分别是AB,CD上的点,且BE=DF,连接EF交BD于点O.
(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于点G,当FG=1时,求AE的长.
23、嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图1的四边形ABCD,并写出了如下不完整的已知和求证.?
(1)已知:如图1,在四边形ABCD中,BC=AD,AB=________?
求证:四边形ABCD是________四边形.
填空,补全已知和求证;
(2)按嘉淇的想法写出证明;???
(3)用文字叙述所证命题的逆命题为________.?
24、已知在□ABCD中,AE?BC于E,DF平分?ADC
交线段AE于F.
(1)如图1,若AE=AD,?ADC=60?,
请直接写出线段CD与AF+BE之间所满足的等量关系;
(2)如图2,
若AE=AD,你在(1)中得到的结论是否仍然成立,
若成立,对你的结论加以证明,
若不成立,
请说明理由;
??
???
????
图1???????????????????
图2????
参考答案
一、选择题
B
;2、A;3、C;4、B;5、C.;6、C
;7、C;8、B;10、B;11、B;12、C;
二、填空题
13、
14、?500,1300
15、
16、.??
BE=10
cm,EC=4cm??
17、3
18、
三、简答题
19、证明:连结EG,FH,由□ABCD得
OA=OC,OB=OD,
又OE=OB,OF=OD,
∴OE=OF,
再证△AOG≌△COH得OG=OH,
∴四边形EHFG是平行四边形,
∴GF∥EH.
20、证明:(1)∵AB∥CD,∠B=45°
∴∠C+∠B=180°
∴∠C=135°
∵DE=DA,AD⊥CD
∴∠E=45°
∵∠E+∠C=180°
∴AE∥BC,且AB∥CD
∴四边形ABCE是平行四边形
∴AE=BC
(2)∵四边形ABCE是平行四边形
∴AB=CE=3
∴AD=DE=AB﹣CD=2
∴四边形ABCE的面积=3×2=6
21、(1)∵四边形ABCD是平行四边形,
∴AD∥BC,∵EF∥BD,
∴四边形FBDH为平行四边形;
(2)∵四边形FBDH为平行四边形,
∴FH=BD,
∵EF∥BD,AB∥DC,
∴四边形BDEG是平行四边形,
∴BD=EG,
∴FH=EG,
∴FH﹣GH=EG﹣GH,
∴FG=EH.
22、解:(1)证明:∵四边形ABCD是平行四边形,∴DC∥AB,∴∠OBE=∠ODF.又∵∠BOE=∠DOF,BE=DF,∴△OBE≌△ODF,∴BO=DO.
(2)∵EF⊥AB,AB∥DC,∴∠GEA=∠GFD=90°.∵∠A=45°,∴∠G=∠A=45°,∴AE=EG.∵BD⊥AD,∴∠ADB=∠GDO=90°,∠GOD=∠G=45°,∴DG=DO,∴OF=FG=1.由(1)可知OE=OF=1,∴GE=OE+OF+FG=3,∴AE=3.
23、(1)CD;平行
(2)证明:连接BD,?
在△ABD和△CDB中,
,
∴△ABD≌△CDB(SSS),
∴∠ADB=∠DBC,∠ABD=∠CDB,
∴AB∥CD,AD∥CB,
∴四边形ABCD是平行四边形
(3)平行四边形两组对边分别相等?
24、(1)CD=AF+BE.
(2)解:(1)中的结论仍然成立.
证明:延长EA到G,使得AG=BE,连结DG.
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,AD=BC.
∵AE⊥BC于点E,
∴∠AEB=∠AEC=90?.
∴∠AEB=∠DAG=90?.
∴∠DAG=90?.
∵AE=AD,
∴△ABE≌△DAG.
∴∠1=∠2,DG=AB.
∴∠GFD=90?-∠3.
∵DF平分∠ADC,
∴∠3=∠4.
∴∠GDF=∠2+∠3=∠1+∠4=180?-∠FAD-∠3=90?-∠3.
∴∠GDF=∠GFD.∴DG=GF.
∴CD=GF=AF+AG=AF+BE.
即CD=AF+BE.
