人教版数学九年级上册:21.2.4 一元二次方程的根与系数的关系 课件(共23张PPT)
文档属性
| 名称 | 人教版数学九年级上册:21.2.4 一元二次方程的根与系数的关系 课件(共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 343.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-19 07:46:56 | ||
图片预览






文档简介
(共23张PPT)
21.2
解一元二次方程
21.2.4
一元二次方程的根与系数的关系
人教版数学九年级上册
1.探索一元二次方程的根与系数的关系.
2.不解方程利用一元二次方程的根与系数的关系解决问题.
3.让学生体会从特殊到一般的科学探究过程.
学习目标
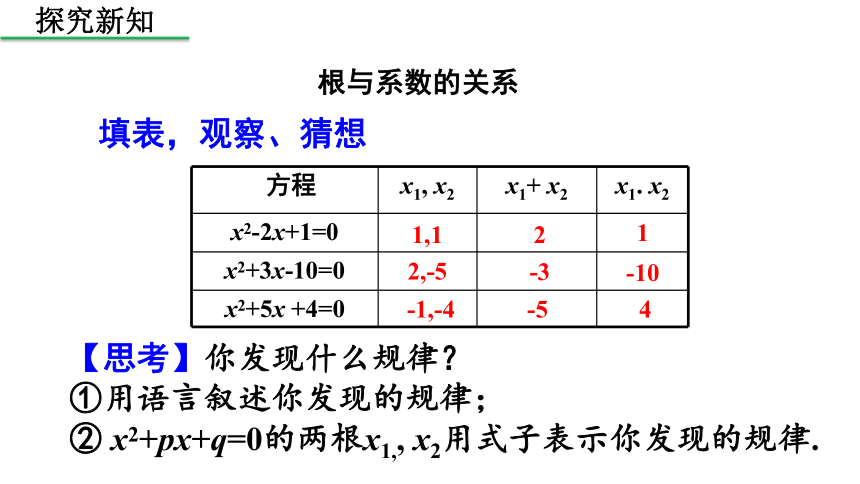
填表,观察、猜想
方程
x1,
x2
x1+
x2
x1.
x2
x2-2x+1=0
x2+3x-10=0
x2+5x
+4=0
【思考】你发现什么规律?
①用语言叙述你发现的规律;
②
x2+px+q=0的两根x1,,
x2用式子表示你发现的规律.
根与系数的关系
1,1
2
1
2,-5
-3
-10
-1,-4
-5
4
探究新知
(1)若一元二次方程的两根为x1,x2,则有x-x1=0,且x-x2=0,那么方程(x-x1)(x-x2)=0(x1,x2为已知数)的两根是什么?将方程化为x2+px+q=0的形式,你能看出x1,x2与p,q之间的关系吗?
(x-x1)(x-x2)=0.
x2-(x1+x2)x+x1·x2=0,
x2+px+q=0,
x1+x2=
-p
,
x1
·x2=q.
【猜一猜】
如果关于x的方程
的两根是x1
,
x2
,则:
如果方程二次项系数不为1呢?
x1+x2=-p,x1·x2=q
方
程
x1,
x2
x1+
x2
x1
.x2
2x2-3x-2=0
3x2-4x+1=0
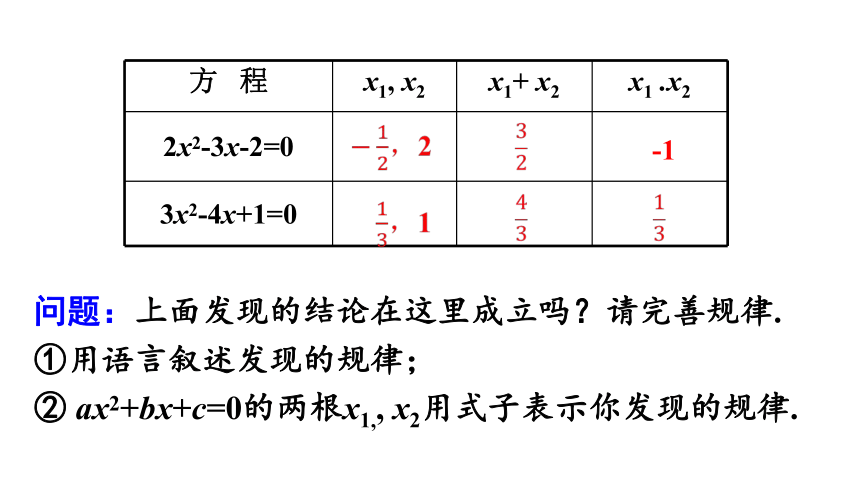
问题:上面发现的结论在这里成立吗?请完善规律.
①用语言叙述发现的规律;
②
ax2+bx+c=0的两根x1,,
x2用式子表示你发现的规律.
?
?
?
?
?
-1
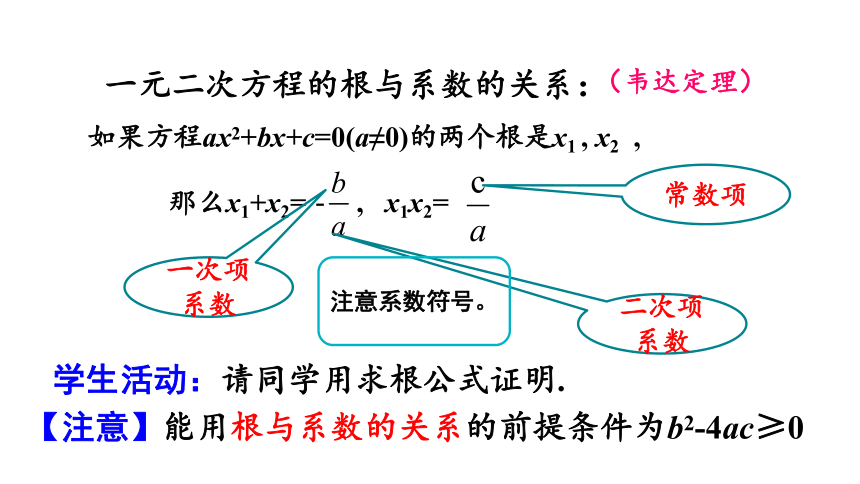
一元二次方程的根与系数的关系:
如果方程ax2+bx+c=0(a≠0)的两个根是x1
,
x2
,
那么x1+x2=
,
x1x2=
(韦达定理)
【注意】能用根与系数的关系的前提条件为b2-4ac≥0
常数项
一次项系数
二次项系数
注意系数符号。
学生活动:请同学用求根公式证明.
考点探究1
一元二次方程的根与系数的关系的应用
例1
利用根与系数的关系,求下列方程的两根之和、两根之积.
(1)x2
+
7x
+
6
=
0;
解:这里
a
=
1
,
b
=
7
,
c
=
6.
Δ
=
b2
-
4ac
=
72
–
4
×
1
×
6
=
25
>
0.
∴方程有两个实数根.
设方程的两个实数根是
x1,
x2,
那么
x1
+
x2
=
-7
,
x1
x2
=
6.
探究新知
(2)2x2
-
3x
-
2
=
0.
解:这里
a
=
2
,
b
=
-3
,
c
=
-2.
Δ=
b2
-
4ac
=
(-
3)2
–
4
×
2
×
(-2)
=
25
>
0,
∴方程有两个实数根.
设方程的两个实数根是
x1,
x2,
那么
x1
+
x2
=
,
x1
x2
=
-1
.
不解方程,求方程两根的和与两根的积:
①x2+3x-1=0
②
2x2-4x+1=0
解:①
②
原方程可化为:
二次项不是1,可以先把它化为1
1.
巩固练习
例2
已知方程5x2+kx-6=0的一个根是2,求它的另一个根及k的值.
解:设方程的两个根分别是x1、x2,其中x1=2
.
所以:x1
·
x2=2x2=
即:x2=
由于x1+x2=2+
=
得:k=-7.
答:方程的另一个根是
,k=-7.
考点探究2
利用根与系数的关系求字母的值或取值范围
想一想,还有没有别的做法?
探究新知
2.
已知方程x2-(k+1)x+3k=0的一个根是2
,求它的另一个根及k的值.
解:
设方程的另一个根为x1.
把x=2代入方程,得
4-2(k+1)+3k=0
解这方程,得
k=
-
2
由根与系数关系,得x1●
2=3k
即
2
x1
=-6
∴
x1
=-3
答:方程的另一个根是-3
,
k的值是-2.
巩固练习
例3
不解方程,求方程2x2+3x-1=0的两根的平方和、倒数和.
解:根据根与系数的关系可知:
考点探究3
利用根与系数的关系求两根的平方和、倒数和
探究新知
(1)x1+x2=
,
(2)
x1·x2=
,
(3)
,
(4)
.
4
1
12
14
3.
设x1,
x2为方程x2-4x+1=0的两个根,则:
巩固练习
例4
设x1,x2是方程
x2
-2(k
-
1)x
+
k2
=0
的两个实数根,且
x12
+x22
=4,求k的值.
解:由方程有两个实数根,得Δ=
4(k
-
1)2
-
4k2
≥
0
即
-8k
+
4
≥
0.
由根与系数的关系得
x1
+
x2
=
2(k
-1)
,
x1
x2
=k
2.
∴
x12
+
x22
=
(x1
+
x2)2
-
2x1x2
=
4(k
-1)2
-2k2
=
2k2
-8k
+
4.
由
x12
+
x22
=
4,得
2k2
-
8k
+
4
=
4,
解得
k1=
0
,
k2
=
4
.
经检验,
k2
=
4
不合题意,舍去.
考点探究4
根与系数关系的综合题目
探究新知
求与方程的根有关的代数式的值时,一般先将所求的代数式化成含两根之和,两根之积的形式,再整体代入.
归纳新知
解:设方程两根分别为x1,x2(x1>x2),则x1-x2=1
∵
(x2-x1)2=(x1+x2)2-4x1x2
由根与系数的关系得x1+x2=
,
x1x2=
解得k1=9,k2=
-3
当k=9或-3时,由于△>0,∴k的值为9或-3.
∴(
)2-4×
=1
4.
当k为何值时,方程2x2-(k+1)x+k+3=0的两根差为1.
巩固练习
1.
如果-1是方程2x2-x+m=0的一个根,则另一个根是___,m
=____.
2.
已知一元二次方程x2+px+q=0的两根分别为-2
和
1
,则:p
=
,
q=
.
1
-2
-3
课堂检测
基础题
3.已知方程
3x2
-19x
+
m=0的一个根是1,求它的另一个根及m的值.
解:将x
=
1代入方程中:
3
-19
+
m
=
0.
解得
m
=
16,
设另一个根为x1,则:
1
×
x1
=
∴x1
=
4.已知x1,x2是方程2x2+2kx+k-1=0的两个根,且(x1+1)(x2+1)=4;
(1)求k的值;
(2)求(x1-x2)2的值.
解:(1)根据根与系数的关系
所以(x1+1)(x2+1)=x1x2+(x1+x2)+1=
解得:k=-7;
(2)因为k=-7,所以
则:
设x1,x2是方程3x2
+
4x
–
3
=
0的两个根.利用根系数之间的关系,求下列各式的值.
(1)
(x1
+
1)(x2
+
1);
(2)
解:
根据根与系数的关系得:
(1)(x1
+
1)(x2
+
1)
=
x1
x2
+
x1
+
x2
+
1=
(2)
提升题
1.
当k为何值时,方程2x2-kx+1=0的两根差为1.
解:设方程两根分别为x1,x2(x1>x2),则x1-x2=1
∵
(x1-x2)2=(x1+x2)2-4x1x2=1
由根与系数的关系,得
∵△>0
拓展题
2.
已知关于x的一元二次方程mx2-2mx+
m
-2=0
(1)若方程有实数根,求实数m的取值范围.
(2)若方程两根x1,x2满足∣x1-x2∣=
1
求m的值.
解:(1)方程有实数根
∴m的取值范围为m>0.
(2)∵方程有实数根x1,x2
∵
(x1-x2)2=(x1+x2)2-4x1x2=1
解得m=8.
经检验m=8是原方程的解.
21.2
解一元二次方程
21.2.4
一元二次方程的根与系数的关系
人教版数学九年级上册
1.探索一元二次方程的根与系数的关系.
2.不解方程利用一元二次方程的根与系数的关系解决问题.
3.让学生体会从特殊到一般的科学探究过程.
学习目标
填表,观察、猜想
方程
x1,
x2
x1+
x2
x1.
x2
x2-2x+1=0
x2+3x-10=0
x2+5x
+4=0
【思考】你发现什么规律?
①用语言叙述你发现的规律;
②
x2+px+q=0的两根x1,,
x2用式子表示你发现的规律.
根与系数的关系
1,1
2
1
2,-5
-3
-10
-1,-4
-5
4
探究新知
(1)若一元二次方程的两根为x1,x2,则有x-x1=0,且x-x2=0,那么方程(x-x1)(x-x2)=0(x1,x2为已知数)的两根是什么?将方程化为x2+px+q=0的形式,你能看出x1,x2与p,q之间的关系吗?
(x-x1)(x-x2)=0.
x2-(x1+x2)x+x1·x2=0,
x2+px+q=0,
x1+x2=
-p
,
x1
·x2=q.
【猜一猜】
如果关于x的方程
的两根是x1
,
x2
,则:
如果方程二次项系数不为1呢?
x1+x2=-p,x1·x2=q
方
程
x1,
x2
x1+
x2
x1
.x2
2x2-3x-2=0
3x2-4x+1=0
问题:上面发现的结论在这里成立吗?请完善规律.
①用语言叙述发现的规律;
②
ax2+bx+c=0的两根x1,,
x2用式子表示你发现的规律.
?
?
?
?
?
-1
一元二次方程的根与系数的关系:
如果方程ax2+bx+c=0(a≠0)的两个根是x1
,
x2
,
那么x1+x2=
,
x1x2=
(韦达定理)
【注意】能用根与系数的关系的前提条件为b2-4ac≥0
常数项
一次项系数
二次项系数
注意系数符号。
学生活动:请同学用求根公式证明.
考点探究1
一元二次方程的根与系数的关系的应用
例1
利用根与系数的关系,求下列方程的两根之和、两根之积.
(1)x2
+
7x
+
6
=
0;
解:这里
a
=
1
,
b
=
7
,
c
=
6.
Δ
=
b2
-
4ac
=
72
–
4
×
1
×
6
=
25
>
0.
∴方程有两个实数根.
设方程的两个实数根是
x1,
x2,
那么
x1
+
x2
=
-7
,
x1
x2
=
6.
探究新知
(2)2x2
-
3x
-
2
=
0.
解:这里
a
=
2
,
b
=
-3
,
c
=
-2.
Δ=
b2
-
4ac
=
(-
3)2
–
4
×
2
×
(-2)
=
25
>
0,
∴方程有两个实数根.
设方程的两个实数根是
x1,
x2,
那么
x1
+
x2
=
,
x1
x2
=
-1
.
不解方程,求方程两根的和与两根的积:
①x2+3x-1=0
②
2x2-4x+1=0
解:①
②
原方程可化为:
二次项不是1,可以先把它化为1
1.
巩固练习
例2
已知方程5x2+kx-6=0的一个根是2,求它的另一个根及k的值.
解:设方程的两个根分别是x1、x2,其中x1=2
.
所以:x1
·
x2=2x2=
即:x2=
由于x1+x2=2+
=
得:k=-7.
答:方程的另一个根是
,k=-7.
考点探究2
利用根与系数的关系求字母的值或取值范围
想一想,还有没有别的做法?
探究新知
2.
已知方程x2-(k+1)x+3k=0的一个根是2
,求它的另一个根及k的值.
解:
设方程的另一个根为x1.
把x=2代入方程,得
4-2(k+1)+3k=0
解这方程,得
k=
-
2
由根与系数关系,得x1●
2=3k
即
2
x1
=-6
∴
x1
=-3
答:方程的另一个根是-3
,
k的值是-2.
巩固练习
例3
不解方程,求方程2x2+3x-1=0的两根的平方和、倒数和.
解:根据根与系数的关系可知:
考点探究3
利用根与系数的关系求两根的平方和、倒数和
探究新知
(1)x1+x2=
,
(2)
x1·x2=
,
(3)
,
(4)
.
4
1
12
14
3.
设x1,
x2为方程x2-4x+1=0的两个根,则:
巩固练习
例4
设x1,x2是方程
x2
-2(k
-
1)x
+
k2
=0
的两个实数根,且
x12
+x22
=4,求k的值.
解:由方程有两个实数根,得Δ=
4(k
-
1)2
-
4k2
≥
0
即
-8k
+
4
≥
0.
由根与系数的关系得
x1
+
x2
=
2(k
-1)
,
x1
x2
=k
2.
∴
x12
+
x22
=
(x1
+
x2)2
-
2x1x2
=
4(k
-1)2
-2k2
=
2k2
-8k
+
4.
由
x12
+
x22
=
4,得
2k2
-
8k
+
4
=
4,
解得
k1=
0
,
k2
=
4
.
经检验,
k2
=
4
不合题意,舍去.
考点探究4
根与系数关系的综合题目
探究新知
求与方程的根有关的代数式的值时,一般先将所求的代数式化成含两根之和,两根之积的形式,再整体代入.
归纳新知
解:设方程两根分别为x1,x2(x1>x2),则x1-x2=1
∵
(x2-x1)2=(x1+x2)2-4x1x2
由根与系数的关系得x1+x2=
,
x1x2=
解得k1=9,k2=
-3
当k=9或-3时,由于△>0,∴k的值为9或-3.
∴(
)2-4×
=1
4.
当k为何值时,方程2x2-(k+1)x+k+3=0的两根差为1.
巩固练习
1.
如果-1是方程2x2-x+m=0的一个根,则另一个根是___,m
=____.
2.
已知一元二次方程x2+px+q=0的两根分别为-2
和
1
,则:p
=
,
q=
.
1
-2
-3
课堂检测
基础题
3.已知方程
3x2
-19x
+
m=0的一个根是1,求它的另一个根及m的值.
解:将x
=
1代入方程中:
3
-19
+
m
=
0.
解得
m
=
16,
设另一个根为x1,则:
1
×
x1
=
∴x1
=
4.已知x1,x2是方程2x2+2kx+k-1=0的两个根,且(x1+1)(x2+1)=4;
(1)求k的值;
(2)求(x1-x2)2的值.
解:(1)根据根与系数的关系
所以(x1+1)(x2+1)=x1x2+(x1+x2)+1=
解得:k=-7;
(2)因为k=-7,所以
则:
设x1,x2是方程3x2
+
4x
–
3
=
0的两个根.利用根系数之间的关系,求下列各式的值.
(1)
(x1
+
1)(x2
+
1);
(2)
解:
根据根与系数的关系得:
(1)(x1
+
1)(x2
+
1)
=
x1
x2
+
x1
+
x2
+
1=
(2)
提升题
1.
当k为何值时,方程2x2-kx+1=0的两根差为1.
解:设方程两根分别为x1,x2(x1>x2),则x1-x2=1
∵
(x1-x2)2=(x1+x2)2-4x1x2=1
由根与系数的关系,得
∵△>0
拓展题
2.
已知关于x的一元二次方程mx2-2mx+
m
-2=0
(1)若方程有实数根,求实数m的取值范围.
(2)若方程两根x1,x2满足∣x1-x2∣=
1
求m的值.
解:(1)方程有实数根
∴m的取值范围为m>0.
(2)∵方程有实数根x1,x2
∵
(x1-x2)2=(x1+x2)2-4x1x2=1
解得m=8.
经检验m=8是原方程的解.
同课章节目录
