北师大版八年级数学下册 第5章 分式与分式方程达标测评卷(含答案)
文档属性
| 名称 | 北师大版八年级数学下册 第5章 分式与分式方程达标测评卷(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 106.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-18 00:00:00 | ||
图片预览




文档简介
北师大版八年级数学下册
第5章
达标测评卷
(满分:120分,时间:90分钟)
题 号
一
二
三
总 分
得 分
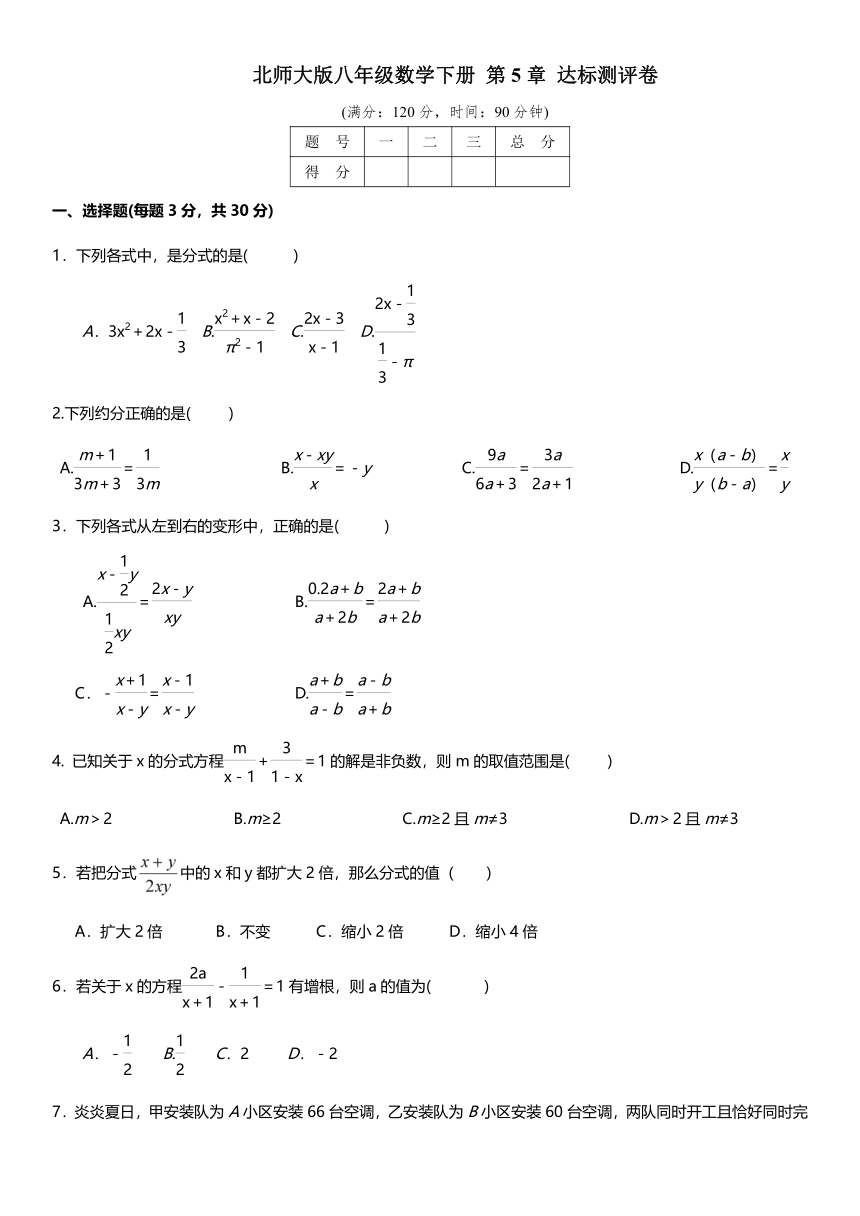
一、选择题(每题3分,共30分)
1.下列各式中,是分式的是(
)
A.3x2+2x-
B.
C.
D.
2.下列约分正确的是(
)
A.=
B.=-y
C.=
D.=
3.下列各式从左到右的变形中,正确的是(
)
A.=
B.=
C.-=
D.=
4.
已知关于x的分式方程+=1的解是非负数,则m的取值范围是(
)
A.m>2
B.m≥2
C.m≥2且m≠3
D.m>2且m≠3
5.若把分式中的x和y都扩大2倍,那么分式的值(
)
A.扩大2倍
B.不变
C.缩小2倍
D.缩小4倍
6.若关于x的方程-=1有增根,则a的值为(
)
A.-
B.
C.2
D.-2
7.炎炎夏日,甲安装队为A小区安装66台空调,乙安装队为B小区安装60台空调,两队同时开工且恰好同时完工,甲队比乙队每天多安装2台.设乙队每天安装x台,根据题意下面所列方程正确的是(
)
A.=
B.=
C.=
D.=
8.已知,且,则的值为(
)
A.
B.
C.2
D.
9.已知a2-3a+1=0,则分式的值是(
)
A.3
B.
C.7
D.
10.已知甲做360个零件与乙做480个零件所用的时间相同,两人每天共做140个零件,设甲每天做x个零件,根据题意,可列方程为( B )
A.
B.
C.
D.
二、填空题(每题3分,共30分)
11.纳米(nm)是一种长度单位,常用于度量物质原子的大小,1
nm=10-9
m.已知某种植物孢子的直径为45
000
nm,用科学记数法表示该孢子的直径为____________m.
12.化简÷的结果是________.
13.若代数式和的值相等,则x=________.
14.已知-=,则的值等于________.
15.计算:-=________.
16.当x=________时,2x-3与的值互为倒数.
17.已知a2-6a+9与|b-1|互为相反数,则式子÷(a+b)的值为________.
18.若关于x的分式方程-m=无解,则m的值为________.
19.当前控制通货膨胀、保持物价稳定是政府的头等大事,许多企业积极履行社会责任,在销售中保持价格稳定已成为一种自觉行为.某企业原来的销售利润率是32%.现在由于进价提高了10%,而售价保持不变,所以该企业的销售利润率变成了________.(注:销售利润率=(售价-进价)÷进价)
20.若=+,对任意自然数n都成立,则a=________,b=________;计算:m=+++…+=________.
三、解答题(21题20分,22题8分,23,24题每题6分,其余每题10分,共60分)
21.计算:
(1)+(3.14-π)0+-|-2|;
(2)b2c-2·;
(3)·÷;
(4)÷;
(5)÷.
22.解分式方程:
(1)=-.
(2)1-=.
23.已知y=÷-x+3,试说明:x取任何有意义的值,y值均不变.
24.先化简,再求值:·+,其中x是从-1,0,1,2中选取的一个合适的数.
25.某校组织学生到生态园春游,某班学生9:00从樱花园出发,匀速前往距樱花园2
km的桃花园.在桃花园停留1
h后,按原路返回樱花园,返程中先按原来的速度行走了6
min,随后接到通知,要尽快回到樱花园,故速度提高到原来的2倍,于10:48回到了樱花园,求这班学生原来的行走速度.
26.观察下列等式:
=1-,=-,=-.
将以上三个等式的两边分别相加,得:
++=1-+-+-=1-=.
(1)直接写出计算结果:
+++…+=________.
(2)仿照=1-,=-,=-的形式,猜想并写出:=________.
(3)解方程:++=.
参考答案
一、1.C 2.C 3.A 4.C 5.C 6.A
7.D 8.A
9.D 10.B
二、11.4.5×10-5
12.m
13.7
14.-6
15.
16.3
17. 点拨:利用非负数的性质求出a,b的值,再代入所求式子求值即可.
18.1或± 点拨:本题利用了分类讨论思想.将原方程化为整式方程,得(1-m)x=m2-3m.分两种情况:
(1)当1-m=0时,整式方程无解,解得m=1;
(2)当x=3时,原方程无解,把x=3代入整式方程,解得m=±.综上,得m=1或±.
19.20% 点拨:设原来的售价是b元,进价是a元,由题意得×100%=32%.解得b=1.32a.现在的销售利润率为×100%=20%.
20.;-;
点拨:∵==+,∴a=,b=-.利用上述结论可得:m=×(1-+-+-+…+-)=×=×=.
三、21.解:(1)原式=2+1+4-2=5;
(2)原式=b2c-2·8b6c-6=8b8c-8=;
(3)原式=·(-)·=-x5;
(4)原式=÷
=×
=;
(5)原式=÷
=×
=.
22.解:(1)方程两边同时乘以2(2x-1),得2=2x-1-3.
化简,得2x=6.解得x=3.
检验:当x=3时,2(2x-1)=2(2×3-1)≠0,
所以,x=3是原方程的解.
(2)去分母,得x-3-2=1,
解这个方程,得x=6.
检验:当x=6时,x-3=6-3≠0,
所以x=6是原方程的解.
23.解:y=÷-x+3
=×-x+3=x-x+3=3.
故x取任何有意义的值,y值均不变.
24.解:原式=·+
=+
=+
=.
因为x2-1≠0,且x2-4x+4≠0,且x-1≠0,所以x≠-1,且x≠1,且x≠2,所以x=0.
当x=0时,原式=-.
25.解:设这班学生原来的行走速度为x
km/h.易知从9:00到10:48共1.8
h,
故可列方程为+++1=1.8,解得x=4.
经检验,x=4是原方程的解,且符合题意.
答:这班学生原来的行走速度为4
km/h.
26.解:(1) (2)
(3)仿照(2)中的结论,原方程可变形为
(-+-+-)=,
即=,
解得x=2.
经检验,x=2是原分式方程的解.
第5章
达标测评卷
(满分:120分,时间:90分钟)
题 号
一
二
三
总 分
得 分
一、选择题(每题3分,共30分)
1.下列各式中,是分式的是(
)
A.3x2+2x-
B.
C.
D.
2.下列约分正确的是(
)
A.=
B.=-y
C.=
D.=
3.下列各式从左到右的变形中,正确的是(
)
A.=
B.=
C.-=
D.=
4.
已知关于x的分式方程+=1的解是非负数,则m的取值范围是(
)
A.m>2
B.m≥2
C.m≥2且m≠3
D.m>2且m≠3
5.若把分式中的x和y都扩大2倍,那么分式的值(
)
A.扩大2倍
B.不变
C.缩小2倍
D.缩小4倍
6.若关于x的方程-=1有增根,则a的值为(
)
A.-
B.
C.2
D.-2
7.炎炎夏日,甲安装队为A小区安装66台空调,乙安装队为B小区安装60台空调,两队同时开工且恰好同时完工,甲队比乙队每天多安装2台.设乙队每天安装x台,根据题意下面所列方程正确的是(
)
A.=
B.=
C.=
D.=
8.已知,且,则的值为(
)
A.
B.
C.2
D.
9.已知a2-3a+1=0,则分式的值是(
)
A.3
B.
C.7
D.
10.已知甲做360个零件与乙做480个零件所用的时间相同,两人每天共做140个零件,设甲每天做x个零件,根据题意,可列方程为( B )
A.
B.
C.
D.
二、填空题(每题3分,共30分)
11.纳米(nm)是一种长度单位,常用于度量物质原子的大小,1
nm=10-9
m.已知某种植物孢子的直径为45
000
nm,用科学记数法表示该孢子的直径为____________m.
12.化简÷的结果是________.
13.若代数式和的值相等,则x=________.
14.已知-=,则的值等于________.
15.计算:-=________.
16.当x=________时,2x-3与的值互为倒数.
17.已知a2-6a+9与|b-1|互为相反数,则式子÷(a+b)的值为________.
18.若关于x的分式方程-m=无解,则m的值为________.
19.当前控制通货膨胀、保持物价稳定是政府的头等大事,许多企业积极履行社会责任,在销售中保持价格稳定已成为一种自觉行为.某企业原来的销售利润率是32%.现在由于进价提高了10%,而售价保持不变,所以该企业的销售利润率变成了________.(注:销售利润率=(售价-进价)÷进价)
20.若=+,对任意自然数n都成立,则a=________,b=________;计算:m=+++…+=________.
三、解答题(21题20分,22题8分,23,24题每题6分,其余每题10分,共60分)
21.计算:
(1)+(3.14-π)0+-|-2|;
(2)b2c-2·;
(3)·÷;
(4)÷;
(5)÷.
22.解分式方程:
(1)=-.
(2)1-=.
23.已知y=÷-x+3,试说明:x取任何有意义的值,y值均不变.
24.先化简,再求值:·+,其中x是从-1,0,1,2中选取的一个合适的数.
25.某校组织学生到生态园春游,某班学生9:00从樱花园出发,匀速前往距樱花园2
km的桃花园.在桃花园停留1
h后,按原路返回樱花园,返程中先按原来的速度行走了6
min,随后接到通知,要尽快回到樱花园,故速度提高到原来的2倍,于10:48回到了樱花园,求这班学生原来的行走速度.
26.观察下列等式:
=1-,=-,=-.
将以上三个等式的两边分别相加,得:
++=1-+-+-=1-=.
(1)直接写出计算结果:
+++…+=________.
(2)仿照=1-,=-,=-的形式,猜想并写出:=________.
(3)解方程:++=.
参考答案
一、1.C 2.C 3.A 4.C 5.C 6.A
7.D 8.A
9.D 10.B
二、11.4.5×10-5
12.m
13.7
14.-6
15.
16.3
17. 点拨:利用非负数的性质求出a,b的值,再代入所求式子求值即可.
18.1或± 点拨:本题利用了分类讨论思想.将原方程化为整式方程,得(1-m)x=m2-3m.分两种情况:
(1)当1-m=0时,整式方程无解,解得m=1;
(2)当x=3时,原方程无解,把x=3代入整式方程,解得m=±.综上,得m=1或±.
19.20% 点拨:设原来的售价是b元,进价是a元,由题意得×100%=32%.解得b=1.32a.现在的销售利润率为×100%=20%.
20.;-;
点拨:∵==+,∴a=,b=-.利用上述结论可得:m=×(1-+-+-+…+-)=×=×=.
三、21.解:(1)原式=2+1+4-2=5;
(2)原式=b2c-2·8b6c-6=8b8c-8=;
(3)原式=·(-)·=-x5;
(4)原式=÷
=×
=;
(5)原式=÷
=×
=.
22.解:(1)方程两边同时乘以2(2x-1),得2=2x-1-3.
化简,得2x=6.解得x=3.
检验:当x=3时,2(2x-1)=2(2×3-1)≠0,
所以,x=3是原方程的解.
(2)去分母,得x-3-2=1,
解这个方程,得x=6.
检验:当x=6时,x-3=6-3≠0,
所以x=6是原方程的解.
23.解:y=÷-x+3
=×-x+3=x-x+3=3.
故x取任何有意义的值,y值均不变.
24.解:原式=·+
=+
=+
=.
因为x2-1≠0,且x2-4x+4≠0,且x-1≠0,所以x≠-1,且x≠1,且x≠2,所以x=0.
当x=0时,原式=-.
25.解:设这班学生原来的行走速度为x
km/h.易知从9:00到10:48共1.8
h,
故可列方程为+++1=1.8,解得x=4.
经检验,x=4是原方程的解,且符合题意.
答:这班学生原来的行走速度为4
km/h.
26.解:(1) (2)
(3)仿照(2)中的结论,原方程可变形为
(-+-+-)=,
即=,
解得x=2.
经检验,x=2是原分式方程的解.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
