勾股定理
图片预览





文档简介
(共21张PPT)
课题:18.1 勾股定理(1)
凤阳博文国际学校:郝为祯
a2+b2=c2
a
b
c
左下图是2002年在北京召开的国际数学家大会会徽
毕达哥拉斯
(公元前572----前492年),
古希腊著名的哲学家、数学家、天文学家。
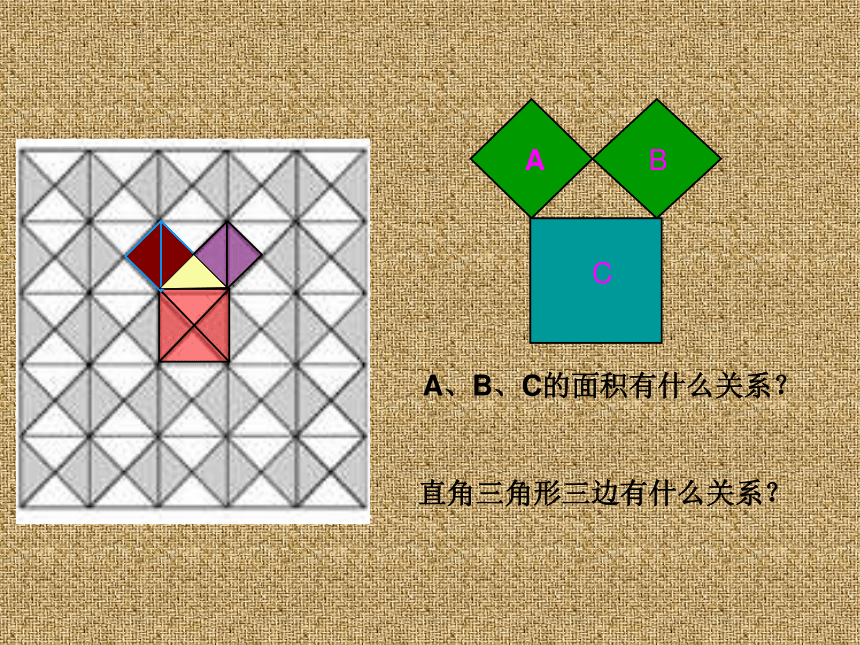
相传在2500年前,毕达哥拉斯有一次在朋友家做客时,发现朋友家用砖铺成的地面中反映了直角三角形三边的某种数量关系,我们一起来观察图中的地面,看看能发现什么。
毕达哥拉斯
(公元前572----前492年),
古希腊著名的哲学家、数学家、天文学家。
相传在2500年前,毕达哥拉斯有一次在朋友家做客时,发现朋友家用砖铺成的地面中反映了直角三角形三边的某种数量关系,我们一起来观察图中的地面,看看能发现什么。
A、B、C的面积有什么关系?
直角三角形三边有什么关系?
A
B
C
A
B
C
A
B
C
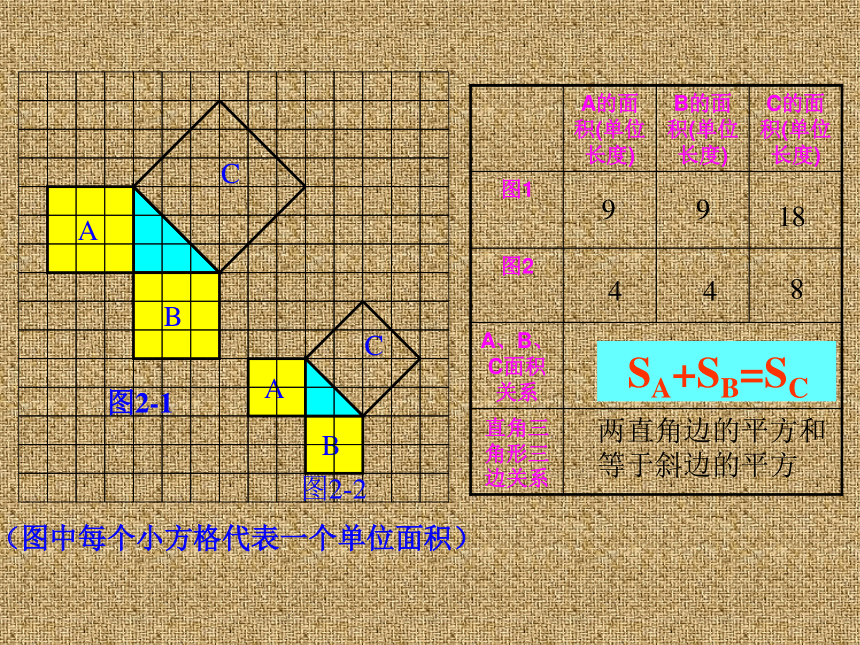
(图中每个小方格代表一个单位面积)
图2-1
图2-2
SA+SB=SC
A的面积(单位长度) B的面积(单位长度) C的面积(单位长度)
图1
图2
A、B、C面积关系
直角三角形三边关系
4
4
8
两直角边的平方和
等于斜边的平方
9
9
18
A
B
C
A
B
C
A的面积(单位长度) B的面积(单位长度) C的面积(单位长度)
图2
图3
A、B、C面积关系
直角三角形三边关系
图2
图3
4
9
13
9
25
34
sA+sB=sC
两直角边的平方和
等于斜边的平方
A
B
C
a
c
b
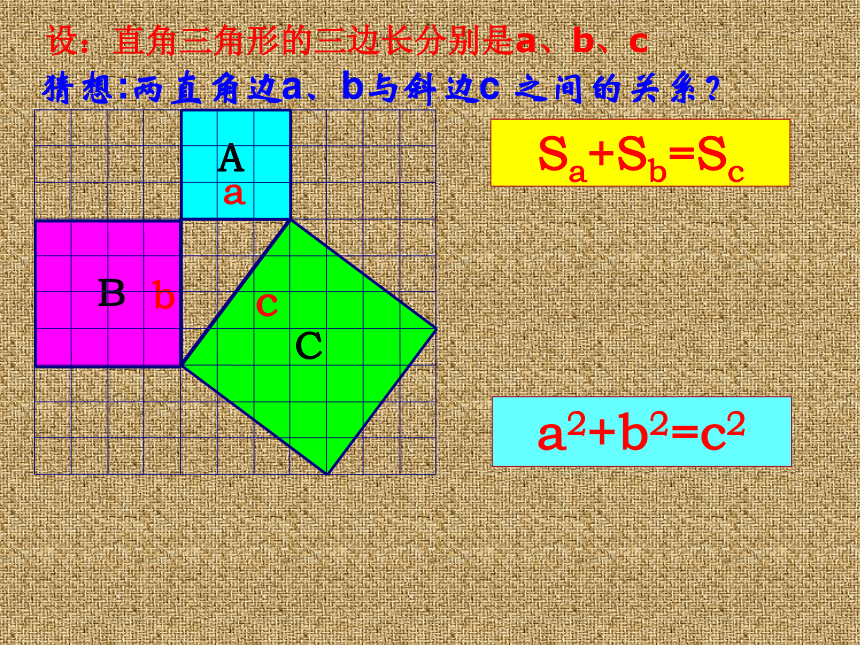
Sa+Sb=Sc
设:直角三角形的三边长分别是a、b、c
猜想:两直角边a、b与斜边c 之间的关系?
a2+b2=c2
┏
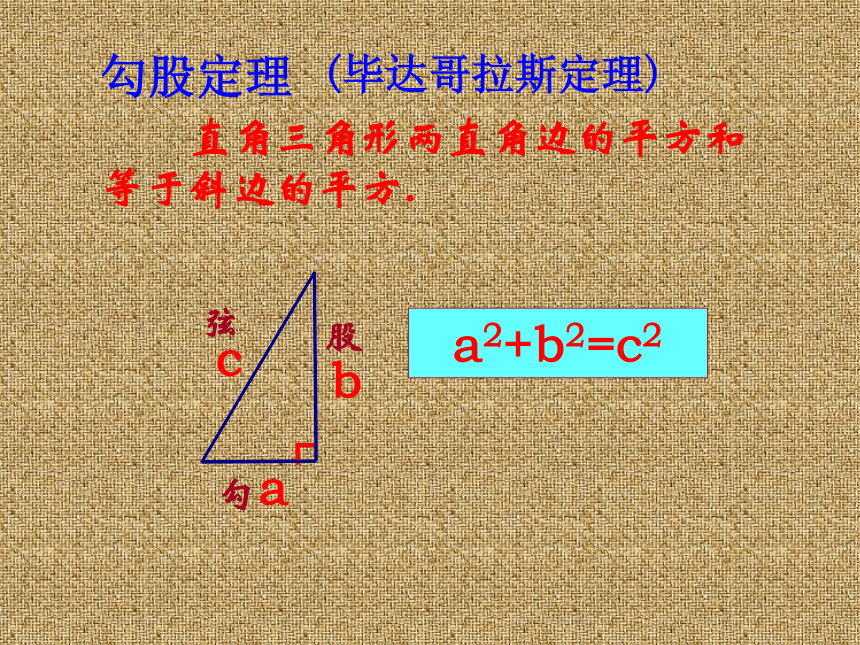
a2+b2=c2
a
c
b
直角三角形两直角边的平方和等于斜边的平方.
勾
股
弦
勾股定理
(毕达哥拉斯定理)
c
b a
c2 = (a b)2 + 4( ab)
= a2 2ab + b2 + 2ab
c2 = a2 + b2
依据科学理论的证实:一
3世纪我国汉代的赵爽指出:四个全等的直角三角形如下拼成一个中空的正方形,由大正方形的面积等于小正方形的面积与4个三角形的面积和得: 两直角边的平方和
等于斜边的平方
赵爽弦图
“赵爽弦图”表现了我国古代人对数学的钻研精神和聪明才智,它是我国数学的骄傲。 中国古代的数学家们不仅很早就发现并应用勾股定理,而且很早就尝试对勾股定理作理论的证明。最早对勾股定理进行证明的,是三国时期吴国的数学家赵爽。正因为此,这个图案被选为2002年在北京召开的国际数学家大会会徽。
操作 请大家将手中的四个全等的直角边长分别为a、b,斜边为c的直角三角形,拼成如图所示的正方形,并找出图中的面积关系。
A
B
C
a
c
b
c
c
c
c
a
b
B1
a
b
C1
F
a
b
D1
G
a
b
A1
E
H
图中的面积关系是:
S正方形EFGH-4S△ABC=S正方形A1B1C1D1
由此,你能得出勾股定理的证明方法吗?
已知:如图,在Rt△ABC中,∠C=90°,AB=c,BC=a,AC=b.求证:a2+b2=c2.
证明 取4个与Rt△ABC全等的直角三角形,把它们拼成如图所示的边长为a+b的正方形EFGH。
可以证明四边形A1B1C1D1是边长为c的正方形(为什么?)。
且 S正方形EFGH-4S△ABC=S正方形A1B1C1D1
即 (a+b)2-4× ab=c2.
化简,得a2+b2=c2.
(a + b)(b + a) = c2 + 2( ab)
a2 + ab + b2 = c2 + ab
a2 + b2 = c2
a
a
b
b
c
c
伽菲尔德经过反复的思考与演算,终于弄清楚了其中的道理,并给出了简洁的证明方法.1876年4月1日,伽菲尔德在《新英格兰教育日志》上发表了他对勾股定理的这一证法。1881年,伽菲尔德就任美国第二十任总统后,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就称这一证法称为“总统”证法。
∟
∟
∟
a
b
c
c2=a2 + b2
如果直角三角形两直角边分别为a,b,斜边为c,那么
a2 + b2 = c2
勾股定理
结论变形
8
15
A
49
B
25
1.求下列图中字母所代表的正方形的面积:
y=0
学以致用,做一做
结论:
S1+S2+S3+S4
=S5+S6
=S7
y=0
学海无涯
y=0
2.求出下列直角三角形中未知边的长度
6
8
x
5
x
13
学以致用,做一做
解:(1)在Rt△ABC中,由勾股定理得:AB2=AC2+BC2
X2 =36+64
x2 =100
x2=62+82
∴ x=10
∵x>0
x2+52=132
x2=132-52
x2=144
∴ x=12
(2)在Rt△ABC中,由勾股定理:AB2+AC2=BC2
∵x>0
A
C
B
A
C
B
3.在一个直角三角形中, 两边长分别为6、
8,则第三边的长为________
10
y=0
练一练
或
★这节课你学会了哪些知识?说说你的收获。
课堂小结
★请说出你的困惑,与你的同伴和老师交流。
“堂堂清”过关检测:
驶向胜利的 彼岸
课题:18.1 勾股定理(1)
凤阳博文国际学校:郝为祯
a2+b2=c2
a
b
c
左下图是2002年在北京召开的国际数学家大会会徽
毕达哥拉斯
(公元前572----前492年),
古希腊著名的哲学家、数学家、天文学家。
相传在2500年前,毕达哥拉斯有一次在朋友家做客时,发现朋友家用砖铺成的地面中反映了直角三角形三边的某种数量关系,我们一起来观察图中的地面,看看能发现什么。
毕达哥拉斯
(公元前572----前492年),
古希腊著名的哲学家、数学家、天文学家。
相传在2500年前,毕达哥拉斯有一次在朋友家做客时,发现朋友家用砖铺成的地面中反映了直角三角形三边的某种数量关系,我们一起来观察图中的地面,看看能发现什么。
A、B、C的面积有什么关系?
直角三角形三边有什么关系?
A
B
C
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图2-1
图2-2
SA+SB=SC
A的面积(单位长度) B的面积(单位长度) C的面积(单位长度)
图1
图2
A、B、C面积关系
直角三角形三边关系
4
4
8
两直角边的平方和
等于斜边的平方
9
9
18
A
B
C
A
B
C
A的面积(单位长度) B的面积(单位长度) C的面积(单位长度)
图2
图3
A、B、C面积关系
直角三角形三边关系
图2
图3
4
9
13
9
25
34
sA+sB=sC
两直角边的平方和
等于斜边的平方
A
B
C
a
c
b
Sa+Sb=Sc
设:直角三角形的三边长分别是a、b、c
猜想:两直角边a、b与斜边c 之间的关系?
a2+b2=c2
┏
a2+b2=c2
a
c
b
直角三角形两直角边的平方和等于斜边的平方.
勾
股
弦
勾股定理
(毕达哥拉斯定理)
c
b a
c2 = (a b)2 + 4( ab)
= a2 2ab + b2 + 2ab
c2 = a2 + b2
依据科学理论的证实:一
3世纪我国汉代的赵爽指出:四个全等的直角三角形如下拼成一个中空的正方形,由大正方形的面积等于小正方形的面积与4个三角形的面积和得: 两直角边的平方和
等于斜边的平方
赵爽弦图
“赵爽弦图”表现了我国古代人对数学的钻研精神和聪明才智,它是我国数学的骄傲。 中国古代的数学家们不仅很早就发现并应用勾股定理,而且很早就尝试对勾股定理作理论的证明。最早对勾股定理进行证明的,是三国时期吴国的数学家赵爽。正因为此,这个图案被选为2002年在北京召开的国际数学家大会会徽。
操作 请大家将手中的四个全等的直角边长分别为a、b,斜边为c的直角三角形,拼成如图所示的正方形,并找出图中的面积关系。
A
B
C
a
c
b
c
c
c
c
a
b
B1
a
b
C1
F
a
b
D1
G
a
b
A1
E
H
图中的面积关系是:
S正方形EFGH-4S△ABC=S正方形A1B1C1D1
由此,你能得出勾股定理的证明方法吗?
已知:如图,在Rt△ABC中,∠C=90°,AB=c,BC=a,AC=b.求证:a2+b2=c2.
证明 取4个与Rt△ABC全等的直角三角形,把它们拼成如图所示的边长为a+b的正方形EFGH。
可以证明四边形A1B1C1D1是边长为c的正方形(为什么?)。
且 S正方形EFGH-4S△ABC=S正方形A1B1C1D1
即 (a+b)2-4× ab=c2.
化简,得a2+b2=c2.
(a + b)(b + a) = c2 + 2( ab)
a2 + ab + b2 = c2 + ab
a2 + b2 = c2
a
a
b
b
c
c
伽菲尔德经过反复的思考与演算,终于弄清楚了其中的道理,并给出了简洁的证明方法.1876年4月1日,伽菲尔德在《新英格兰教育日志》上发表了他对勾股定理的这一证法。1881年,伽菲尔德就任美国第二十任总统后,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就称这一证法称为“总统”证法。
∟
∟
∟
a
b
c
c2=a2 + b2
如果直角三角形两直角边分别为a,b,斜边为c,那么
a2 + b2 = c2
勾股定理
结论变形
8
15
A
49
B
25
1.求下列图中字母所代表的正方形的面积:
y=0
学以致用,做一做
结论:
S1+S2+S3+S4
=S5+S6
=S7
y=0
学海无涯
y=0
2.求出下列直角三角形中未知边的长度
6
8
x
5
x
13
学以致用,做一做
解:(1)在Rt△ABC中,由勾股定理得:AB2=AC2+BC2
X2 =36+64
x2 =100
x2=62+82
∴ x=10
∵x>0
x2+52=132
x2=132-52
x2=144
∴ x=12
(2)在Rt△ABC中,由勾股定理:AB2+AC2=BC2
∵x>0
A
C
B
A
C
B
3.在一个直角三角形中, 两边长分别为6、
8,则第三边的长为________
10
y=0
练一练
或
★这节课你学会了哪些知识?说说你的收获。
课堂小结
★请说出你的困惑,与你的同伴和老师交流。
“堂堂清”过关检测:
驶向胜利的 彼岸
