人教版九年级数学下册 26.2 实际问题与反比例函数(33张ppt)
文档属性
| 名称 | 人教版九年级数学下册 26.2 实际问题与反比例函数(33张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-18 14:46:55 | ||
图片预览











文档简介
(共33张PPT)
反比例函数
26
26.2
实际问题与反比例函数
学习目标
教学分析
1.经历在具体问题中探究反比例函数应用的过程,体会反比例函数作为一种数学模型的意义。
2.利用反比例函数的知识分析和解决实际问题。
3.渗透数形结合思想,提高用函数观点解决问题的能力。
复习回顾
反比例函数的性质
当k>0时,双曲线的两支分别在第一、三象限,
在每一个象限内,y随x的增大而减小;
当k<0时,双曲线的两支分别在第二、四象限,
在每一个象限内,y随x的增大而增大。
复习回顾
双曲线不过原点且与两坐标轴永不相交,但无限靠近x
轴、y
轴。
反比例函数的性质
反比例函数的图象既是中心对称图形,又是轴对称图形;
对称中心是原点,有两条对称轴。
复习回顾
反比例函数与一次函数综合应用
1.
如图,一次函数y1=x-1与反比例函数y2=
的图象交于点A(2,1),
B(-1,-2),则使y1
>y2的x
的取值范围是(
)。
x>2
B.
x>2
或-1<x<0
C.
-1<x<2
D.
x>2
或x<-1
B
复习回顾
2.
如图,已知A(-4,2)、B(n,-4)是一次函数的图象
与反比例函数的图象的两个交点。
(1)求此反比例函数和一次函数的解析式;
一次函数的解析式:
y=-x-2
反比例函数解析式:
复习回顾
(2)
根据图象写出使一次函数的值小于
反比例函数的值的x的取值范围。
x的取值范围为:
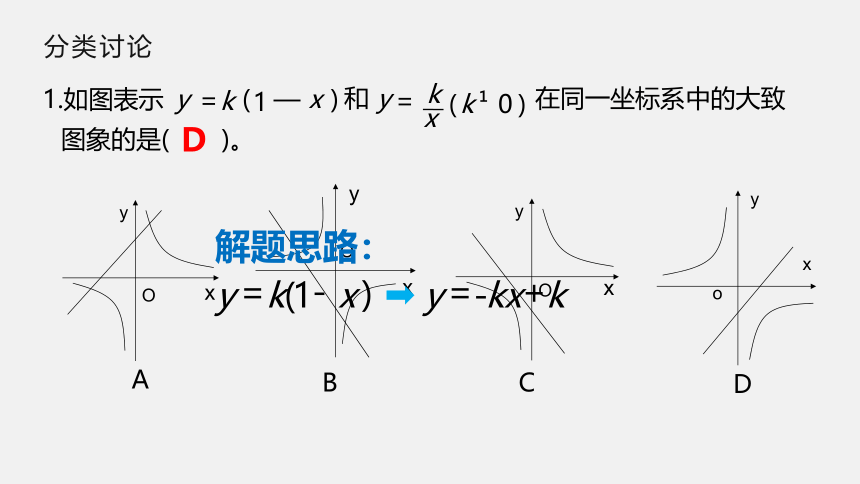
分类讨论
1.如图表示
)
(
—
=
x
k
y
1
和
y
)
0
(
?
=
k
x
k
在同一坐标系中的大致
图象的是(
)。
D
O
x
y
A
C
O
x
y
D
x
y
o
O
x
y
B
解题思路:
k
kx
y
+
=
-
)
x
k
y
-
=
1
(
数形结合
2.
已知点A(2,y1),B(5,y2),C(-3,y3)是反比例函数
图象上的三点。
请比较y1,y2,y3的大小。
x
y
O
2
5
y1
y2
A
B
y3
C
-3
(1)代入求值。
(2)利用增减性。
(3)根据图象判断。
例题讲解
知识点一
用反比例函数解决体积问题
例题讲解
例1
市煤气公司要在地下修建一个容积为104m3
的圆柱形煤气储存室。
(1)储存室的底面积S(单位:m2)与其深度d(单位:m)有怎样的函数关系?
解:
根据圆柱体的体积公式,得
Sd=104
变形得:
即储存室的底面积S是其深度d的反比例函数。
例题讲解
(2)公司决定把储存室的底面积S定为500
m2
,施工队施工时应该向下掘进多深?
已知函数值求自变量的值
解:
,
把S=500代入
得:
解得:
如果把储存室的底面积
定为500m2,
施工时应向地下掘进
20m深。
例题讲解
相应地,储存室的底面积应改为多少?
(结果保留小数点后两位)
已知自变量的值求函数值
(3)当施工队按(2)中的计划掘进到地下15m时,公司临时改变计划,
把储存室的深度改为15m。
解:
根据题意,把d=15代入
得:
解得:
S≈666.67
(
㎡)
当储存室的深度为15m时,
储存室的底面积应改为666.67m2。
巩固练习
教材P15练习1
如图,某玻璃器皿制造公司要制造一种容积为1L(1L=1dm3)的圆锥形漏斗。
(1)漏斗口的面积S
与漏斗的深d
有怎样的函数关系?
(2)如果漏斗口的面积为100cm2,则漏斗的深为多少?
d=3(dm)
例题讲解
例2
码头工人每天往一艘轮船上装载30吨货物,
装载完毕恰好用了8天时间。
例题讲解
(1)轮船到达目的地后开始卸货,卸货速度v(单位:吨/天)与卸货时间t(单位:天)之间有怎样的函数关系?
解:
设轮船上的货物总量为k吨,
则根据已知条件有
k=30×8=240
所以v与t的函数式为
例题讲解
(2)由于遇到紧急情况,要求船上的货物不超过5天卸载完毕,
那么平均每天至少要卸多少吨货物?
解:
把t=5代入
,得
从结果可以看出,如果全部货物恰好用5天卸完,则平均每天卸载48吨。当t>0时,t
越小,v
越大。若货物在不超过5天内卸完,则平均每天至少要卸货48吨。
例题讲解
(3)在直角坐标系中作出相应的函数图象。
t
…
…
v
…
…
5
10
15
20
25
48
24
16
12
9.6
大家知道反比例函数的图象
是两条曲线,上题中图象的曲线
是在哪个象限,
请大家讨论一下?
O
5
10
10
20
30
40
50
60
15
20
25
t
(天)
v(吨/天)
48
例题讲解
O
5
10
10
20
30
40
50
60
15
20
25
t
(天)
v(吨/天)
48
(4)请利用图象对(2)做出直观解释。
解:
由图象可知,
若货物在不超过5天内卸完,
则平均每天至少要卸货48吨。
巩固练习
1.一个圆柱体的侧面展开图是一个面积为10的矩形,这个圆柱的高h与底面半径r之间的函数关系是(
)
A.正比例函数
B.一次函数
C.反比例函数
D.函数关系不确定
C
2.已知矩形的面积为10,则它的长y与宽x之间的关系用图象大致可表示为
(
)
A
巩固练习
3.面积为2的△ABC,一边长为x,这边上的高为y,则y与x的变化规律用图象表示大致是(
)
C
例题讲解
知识点二
用反比例函数解决物理问题
例题讲解
例3
小伟欲用撬棍撬动一块大石头,已知阻力和阻力臂不变,分别为1200牛顿和0.5米。
(1)
动力F与动力臂l
有怎样的函数关系?
当动力臂为1.5米时,撬动石头至少需要多大的力?
解:
根据“杠杆定律”,有Fl
=
,
∴
F与l
的函数解析式为:F=
,
当l=1.5时,F=
,
∴
撬动石头至少需要
牛顿的力。
1200×0.5
400
400
例题讲解
(2)若想使动力F不超过题(1)中所用力的一半,则动力臂至少要加长多少?
由(1)可知Fl=600,得函数解析式l
=
,
当F=
=
时,l
=
=
,
∴
-1.5=
,
答:若想用力不超过400牛顿的一半,则动力臂至少要加长
米。
例题讲解
例4
一个用电器的电阻是可以调节的,
其范围为110~220欧姆,
已知电压为220伏,
这个用电器的电路图如图所示。
(1)输出功率P与电阻R有怎样的函数关系?
解:
根据电学知识,
当U=220时,有P=
∴
输出功率P是电阻R的反比例函数,
解析式为:P=
①
例题讲解
(2)这个用电器输出功率的范围多大?
从①式可以看出,电阻越大,功率越小。
把电阻的最小值R=110代入①式,得到输出功率
的最大值P=
把电阻的最大值R=220代入①
式,则得到输出功率的最小值,P=
∴
用电器的输出功率在
瓦到
瓦之间。
解:
例题讲解
为什么收音机的音量、某些台灯的亮度以及电风扇的转速
可以调节?
思
考
因为电压不变时,
输出功率P是电阻R的反比例函数,
通过调节电器的电阻可以改变功率,
电阻越大,功率越小。
归纳
实际问题
反比例函数
建立数学模型
运用数学知识解决
巩固练习
1.某闭合电路中,电源的电压为定值,电流I(A)与电阻R(Ω)成反比例。
下图表示的是该电路中电流I与电阻R之间的图象,
则用电阻R表示电流I的函数解析式为(
)
C
巩固练习
2.甲、乙两地相距100千米,汽车从甲地到乙地所用的时间y
(小时)与行驶的平均速度x
(千米/小时)的函数图象大致是(
)
A
B
C
D
B
巩固练习
3.物理学知识告诉D我们,一个物体所受到的压强P
与所受压力F及受力面积S之间的计算公式为
。
当一个物体所受压力为定值时,那么该物体所受压强P与受力面积S
之间的关系用图象表示大致为(
)。
O
P
S
O
P
O
P
S
O
P
S
S
A
B
C
D
C
课堂小结
1.长方体中当体积V一定时,高h与底面积S的关系
。
2.在工程问题中,当
一定时,
与
成反比例,即
3.学习反思:
工作量
时间
工作效率
课堂小结
1.在我们使用撬棍时,动力臂越
(填长或短)就越省力。
2.用电器的输出功率P(瓦)、两端电压U(伏)及用电器的电阻R
(欧姆)的关系:
或
或
3、学习反思:
长
反比例函数
26
26.2
实际问题与反比例函数
学习目标
教学分析
1.经历在具体问题中探究反比例函数应用的过程,体会反比例函数作为一种数学模型的意义。
2.利用反比例函数的知识分析和解决实际问题。
3.渗透数形结合思想,提高用函数观点解决问题的能力。
复习回顾
反比例函数的性质
当k>0时,双曲线的两支分别在第一、三象限,
在每一个象限内,y随x的增大而减小;
当k<0时,双曲线的两支分别在第二、四象限,
在每一个象限内,y随x的增大而增大。
复习回顾
双曲线不过原点且与两坐标轴永不相交,但无限靠近x
轴、y
轴。
反比例函数的性质
反比例函数的图象既是中心对称图形,又是轴对称图形;
对称中心是原点,有两条对称轴。
复习回顾
反比例函数与一次函数综合应用
1.
如图,一次函数y1=x-1与反比例函数y2=
的图象交于点A(2,1),
B(-1,-2),则使y1
>y2的x
的取值范围是(
)。
x>2
B.
x>2
或-1<x<0
C.
-1<x<2
D.
x>2
或x<-1
B
复习回顾
2.
如图,已知A(-4,2)、B(n,-4)是一次函数的图象
与反比例函数的图象的两个交点。
(1)求此反比例函数和一次函数的解析式;
一次函数的解析式:
y=-x-2
反比例函数解析式:
复习回顾
(2)
根据图象写出使一次函数的值小于
反比例函数的值的x的取值范围。
x的取值范围为:
分类讨论
1.如图表示
)
(
—
=
x
k
y
1
和
y
)
0
(
?
=
k
x
k
在同一坐标系中的大致
图象的是(
)。
D
O
x
y
A
C
O
x
y
D
x
y
o
O
x
y
B
解题思路:
k
kx
y
+
=
-
)
x
k
y
-
=
1
(
数形结合
2.
已知点A(2,y1),B(5,y2),C(-3,y3)是反比例函数
图象上的三点。
请比较y1,y2,y3的大小。
x
y
O
2
5
y1
y2
A
B
y3
C
-3
(1)代入求值。
(2)利用增减性。
(3)根据图象判断。
例题讲解
知识点一
用反比例函数解决体积问题
例题讲解
例1
市煤气公司要在地下修建一个容积为104m3
的圆柱形煤气储存室。
(1)储存室的底面积S(单位:m2)与其深度d(单位:m)有怎样的函数关系?
解:
根据圆柱体的体积公式,得
Sd=104
变形得:
即储存室的底面积S是其深度d的反比例函数。
例题讲解
(2)公司决定把储存室的底面积S定为500
m2
,施工队施工时应该向下掘进多深?
已知函数值求自变量的值
解:
,
把S=500代入
得:
解得:
如果把储存室的底面积
定为500m2,
施工时应向地下掘进
20m深。
例题讲解
相应地,储存室的底面积应改为多少?
(结果保留小数点后两位)
已知自变量的值求函数值
(3)当施工队按(2)中的计划掘进到地下15m时,公司临时改变计划,
把储存室的深度改为15m。
解:
根据题意,把d=15代入
得:
解得:
S≈666.67
(
㎡)
当储存室的深度为15m时,
储存室的底面积应改为666.67m2。
巩固练习
教材P15练习1
如图,某玻璃器皿制造公司要制造一种容积为1L(1L=1dm3)的圆锥形漏斗。
(1)漏斗口的面积S
与漏斗的深d
有怎样的函数关系?
(2)如果漏斗口的面积为100cm2,则漏斗的深为多少?
d=3(dm)
例题讲解
例2
码头工人每天往一艘轮船上装载30吨货物,
装载完毕恰好用了8天时间。
例题讲解
(1)轮船到达目的地后开始卸货,卸货速度v(单位:吨/天)与卸货时间t(单位:天)之间有怎样的函数关系?
解:
设轮船上的货物总量为k吨,
则根据已知条件有
k=30×8=240
所以v与t的函数式为
例题讲解
(2)由于遇到紧急情况,要求船上的货物不超过5天卸载完毕,
那么平均每天至少要卸多少吨货物?
解:
把t=5代入
,得
从结果可以看出,如果全部货物恰好用5天卸完,则平均每天卸载48吨。当t>0时,t
越小,v
越大。若货物在不超过5天内卸完,则平均每天至少要卸货48吨。
例题讲解
(3)在直角坐标系中作出相应的函数图象。
t
…
…
v
…
…
5
10
15
20
25
48
24
16
12
9.6
大家知道反比例函数的图象
是两条曲线,上题中图象的曲线
是在哪个象限,
请大家讨论一下?
O
5
10
10
20
30
40
50
60
15
20
25
t
(天)
v(吨/天)
48
例题讲解
O
5
10
10
20
30
40
50
60
15
20
25
t
(天)
v(吨/天)
48
(4)请利用图象对(2)做出直观解释。
解:
由图象可知,
若货物在不超过5天内卸完,
则平均每天至少要卸货48吨。
巩固练习
1.一个圆柱体的侧面展开图是一个面积为10的矩形,这个圆柱的高h与底面半径r之间的函数关系是(
)
A.正比例函数
B.一次函数
C.反比例函数
D.函数关系不确定
C
2.已知矩形的面积为10,则它的长y与宽x之间的关系用图象大致可表示为
(
)
A
巩固练习
3.面积为2的△ABC,一边长为x,这边上的高为y,则y与x的变化规律用图象表示大致是(
)
C
例题讲解
知识点二
用反比例函数解决物理问题
例题讲解
例3
小伟欲用撬棍撬动一块大石头,已知阻力和阻力臂不变,分别为1200牛顿和0.5米。
(1)
动力F与动力臂l
有怎样的函数关系?
当动力臂为1.5米时,撬动石头至少需要多大的力?
解:
根据“杠杆定律”,有Fl
=
,
∴
F与l
的函数解析式为:F=
,
当l=1.5时,F=
,
∴
撬动石头至少需要
牛顿的力。
1200×0.5
400
400
例题讲解
(2)若想使动力F不超过题(1)中所用力的一半,则动力臂至少要加长多少?
由(1)可知Fl=600,得函数解析式l
=
,
当F=
=
时,l
=
=
,
∴
-1.5=
,
答:若想用力不超过400牛顿的一半,则动力臂至少要加长
米。
例题讲解
例4
一个用电器的电阻是可以调节的,
其范围为110~220欧姆,
已知电压为220伏,
这个用电器的电路图如图所示。
(1)输出功率P与电阻R有怎样的函数关系?
解:
根据电学知识,
当U=220时,有P=
∴
输出功率P是电阻R的反比例函数,
解析式为:P=
①
例题讲解
(2)这个用电器输出功率的范围多大?
从①式可以看出,电阻越大,功率越小。
把电阻的最小值R=110代入①式,得到输出功率
的最大值P=
把电阻的最大值R=220代入①
式,则得到输出功率的最小值,P=
∴
用电器的输出功率在
瓦到
瓦之间。
解:
例题讲解
为什么收音机的音量、某些台灯的亮度以及电风扇的转速
可以调节?
思
考
因为电压不变时,
输出功率P是电阻R的反比例函数,
通过调节电器的电阻可以改变功率,
电阻越大,功率越小。
归纳
实际问题
反比例函数
建立数学模型
运用数学知识解决
巩固练习
1.某闭合电路中,电源的电压为定值,电流I(A)与电阻R(Ω)成反比例。
下图表示的是该电路中电流I与电阻R之间的图象,
则用电阻R表示电流I的函数解析式为(
)
C
巩固练习
2.甲、乙两地相距100千米,汽车从甲地到乙地所用的时间y
(小时)与行驶的平均速度x
(千米/小时)的函数图象大致是(
)
A
B
C
D
B
巩固练习
3.物理学知识告诉D我们,一个物体所受到的压强P
与所受压力F及受力面积S之间的计算公式为
。
当一个物体所受压力为定值时,那么该物体所受压强P与受力面积S
之间的关系用图象表示大致为(
)。
O
P
S
O
P
O
P
S
O
P
S
S
A
B
C
D
C
课堂小结
1.长方体中当体积V一定时,高h与底面积S的关系
。
2.在工程问题中,当
一定时,
与
成反比例,即
3.学习反思:
工作量
时间
工作效率
课堂小结
1.在我们使用撬棍时,动力臂越
(填长或短)就越省力。
2.用电器的输出功率P(瓦)、两端电压U(伏)及用电器的电阻R
(欧姆)的关系:
或
或
3、学习反思:
长
