人教B版(2019)必修(第四册)第十一章 立体几何初步11.1 空间几何体多面体与棱柱(50张PPT)
文档属性
| 名称 | 人教B版(2019)必修(第四册)第十一章 立体几何初步11.1 空间几何体多面体与棱柱(50张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 7.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-20 10:46:03 | ||
图片预览









文档简介
(共50张PPT)
高一年级
数学
多面体与棱柱
知识概要
一、多面体的定义和分类
二、多面体的基本元素
三、棱柱的定义和基本元素
四、棱柱的分类
知识概要
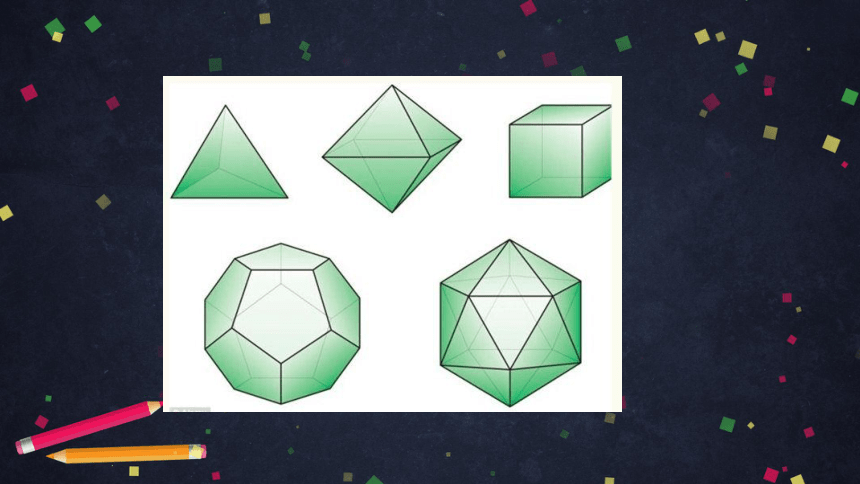
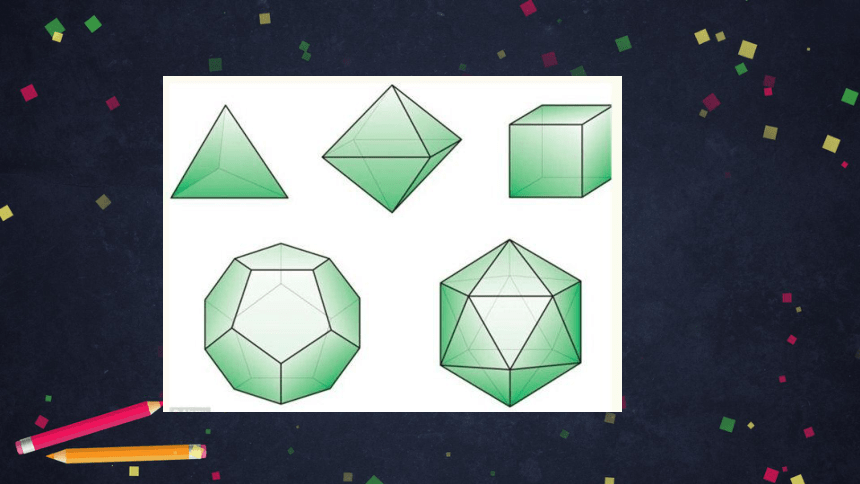
古希腊人研究过下面形状的几何体,并且把它们用阿基米德的名字命名.同学们看一看,这些几何体有什么共同点?
这些几何体都是由若干个平面围成的,几何体的每个面都是平面多边形.
多面体的定义
由若干个平面多边形所围成的封闭几何体称为多面体.
把多面体的任意一个面延展为平面,如果其余的各面都在这个平面的同一侧,则称这样的多面体为凸多面体.我们目前所学的多面体都指凸多面体.
多面体的分类
多面体可以按照围成它的面的个数来分类.
想一想,多面体最少有几个面?
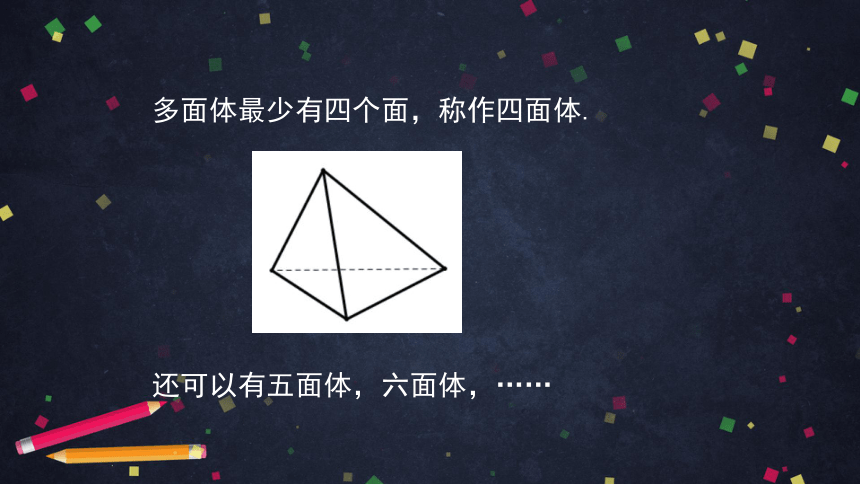
多面体最少有四个面,称作四面体.
还可以有五面体,六面体,……
多面体的基本元素
围成多面体的各个多边形称为多面体的面,
相邻两个面的公共边称为多面体的棱,
棱与棱的公共点称为多面体的顶点.
顶点
棱
面
多面体的基本元素
多面体中,连接同一个面上两个顶点的线段,如果不是多面体的棱,就称为多面体的面对角线
连接不在同一面上两个顶点的线段称为多面体的体对角线
一个多面体和一个平面相交所得到的平面图形(包含它的内部),称为多面体的一个截面
例.如图是由长方体截掉一个角得到的多面体.
(1)分别写出这个多面体顶点,棱和面的个数;
(2)写出这个多面体的一条面对角线和体对角线;
(3)判断直线BE与面ABCD的位置关系.
例.如图是由长方体截掉一个角得到的多面体.
(1)分别写出这个多面体顶点,棱和面的个数;
例.如图是由长方体截掉一个角得到的多面体.
(1)分别写出这个多面体顶点,棱和面的个数;
共有10个顶点,15条棱,7个面
例.如图是由长方体截掉一个角得到的多面体.
(2)写出这个多面体的一条面对角线和体对角线;
例.如图是由长方体截掉一个角得到的多面体.
(2)写出这个多面体的一条面对角线和体对角线;
面对角线:AC,AE,AN等
体对角线:AM,AC'等
例.如图是由长方体截掉一个角得到的多面体.
(3)判断直线BE与面ABCD的位置关系.
例.如图是由长方体截掉一个角得到的多面体.
(3)判断直线BE与面ABCD的位置关系.
直线BE与面ABCD有公共点B,它们是相交的关系
我们再来看一看,下面这些几何体都是多面体吗?它们还有什么共同点?
棱柱的定义
一般地,有两个面互相平行,且该多面体的顶点都在这两个面上,其余各面都是平行四边形,这样的多面体称为棱柱.
想一想,如果去掉“该多面体的顶点都在这两个面上”这个条件可以吗?
不可以,左图就是一个反例.
棱柱的基本元素
棱柱的两个互相平行的面称为棱柱的底面,其他各面称为棱柱的侧面,两个侧面的公共边称为侧棱.
过棱柱一个底面上的任意一个顶点,作另一个底面的垂线所得到的线段称为棱柱的高.
底面
侧面
侧棱
棱柱的基本元素
学习了底面,侧面,侧棱的概念之后,
棱柱的定义可以描述为:
①底面平行
②侧面是平行四边形
③顶点都在底面上
棱柱的分类
按底面形状:三棱柱,四棱柱,……
斜棱柱:侧棱不垂直于底面
棱柱
直棱柱:侧棱垂直于底面
正棱柱:底面是正多边形的直棱柱
……
棱柱的分类
按侧棱与底面的关系:
棱柱的分类
直棱柱的侧面都是矩形
直棱柱的侧棱与高长度相等
棱柱的分类
平行六面体:底面为平行四边形的棱柱
直平行六面体:侧棱与底面垂直的平行六面体
棱柱的分类
想一想,
①底面是矩形的平行六面体就是长方体,对吗?
②正四棱柱一定是直平行六面体吗?
棱柱的分类
底面是矩形的平行六面体,它的侧棱不一定与底面垂直,因此侧面只能确定是平行四边形,不一定是矩形,所以它不是长方体.
棱柱的分类
正四棱柱的底面为正方形,正方形是特殊的平行四边形,因此它是平行六面体.
又因为正四棱柱也是直四棱柱,它的侧棱垂直于底面,因此也是直平行六面体.
例.如图是一个底面为正三角形的三棱柱ABC-A'B'C'.
(1)写出这个三棱柱的所有底面和侧面;
(2)这个三棱柱一定是正三棱柱吗?请说明理由.
例.如图是一个底面为正三角形的三棱柱.
(1)写出这个三棱柱的所有底面和侧面;
底面:面ABC,面A'B'C'
侧面:面ABB'A',面ACC'A',
面BCC'B'
例.如图是一个底面为正三角形的三棱柱.
(2)这个三棱柱一定是正三棱柱吗?请说明理由.
不一定,因为侧棱和底面不一定垂直.
例.如图是一个底面为菱形的直四棱柱,AB=1,AA'=2.
(1)判断直线AB与CC',直线AB与A'B'的位置关系;
(2)求面对角线AB'的长;
(3)求这个四棱柱的侧面积;
例.如图是一个底面为菱形的直四棱柱,AB=1,AA'=2.
(4)若
,求体对角线AC'的长.
例.如图是一个底面为菱形的直四棱柱,AB=1,AA'=2.
(1)判断直线AB与CC',直线AB与A'B'的位置关系;
直线AB与CC'异面
直线AB与A'B'平行
例.如图是一个底面为菱形的直四棱柱,AB=1,AA'=2.
(2)求面对角线AB'的长;
直棱柱的侧棱垂直于底面,侧面ABB'A'为矩形,由AB=1,AA'
=2得AB'
=
例.如图是一个底面为菱形的直四棱柱,AB=1,AA'=2.
(3)求这个四棱柱的侧面积.
侧面积:所有侧面面积之和
底面积:所有底面面积之和
表面积:围成多面体的所有面面积之和
例.如图是一个底面为菱形的直四棱柱,AB=1,AA'=2.
(3)求这个四棱柱的侧面积.
这个四棱柱的四个侧面都是矩形,侧面积=4×1×2=8
例.如图是一个底面为菱形的直四棱柱,AB=1,AA'=2.
(4)若
,求体对角线AC'的长.
连接AC,AC',在三角形ACD中,由AD=CD=1,
可以求得AC=
例.如图是一个底面为菱形的直四棱柱,AB=1,AA'=2.
侧棱与底面垂直,因此也垂直于底面内的直线,所以CC'垂直于AC,在直角三角形ACC'中,可
以求得
小
结
一、多面体的定义,顶点,棱,面,对角线
二、棱柱的定义,底面,侧面,侧棱,分类
作
业
课本70页练习A
2,3;练习B
2,3,4
谢谢聆听!
高一年级
数学
多面体与棱柱
知识概要
一、多面体的定义和分类
二、多面体的基本元素
三、棱柱的定义和基本元素
四、棱柱的分类
知识概要
古希腊人研究过下面形状的几何体,并且把它们用阿基米德的名字命名.同学们看一看,这些几何体有什么共同点?
这些几何体都是由若干个平面围成的,几何体的每个面都是平面多边形.
多面体的定义
由若干个平面多边形所围成的封闭几何体称为多面体.
把多面体的任意一个面延展为平面,如果其余的各面都在这个平面的同一侧,则称这样的多面体为凸多面体.我们目前所学的多面体都指凸多面体.
多面体的分类
多面体可以按照围成它的面的个数来分类.
想一想,多面体最少有几个面?
多面体最少有四个面,称作四面体.
还可以有五面体,六面体,……
多面体的基本元素
围成多面体的各个多边形称为多面体的面,
相邻两个面的公共边称为多面体的棱,
棱与棱的公共点称为多面体的顶点.
顶点
棱
面
多面体的基本元素
多面体中,连接同一个面上两个顶点的线段,如果不是多面体的棱,就称为多面体的面对角线
连接不在同一面上两个顶点的线段称为多面体的体对角线
一个多面体和一个平面相交所得到的平面图形(包含它的内部),称为多面体的一个截面
例.如图是由长方体截掉一个角得到的多面体.
(1)分别写出这个多面体顶点,棱和面的个数;
(2)写出这个多面体的一条面对角线和体对角线;
(3)判断直线BE与面ABCD的位置关系.
例.如图是由长方体截掉一个角得到的多面体.
(1)分别写出这个多面体顶点,棱和面的个数;
例.如图是由长方体截掉一个角得到的多面体.
(1)分别写出这个多面体顶点,棱和面的个数;
共有10个顶点,15条棱,7个面
例.如图是由长方体截掉一个角得到的多面体.
(2)写出这个多面体的一条面对角线和体对角线;
例.如图是由长方体截掉一个角得到的多面体.
(2)写出这个多面体的一条面对角线和体对角线;
面对角线:AC,AE,AN等
体对角线:AM,AC'等
例.如图是由长方体截掉一个角得到的多面体.
(3)判断直线BE与面ABCD的位置关系.
例.如图是由长方体截掉一个角得到的多面体.
(3)判断直线BE与面ABCD的位置关系.
直线BE与面ABCD有公共点B,它们是相交的关系
我们再来看一看,下面这些几何体都是多面体吗?它们还有什么共同点?
棱柱的定义
一般地,有两个面互相平行,且该多面体的顶点都在这两个面上,其余各面都是平行四边形,这样的多面体称为棱柱.
想一想,如果去掉“该多面体的顶点都在这两个面上”这个条件可以吗?
不可以,左图就是一个反例.
棱柱的基本元素
棱柱的两个互相平行的面称为棱柱的底面,其他各面称为棱柱的侧面,两个侧面的公共边称为侧棱.
过棱柱一个底面上的任意一个顶点,作另一个底面的垂线所得到的线段称为棱柱的高.
底面
侧面
侧棱
棱柱的基本元素
学习了底面,侧面,侧棱的概念之后,
棱柱的定义可以描述为:
①底面平行
②侧面是平行四边形
③顶点都在底面上
棱柱的分类
按底面形状:三棱柱,四棱柱,……
斜棱柱:侧棱不垂直于底面
棱柱
直棱柱:侧棱垂直于底面
正棱柱:底面是正多边形的直棱柱
……
棱柱的分类
按侧棱与底面的关系:
棱柱的分类
直棱柱的侧面都是矩形
直棱柱的侧棱与高长度相等
棱柱的分类
平行六面体:底面为平行四边形的棱柱
直平行六面体:侧棱与底面垂直的平行六面体
棱柱的分类
想一想,
①底面是矩形的平行六面体就是长方体,对吗?
②正四棱柱一定是直平行六面体吗?
棱柱的分类
底面是矩形的平行六面体,它的侧棱不一定与底面垂直,因此侧面只能确定是平行四边形,不一定是矩形,所以它不是长方体.
棱柱的分类
正四棱柱的底面为正方形,正方形是特殊的平行四边形,因此它是平行六面体.
又因为正四棱柱也是直四棱柱,它的侧棱垂直于底面,因此也是直平行六面体.
例.如图是一个底面为正三角形的三棱柱ABC-A'B'C'.
(1)写出这个三棱柱的所有底面和侧面;
(2)这个三棱柱一定是正三棱柱吗?请说明理由.
例.如图是一个底面为正三角形的三棱柱.
(1)写出这个三棱柱的所有底面和侧面;
底面:面ABC,面A'B'C'
侧面:面ABB'A',面ACC'A',
面BCC'B'
例.如图是一个底面为正三角形的三棱柱.
(2)这个三棱柱一定是正三棱柱吗?请说明理由.
不一定,因为侧棱和底面不一定垂直.
例.如图是一个底面为菱形的直四棱柱,AB=1,AA'=2.
(1)判断直线AB与CC',直线AB与A'B'的位置关系;
(2)求面对角线AB'的长;
(3)求这个四棱柱的侧面积;
例.如图是一个底面为菱形的直四棱柱,AB=1,AA'=2.
(4)若
,求体对角线AC'的长.
例.如图是一个底面为菱形的直四棱柱,AB=1,AA'=2.
(1)判断直线AB与CC',直线AB与A'B'的位置关系;
直线AB与CC'异面
直线AB与A'B'平行
例.如图是一个底面为菱形的直四棱柱,AB=1,AA'=2.
(2)求面对角线AB'的长;
直棱柱的侧棱垂直于底面,侧面ABB'A'为矩形,由AB=1,AA'
=2得AB'
=
例.如图是一个底面为菱形的直四棱柱,AB=1,AA'=2.
(3)求这个四棱柱的侧面积.
侧面积:所有侧面面积之和
底面积:所有底面面积之和
表面积:围成多面体的所有面面积之和
例.如图是一个底面为菱形的直四棱柱,AB=1,AA'=2.
(3)求这个四棱柱的侧面积.
这个四棱柱的四个侧面都是矩形,侧面积=4×1×2=8
例.如图是一个底面为菱形的直四棱柱,AB=1,AA'=2.
(4)若
,求体对角线AC'的长.
连接AC,AC',在三角形ACD中,由AD=CD=1,
可以求得AC=
例.如图是一个底面为菱形的直四棱柱,AB=1,AA'=2.
侧棱与底面垂直,因此也垂直于底面内的直线,所以CC'垂直于AC,在直角三角形ACC'中,可
以求得
小
结
一、多面体的定义,顶点,棱,面,对角线
二、棱柱的定义,底面,侧面,侧棱,分类
作
业
课本70页练习A
2,3;练习B
2,3,4
谢谢聆听!
