人教B版(2019)必修(第四册) 11.1.4棱锥与棱台 课件(47张PPT)
文档属性
| 名称 | 人教B版(2019)必修(第四册) 11.1.4棱锥与棱台 课件(47张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 8.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-20 10:50:19 | ||
图片预览









文档简介
(共47张PPT)
高一年级
数学
棱锥与棱台
知识概要
一、棱锥的定义和分类
二、棱台的定义和分类
知识概要
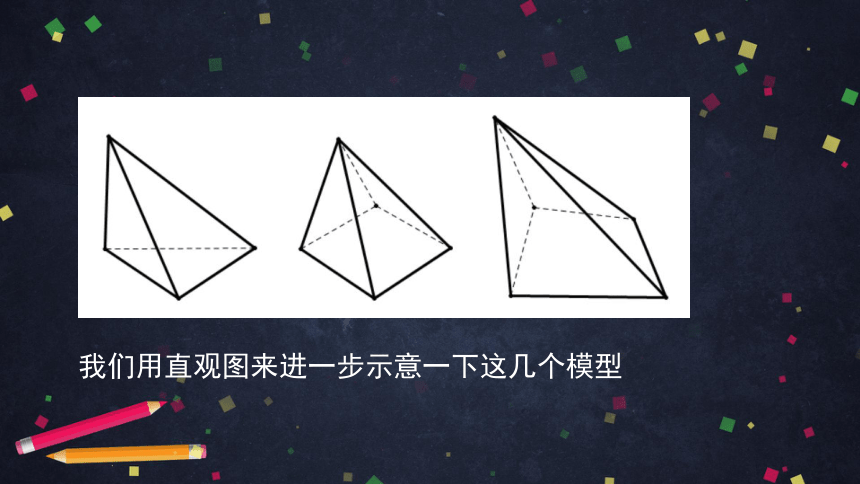
这是几位同学自己动手制作的模型,请大家看一看,这些几何体有什么共同的特征?
我们用直观图来进一步示意一下这几个模型
一个面是多边形
其余各面是三角形
各三角形面有公共顶点
棱锥的定义
有一个面是多边形,其余各面都是有一个公共顶点的三角形,则称这个多面体为棱锥.
棱锥的定义
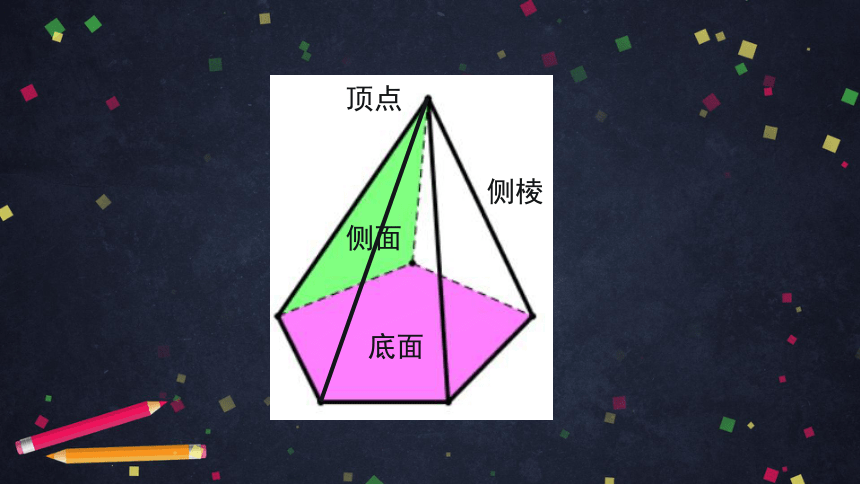
棱锥中,是多边形的那个面称为棱锥的底面,
有公共顶点的各三角形称为棱锥的侧面,
各侧面的公共顶点称为棱锥的顶点,
相邻两侧面的公共边称为棱锥的侧棱.
过棱锥的顶点作棱锥底面的垂线,得到的线段称为棱锥的高.
顶点
侧面
底面
侧棱
棱锥的定义
棱锥的特征
①底面为多边形
②侧面为三角形
③侧面共顶点
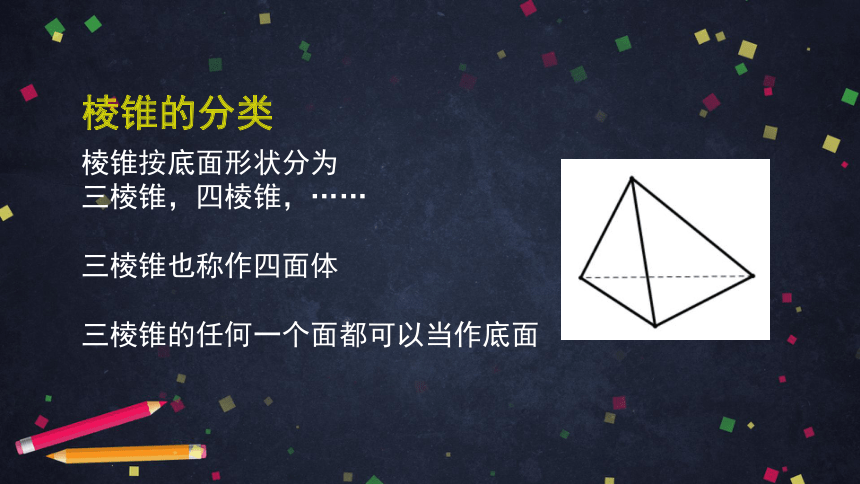
棱锥的分类
棱锥按底面形状分为
三棱锥,四棱锥,……
三棱锥也称作四面体
三棱锥的任何一个面都可以当作底面
棱锥的分类
如果棱锥的底面是正多边形,且棱锥的顶点与底面中心连线垂直于底面,则称这个棱锥为正棱锥.
想一想,去掉“棱锥的顶点与底面中心连线垂直于底面”这个条件,会出现什么情况?
o
棱锥的分类
正棱锥的侧面是全等的等腰三角形,它们底边上的高都相等,称作正棱锥的斜高.
想一想,正棱锥的高与斜高有什么关系呢?
OP为正四棱锥P-ABCD的高
PM为正四棱锥P-ABCD的斜高
在直角三角形OPM中,可得
斜高>高
例.在正四棱锥P-ABCD中,设底面边长为2,侧棱长为3.
(1)求棱锥的斜高与高;
(2)求棱锥的表面积.
例.在正四棱锥P-ABCD中,设底面边长为2,侧棱长为3.
(1)求棱锥的斜高与高;
在直角三角形PBM中,
在直角三角形POM中,
例.在正四棱锥P-ABCD中,设底面边长为2,侧棱长为3.
(1)求棱锥的斜高与高;
也可以这样计算高
在直角三角形ABD中,
在直角三角形POB中,
例.在正四棱锥P-ABCD中,设底面边长为2,侧棱长为3.
(2)求棱锥的表面积.
回忆表面积:围成多面体的所有面面积之和.
例.在正四棱锥P-ABCD中,设底面边长为2,侧棱长为3.
(2)求棱锥的表面积.
棱锥有四个侧面,是全等的等腰三角形,一个底面,为正方形.
例.在正四棱锥P-ABCD中,设底面边长为2,侧棱长为3.
(2)求棱锥的表面积.
例.如果一个棱锥侧面是全等的等腰三角形,它一定是正棱锥吗?试着说明理由.
例.如果一个棱锥侧面是全等的等腰三角形,它一定是正棱锥吗?试着说明理由.
不一定.我们来看下面的反例.
2
2
2
2
1
1
棱台的定义
用平行于棱锥底面的平面去截棱锥,所得截面与底面间的多面体称为棱台.
棱台的定义
原棱锥的底面与截面分别称为棱台的下底面与上底面,
其余各面称为棱台的侧面,
相邻两侧面的公共边称为棱台的侧棱.
棱台的定义
上底面
下底面
侧面
侧棱
棱台的定义
棱台的特征
①由棱锥截得
②底面为多边形
③底面平行
④侧面为梯形
注意:棱台必须能还原成棱锥,左图不是棱台
棱台的定义
过棱台一个底面上的任意一个顶点,作另一个底面的垂线所得到的线段称为棱台的高.
棱台的分类
棱台也可以分为三棱台,四棱台,……
由正棱锥截得的棱台称为正棱台.
正棱台的侧面都是全等的等腰梯形,这些等腰梯形的高都相等,称作正棱台的斜高.
例.在正三棱台A'B'C'-ABC中,上底面边长和侧棱都为1,下底面边长为2.
(1)求棱台的斜高;
(2)求棱台的高.
例.在正三棱台A'B'C'-ABC中,上底面边长和侧棱都为1,下底面边长为2.
(1)在侧面的梯形ACC'A'中,
作A'E,C'F垂直于AC,
由AC=2,A'C'=1可知AE=CF=
,
又AA'=1,从而A'E=
,
即斜高为
E
F
例.在正三棱台A'B'C'-ABC中,上底面边长和侧棱都为1,下底面边长为2.
(2)将正三棱台还原为正三棱锥
P-ABC,连接P和底面中心O,则OP与面A'B'C'的交点恰为上底面中心O'
P
O'
O
例.在正三棱台A'B'C'-ABC中,上底面边长和侧棱都为1,下底面边长为2.
(2)在等边三角形ABC中,由于
AB=2,可以计算出OC=
同理O'C'=
P
O'
O
例.在正三棱台A'B'C'-ABC中,上底面边长和侧棱都为1,下底面边长为2.
只看等边三角形ABC,由于
AB=2,所以CD=1,又
在三角形COD中,
E
例.在正三棱台A'B'C'-ABC中,上底面边长和侧棱都为1,下底面边长为2.
OC=
,同理O'C'=
,
在三角形POC中,O'C'为中位线,
于是PC=2CC'=2
P
O'
O
例.在正三棱台A'B'C'-ABC中,上底面边长和侧棱都为1,下底面边长为2.
所以高为
P
O'
O
棱柱棱锥棱台的特征
棱柱
棱锥
棱台
①底面平行
②侧面是平行四边形
③顶点在底面上
①底面为多边形
②侧面为三角形
③侧面共顶点
①由棱锥截得
②底面为多边形
③底面平行
④侧面为梯形
我们一般是从点、线、面这些基本元素入手,用它们的形状、大小与位置关系去刻画几何体的结构特征.
例如形状:底面多边形,侧面三角形,……
位置关系:底面平行,侧面共顶点,……
棱柱棱锥棱台的特征
让我们再想一想,我们在这两节课的学习中,都碰到了哪些点线面之间的位置关系?
棱柱棱锥棱台的特征
平面与平面平行:棱柱或棱台的两个底面
平面与平面相交:棱锥的各个侧面
棱柱棱锥棱台的特征
直线与平面平行:棱柱或棱台一个底面中的边与另一个底面
直线与平面相交:侧棱与底面
直线在平面内:侧棱在侧面内
棱柱棱锥棱台的特征
直线与直线平行,直线与直线相交,直线与直线异面,同学们可以课下自己找一找.
棱柱棱锥棱台的特征
棱柱棱锥棱台的分类
棱柱
棱锥
棱台
斜棱柱
直棱柱
正棱锥
……
正棱台
……
……
正棱柱
……
小
结
一、棱锥的定义,顶点,底面,侧面,侧棱
二、棱台的定义,底面,侧面,侧棱
三、棱柱、棱锥、棱台的特征与分类对比
作
业
课本75页练习A
2,3,4,5
谢谢聆听!
高一年级
数学
棱锥与棱台
知识概要
一、棱锥的定义和分类
二、棱台的定义和分类
知识概要
这是几位同学自己动手制作的模型,请大家看一看,这些几何体有什么共同的特征?
我们用直观图来进一步示意一下这几个模型
一个面是多边形
其余各面是三角形
各三角形面有公共顶点
棱锥的定义
有一个面是多边形,其余各面都是有一个公共顶点的三角形,则称这个多面体为棱锥.
棱锥的定义
棱锥中,是多边形的那个面称为棱锥的底面,
有公共顶点的各三角形称为棱锥的侧面,
各侧面的公共顶点称为棱锥的顶点,
相邻两侧面的公共边称为棱锥的侧棱.
过棱锥的顶点作棱锥底面的垂线,得到的线段称为棱锥的高.
顶点
侧面
底面
侧棱
棱锥的定义
棱锥的特征
①底面为多边形
②侧面为三角形
③侧面共顶点
棱锥的分类
棱锥按底面形状分为
三棱锥,四棱锥,……
三棱锥也称作四面体
三棱锥的任何一个面都可以当作底面
棱锥的分类
如果棱锥的底面是正多边形,且棱锥的顶点与底面中心连线垂直于底面,则称这个棱锥为正棱锥.
想一想,去掉“棱锥的顶点与底面中心连线垂直于底面”这个条件,会出现什么情况?
o
棱锥的分类
正棱锥的侧面是全等的等腰三角形,它们底边上的高都相等,称作正棱锥的斜高.
想一想,正棱锥的高与斜高有什么关系呢?
OP为正四棱锥P-ABCD的高
PM为正四棱锥P-ABCD的斜高
在直角三角形OPM中,可得
斜高>高
例.在正四棱锥P-ABCD中,设底面边长为2,侧棱长为3.
(1)求棱锥的斜高与高;
(2)求棱锥的表面积.
例.在正四棱锥P-ABCD中,设底面边长为2,侧棱长为3.
(1)求棱锥的斜高与高;
在直角三角形PBM中,
在直角三角形POM中,
例.在正四棱锥P-ABCD中,设底面边长为2,侧棱长为3.
(1)求棱锥的斜高与高;
也可以这样计算高
在直角三角形ABD中,
在直角三角形POB中,
例.在正四棱锥P-ABCD中,设底面边长为2,侧棱长为3.
(2)求棱锥的表面积.
回忆表面积:围成多面体的所有面面积之和.
例.在正四棱锥P-ABCD中,设底面边长为2,侧棱长为3.
(2)求棱锥的表面积.
棱锥有四个侧面,是全等的等腰三角形,一个底面,为正方形.
例.在正四棱锥P-ABCD中,设底面边长为2,侧棱长为3.
(2)求棱锥的表面积.
例.如果一个棱锥侧面是全等的等腰三角形,它一定是正棱锥吗?试着说明理由.
例.如果一个棱锥侧面是全等的等腰三角形,它一定是正棱锥吗?试着说明理由.
不一定.我们来看下面的反例.
2
2
2
2
1
1
棱台的定义
用平行于棱锥底面的平面去截棱锥,所得截面与底面间的多面体称为棱台.
棱台的定义
原棱锥的底面与截面分别称为棱台的下底面与上底面,
其余各面称为棱台的侧面,
相邻两侧面的公共边称为棱台的侧棱.
棱台的定义
上底面
下底面
侧面
侧棱
棱台的定义
棱台的特征
①由棱锥截得
②底面为多边形
③底面平行
④侧面为梯形
注意:棱台必须能还原成棱锥,左图不是棱台
棱台的定义
过棱台一个底面上的任意一个顶点,作另一个底面的垂线所得到的线段称为棱台的高.
棱台的分类
棱台也可以分为三棱台,四棱台,……
由正棱锥截得的棱台称为正棱台.
正棱台的侧面都是全等的等腰梯形,这些等腰梯形的高都相等,称作正棱台的斜高.
例.在正三棱台A'B'C'-ABC中,上底面边长和侧棱都为1,下底面边长为2.
(1)求棱台的斜高;
(2)求棱台的高.
例.在正三棱台A'B'C'-ABC中,上底面边长和侧棱都为1,下底面边长为2.
(1)在侧面的梯形ACC'A'中,
作A'E,C'F垂直于AC,
由AC=2,A'C'=1可知AE=CF=
,
又AA'=1,从而A'E=
,
即斜高为
E
F
例.在正三棱台A'B'C'-ABC中,上底面边长和侧棱都为1,下底面边长为2.
(2)将正三棱台还原为正三棱锥
P-ABC,连接P和底面中心O,则OP与面A'B'C'的交点恰为上底面中心O'
P
O'
O
例.在正三棱台A'B'C'-ABC中,上底面边长和侧棱都为1,下底面边长为2.
(2)在等边三角形ABC中,由于
AB=2,可以计算出OC=
同理O'C'=
P
O'
O
例.在正三棱台A'B'C'-ABC中,上底面边长和侧棱都为1,下底面边长为2.
只看等边三角形ABC,由于
AB=2,所以CD=1,又
在三角形COD中,
E
例.在正三棱台A'B'C'-ABC中,上底面边长和侧棱都为1,下底面边长为2.
OC=
,同理O'C'=
,
在三角形POC中,O'C'为中位线,
于是PC=2CC'=2
P
O'
O
例.在正三棱台A'B'C'-ABC中,上底面边长和侧棱都为1,下底面边长为2.
所以高为
P
O'
O
棱柱棱锥棱台的特征
棱柱
棱锥
棱台
①底面平行
②侧面是平行四边形
③顶点在底面上
①底面为多边形
②侧面为三角形
③侧面共顶点
①由棱锥截得
②底面为多边形
③底面平行
④侧面为梯形
我们一般是从点、线、面这些基本元素入手,用它们的形状、大小与位置关系去刻画几何体的结构特征.
例如形状:底面多边形,侧面三角形,……
位置关系:底面平行,侧面共顶点,……
棱柱棱锥棱台的特征
让我们再想一想,我们在这两节课的学习中,都碰到了哪些点线面之间的位置关系?
棱柱棱锥棱台的特征
平面与平面平行:棱柱或棱台的两个底面
平面与平面相交:棱锥的各个侧面
棱柱棱锥棱台的特征
直线与平面平行:棱柱或棱台一个底面中的边与另一个底面
直线与平面相交:侧棱与底面
直线在平面内:侧棱在侧面内
棱柱棱锥棱台的特征
直线与直线平行,直线与直线相交,直线与直线异面,同学们可以课下自己找一找.
棱柱棱锥棱台的特征
棱柱棱锥棱台的分类
棱柱
棱锥
棱台
斜棱柱
直棱柱
正棱锥
……
正棱台
……
……
正棱柱
……
小
结
一、棱锥的定义,顶点,底面,侧面,侧棱
二、棱台的定义,底面,侧面,侧棱
三、棱柱、棱锥、棱台的特征与分类对比
作
业
课本75页练习A
2,3,4,5
谢谢聆听!
