人教B版(2019)必修(第四册)第十一章 立体几何初步11.1 空间几何体11.1.5圆柱圆锥圆台球(28张PPT)
文档属性
| 名称 | 人教B版(2019)必修(第四册)第十一章 立体几何初步11.1 空间几何体11.1.5圆柱圆锥圆台球(28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 12.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-20 00:00:00 | ||
图片预览








文档简介
(共28张PPT)
高一年级
数学
圆柱圆锥圆台球
观察这些空间图形,你有什么发现呢?
几何抽象
一、旋转体及相关概念;
二、简单旋转体的相关概念及性质;
三、简单旋转体的表面积计算.
旋转体知识概要
一、旋转体及相关概念
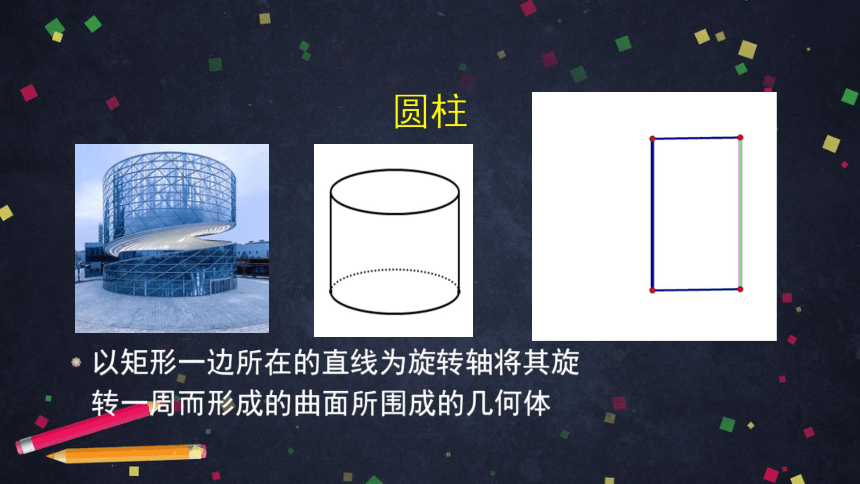
圆柱
以矩形一边所在的直线为旋转轴将其旋转一周而形成的曲面所围成的几何体
圆锥
以直角三角形一直角边所在的直线为旋转轴将其旋转一周而形成的曲面所围成的几何体
圆台
以直角梯形垂直于底边的腰所在的直线为旋转轴将其旋转一周而形成的曲面所围成的几何体
亦可看成平行于圆锥底面的平面截圆锥所得的几何体
旋转体及相关概念
旋转体:用类似形成圆柱圆锥圆台的方式构成的几何体
旋转体的轴、高:旋转轴,轴上的边(或它的长度)
旋转体的底面:垂直于轴的边旋转而成的圆面
旋转体的侧面:不垂直于轴的边旋转而成的曲面
旋转体的母线:不垂直于轴的边
旋转体的轴截面:通过轴的平面所得到的截面
球
一个半圆绕它直径所在的直线旋转一周形成球面,球面围成的几何体称为球
画法(正等测(课下自查))
平行依旧垂改斜
横等纵半竖不变
眼前实线遮为虚
二、简单旋转体的
相关概念及性质
圆柱相关概念及性质
连心线垂直于圆柱底面
平行于底面的截面是与底面全等的圆
轴截面是一个由上下底面直径和母线组成的矩形
平行于轴的截面是一个由上下底面的弦和母线
组成的矩形
圆锥相关概念及性质
过圆锥顶点的截面都是以母线为腰底面弦为底的
等腰三角形,轴截面面积不一定最大
平行于底面的截面面积与底面面积的比等于从顶
点到截面和从顶点到底面距离的平方比
圆锥母线l,高h和底面半径r组成一个直角三角形,
有关系式:
圆台相关概念及性质
圆台的任两条母线延长均可相交,任意两条母
线确定的截面为等腰梯形,在这样的所有截面中,
轴截面面积不一定最大!
与上下底面都相交的截面不一定是梯形!
母线l,高h,上下底面半径r,R之间有:
球相关概念
球心:形成球面的半圆的圆心
半径:连接球面上一点和球心的线段
直径:连接球面上两点且通过球心的线段
表示:可以用它球心的字母来表示,球O
球面:空间中到一个定点距离等于定长的点的集合,
与球是两个概念
球性质
用一个平面α去截球O,所得截面为圆
球的大圆:球面被经过球心的平面截得的圆
球的小圆:被不经过球心的平面截得的圆
球半径为R,截面圆圆心为O1,半径为r,则
三、简单旋转体的表面积
圆柱、圆锥、圆台的面积
三个概念:侧面积、底面积、表面积
球的表面积
球面是不能平面展开的图形
想知道数学史上,先贤们是怎么思考的吗?
现在我们可以这样想:
球面面积肯定只与它的半径R相关且肯定与
成正比!
四、概念、性质运用巩固
简单运用1
例1.把地球看成一个半径为6370km的
球,已知我国首都北京靠近北纬40°.
求北纬40°纬线的长度.
简单运用1
解:设A是北纬40°圈上的一点,K为
北纬40°圈的圆心,O为球心,所以
AK⊥OK,∠AOB=∠OAK=40°,所以
北纬40°纬线的长度为:
简单运用2
例2.已知一个长方体8个顶点都在球面上,且该长方体的棱长分别为3,4,5,求球的表面积
解:由题设可知,长方体的
对角线的中点就是球心,又因
所以所求球的表面积为:
简单运用2
一、圆柱、圆锥、圆台、球的几何结构特征及描述:语言描述(定义、性质),直观描述
数据刻画
二、旋转体及相关概念.
小结
巩固作业
1.通读课本
2.课本P81
练习A,练习B
同学们再见!
高一年级
数学
圆柱圆锥圆台球
观察这些空间图形,你有什么发现呢?
几何抽象
一、旋转体及相关概念;
二、简单旋转体的相关概念及性质;
三、简单旋转体的表面积计算.
旋转体知识概要
一、旋转体及相关概念
圆柱
以矩形一边所在的直线为旋转轴将其旋转一周而形成的曲面所围成的几何体
圆锥
以直角三角形一直角边所在的直线为旋转轴将其旋转一周而形成的曲面所围成的几何体
圆台
以直角梯形垂直于底边的腰所在的直线为旋转轴将其旋转一周而形成的曲面所围成的几何体
亦可看成平行于圆锥底面的平面截圆锥所得的几何体
旋转体及相关概念
旋转体:用类似形成圆柱圆锥圆台的方式构成的几何体
旋转体的轴、高:旋转轴,轴上的边(或它的长度)
旋转体的底面:垂直于轴的边旋转而成的圆面
旋转体的侧面:不垂直于轴的边旋转而成的曲面
旋转体的母线:不垂直于轴的边
旋转体的轴截面:通过轴的平面所得到的截面
球
一个半圆绕它直径所在的直线旋转一周形成球面,球面围成的几何体称为球
画法(正等测(课下自查))
平行依旧垂改斜
横等纵半竖不变
眼前实线遮为虚
二、简单旋转体的
相关概念及性质
圆柱相关概念及性质
连心线垂直于圆柱底面
平行于底面的截面是与底面全等的圆
轴截面是一个由上下底面直径和母线组成的矩形
平行于轴的截面是一个由上下底面的弦和母线
组成的矩形
圆锥相关概念及性质
过圆锥顶点的截面都是以母线为腰底面弦为底的
等腰三角形,轴截面面积不一定最大
平行于底面的截面面积与底面面积的比等于从顶
点到截面和从顶点到底面距离的平方比
圆锥母线l,高h和底面半径r组成一个直角三角形,
有关系式:
圆台相关概念及性质
圆台的任两条母线延长均可相交,任意两条母
线确定的截面为等腰梯形,在这样的所有截面中,
轴截面面积不一定最大!
与上下底面都相交的截面不一定是梯形!
母线l,高h,上下底面半径r,R之间有:
球相关概念
球心:形成球面的半圆的圆心
半径:连接球面上一点和球心的线段
直径:连接球面上两点且通过球心的线段
表示:可以用它球心的字母来表示,球O
球面:空间中到一个定点距离等于定长的点的集合,
与球是两个概念
球性质
用一个平面α去截球O,所得截面为圆
球的大圆:球面被经过球心的平面截得的圆
球的小圆:被不经过球心的平面截得的圆
球半径为R,截面圆圆心为O1,半径为r,则
三、简单旋转体的表面积
圆柱、圆锥、圆台的面积
三个概念:侧面积、底面积、表面积
球的表面积
球面是不能平面展开的图形
想知道数学史上,先贤们是怎么思考的吗?
现在我们可以这样想:
球面面积肯定只与它的半径R相关且肯定与
成正比!
四、概念、性质运用巩固
简单运用1
例1.把地球看成一个半径为6370km的
球,已知我国首都北京靠近北纬40°.
求北纬40°纬线的长度.
简单运用1
解:设A是北纬40°圈上的一点,K为
北纬40°圈的圆心,O为球心,所以
AK⊥OK,∠AOB=∠OAK=40°,所以
北纬40°纬线的长度为:
简单运用2
例2.已知一个长方体8个顶点都在球面上,且该长方体的棱长分别为3,4,5,求球的表面积
解:由题设可知,长方体的
对角线的中点就是球心,又因
所以所求球的表面积为:
简单运用2
一、圆柱、圆锥、圆台、球的几何结构特征及描述:语言描述(定义、性质),直观描述
数据刻画
二、旋转体及相关概念.
小结
巩固作业
1.通读课本
2.课本P81
练习A,练习B
同学们再见!
