沪科版八年级下册数学19.3.1 矩形的性质课件 (共18张PPT)
文档属性
| 名称 | 沪科版八年级下册数学19.3.1 矩形的性质课件 (共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-18 00:00:00 | ||
图片预览


文档简介
(共18张PPT)
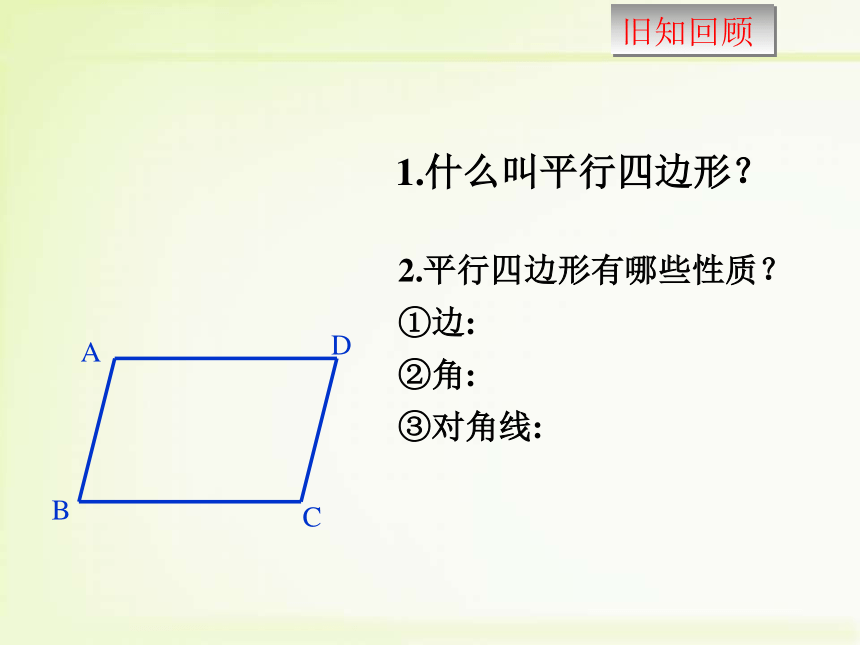
1.什么叫平行四边形?
2.平行四边形有哪些性质?
①边:
②角:
③对角线:
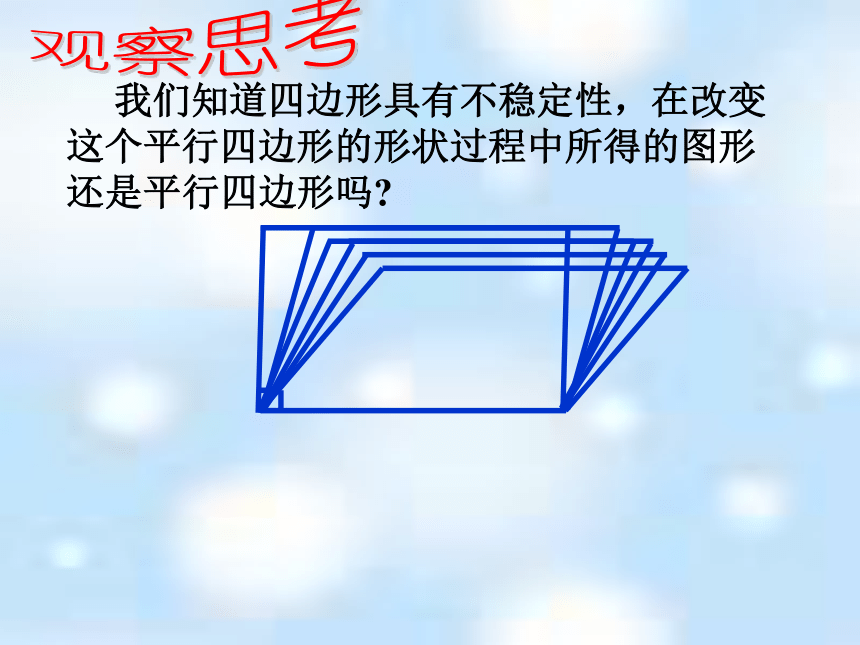
我们知道四边形具有不稳定性,在改变
这个平行四边形的形状过程中所得的图形
还是平行四边形吗?
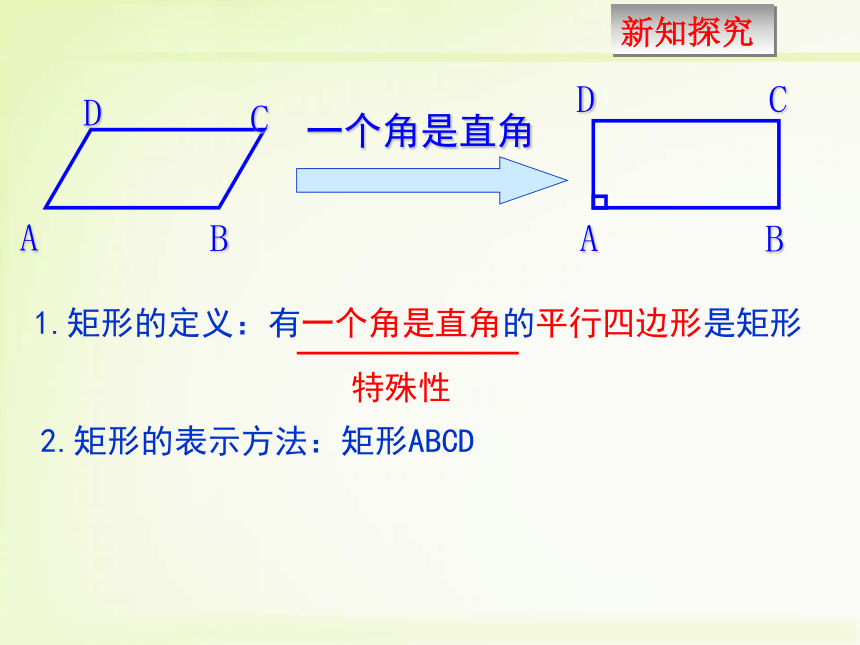
1.矩形的定义:有一个角是直角的平行四边形是矩形
一个角是直角
2.矩形的表示方法:矩形ABCD
(1)
矩形是不是平行四边形?
(2)
平行四边形是不是矩形?
实质上:矩形是特殊的平行四边形。
议一议
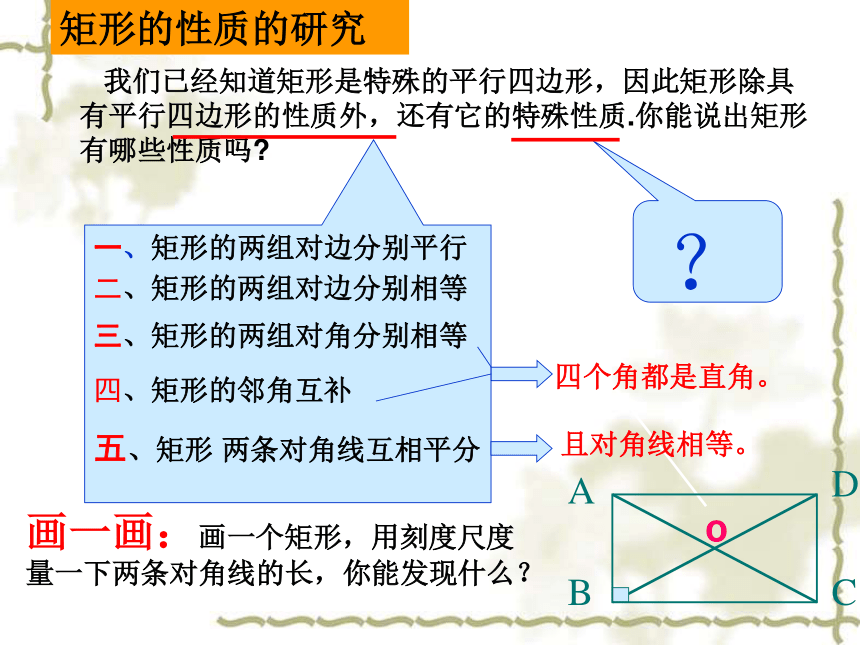
矩形的性质的研究
我们已经知道矩形是特殊的平行四边形,因此矩形除具有平行四边形的性质外,还有它的特殊性质.你能说出矩形有哪些性质吗?
E
。
五、矩形
两条对角线互相平分
三、矩形的两组对角分别相等
二、矩形的两组对边分别相等
一、矩形的两组对边分别平行
四、矩形的邻角互补
?
四个角都是直角。
且对角线相等。
A
B
C
D
画一画:画一个矩形,用刻度尺度量一下两条对角线的长,你能发现什么?
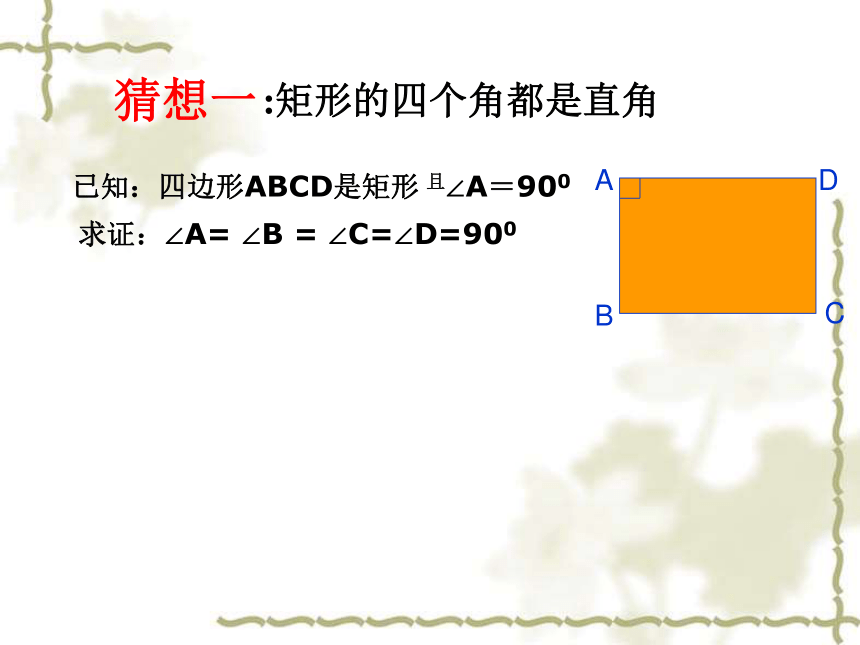
已知:四边形ABCD是矩形
且∠A=900
求证:∠A=
∠B
=
∠C=∠D=900
:矩形的四个角都是直角
猜想一
矩形的性质定理1:
矩形的四个角都是直角
符号语言:
∵四边形ABCD是矩形
∴∠A=∠B=∠C=∠D=900
已知:如图,四边形ABCD是矩形
求证:AC
=
BD
证明:在矩形ABCD中
∵∠ABC
=
∠DCB
=
90°
又∵AB
=
DC
,
BC
=
CB
∴△ABC≌△DCB
∴AC
=
BD
即矩形的对角线相等
:矩形的对角线相等
猜想二
:矩形的对角线相等
∵四边形ABCD是矩形
∴AC
=
BD
矩形的性质定理2
符号语言:
O
A
B
C
D
公平,因为OA=OC=OB=OD
A
B
C
O
推论:直角三角形斜边上的中线等于斜边的一半.(逆命题也成立)
在Rt△ABC中,
BO=
AC
探索新知
在直角三角形ABC中,O是AC中点,思考BO与AC的数量关系
O
D
例1:
如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4㎝,求矩形对角线的长?
1.矩形具有而一般平行四边形不具有的性质是(
).
A
对角线相等
B
对边相等
A
C
对角相等
D
对角线互相平分
选一选
2.矩形ABCD中,已知AB=8㎝,AD=6㎝,
则OB=____
㎝,若已知∠CAB=40°,
则
∠OBA=____
∠AOD=____
5
40°
80°
40°
填一填
练习:如图,BE、CF分别是△ABC的高,M为BC的中点,EF=5,BC=8,求△EFM的周长.
本题考查的是矩形性质的推论,抓住推论成立的两个条件((1)直角三角形(2)斜边上的中线)是解本类题的关键.
四个角都是直
角
对边平行且相
等
对角线互相平
分且相等
课堂小结:通过本节课的学习你有哪些收获?
1.矩形的定义。
2.矩形的性质。
3.推论:直角三角形斜边上的中线等于斜边的一半
必做题:
1.《同步练习》19.3
基础练习一
2.预习“矩形的判定”,你能找到几种判定矩形的方法?
选做题:
矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形周长的和是68cm,对角线长为10cm,求矩形的周长.
1.什么叫平行四边形?
2.平行四边形有哪些性质?
①边:
②角:
③对角线:
我们知道四边形具有不稳定性,在改变
这个平行四边形的形状过程中所得的图形
还是平行四边形吗?
1.矩形的定义:有一个角是直角的平行四边形是矩形
一个角是直角
2.矩形的表示方法:矩形ABCD
(1)
矩形是不是平行四边形?
(2)
平行四边形是不是矩形?
实质上:矩形是特殊的平行四边形。
议一议
矩形的性质的研究
我们已经知道矩形是特殊的平行四边形,因此矩形除具有平行四边形的性质外,还有它的特殊性质.你能说出矩形有哪些性质吗?
E
。
五、矩形
两条对角线互相平分
三、矩形的两组对角分别相等
二、矩形的两组对边分别相等
一、矩形的两组对边分别平行
四、矩形的邻角互补
?
四个角都是直角。
且对角线相等。
A
B
C
D
画一画:画一个矩形,用刻度尺度量一下两条对角线的长,你能发现什么?
已知:四边形ABCD是矩形
且∠A=900
求证:∠A=
∠B
=
∠C=∠D=900
:矩形的四个角都是直角
猜想一
矩形的性质定理1:
矩形的四个角都是直角
符号语言:
∵四边形ABCD是矩形
∴∠A=∠B=∠C=∠D=900
已知:如图,四边形ABCD是矩形
求证:AC
=
BD
证明:在矩形ABCD中
∵∠ABC
=
∠DCB
=
90°
又∵AB
=
DC
,
BC
=
CB
∴△ABC≌△DCB
∴AC
=
BD
即矩形的对角线相等
:矩形的对角线相等
猜想二
:矩形的对角线相等
∵四边形ABCD是矩形
∴AC
=
BD
矩形的性质定理2
符号语言:
O
A
B
C
D
公平,因为OA=OC=OB=OD
A
B
C
O
推论:直角三角形斜边上的中线等于斜边的一半.(逆命题也成立)
在Rt△ABC中,
BO=
AC
探索新知
在直角三角形ABC中,O是AC中点,思考BO与AC的数量关系
O
D
例1:
如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4㎝,求矩形对角线的长?
1.矩形具有而一般平行四边形不具有的性质是(
).
A
对角线相等
B
对边相等
A
C
对角相等
D
对角线互相平分
选一选
2.矩形ABCD中,已知AB=8㎝,AD=6㎝,
则OB=____
㎝,若已知∠CAB=40°,
则
∠OBA=____
∠AOD=____
5
40°
80°
40°
填一填
练习:如图,BE、CF分别是△ABC的高,M为BC的中点,EF=5,BC=8,求△EFM的周长.
本题考查的是矩形性质的推论,抓住推论成立的两个条件((1)直角三角形(2)斜边上的中线)是解本类题的关键.
四个角都是直
角
对边平行且相
等
对角线互相平
分且相等
课堂小结:通过本节课的学习你有哪些收获?
1.矩形的定义。
2.矩形的性质。
3.推论:直角三角形斜边上的中线等于斜边的一半
必做题:
1.《同步练习》19.3
基础练习一
2.预习“矩形的判定”,你能找到几种判定矩形的方法?
选做题:
矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形周长的和是68cm,对角线长为10cm,求矩形的周长.
