西师版数学六年级上册:第二单元 圆 课件(共144张PPT)
文档属性
| 名称 | 西师版数学六年级上册:第二单元 圆 课件(共144张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 12.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-18 20:22:41 | ||
图片预览









文档简介
(共144张PPT)
第 1 课时 圆 的 认 识(1)
第 二 单元 圆
生活中的“圆”
生活中的“圆”
圆是平面曲线图形。
1.自学例题,把重点字词画一画。
2.用学具圆折一折、画一画并用深色水彩笔
标出圆心、半径和直径。
相信你 能做到
o
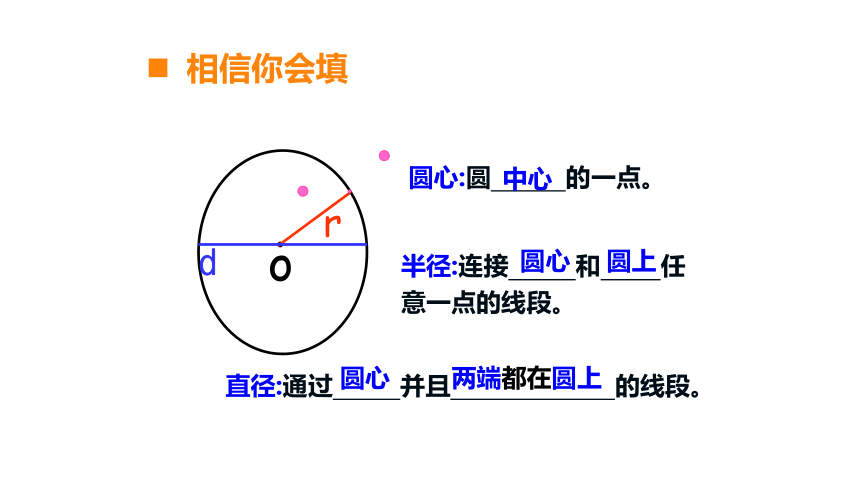
圆心:圆 的一点。
半径:连接 和 任意一点的线段。
r
d
直径:通过 并且 的线段。
中心
圆心
圆上
圆心
两端都在圆上
相信你会填
o
A
C
B
D
E
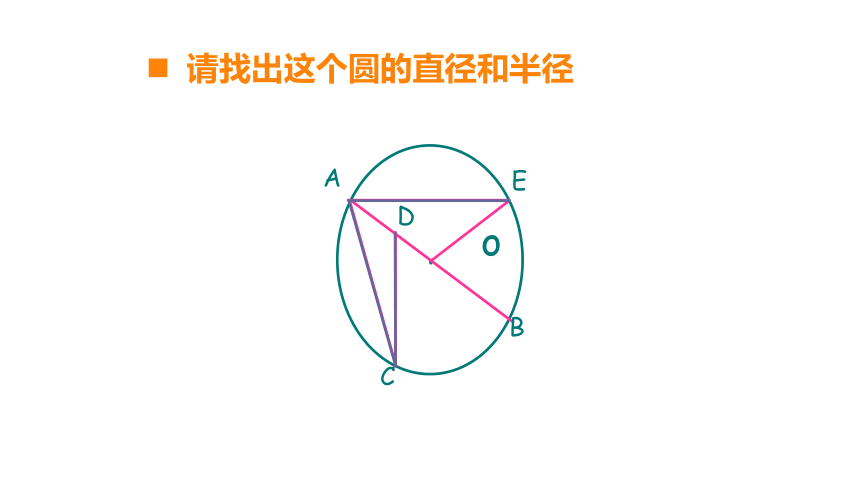
请找出这个圆的直径和半径
汇报单
1.同圆内,有( )条半径,长度都( )。
2.同圆内,有( )条直径,长度都( )。
3.同圆内,直径和半径的长度有什么关系?
答:____________________________
____________________________
在小组里说说你们是用什么方法验证的。
四人小组合作, 用学具圆画一画、量一量、比一比,把你们的结论写在汇报单上,并在小组里说说你们是用什么方法验证的。
合作探究
1.所有圆的直径都相等。( )
2.两端都在圆上的线段叫做直径。( )
3.在同一圆内,只可以画100条半径。( )
4.一个圆的直径长度是10cm,它的半径
长度是5cm。( )
√
×
×
×
判断
墨子
著名思想家墨子在他的著作《墨经》中这样描述:“圆,一中同长也”。这一发现在当初要比西方整整早了1000多年 。
在操场上要画一个半径为5m的圆,有什么办法 ?
思考
第 2 课时 圆 的 认 识(2)
第 二 单元 圆
复习
一、判断正误
(1)所有的圆的直径都相等。( )
(2)等圆的半径都相等。 ( )
(3)圆心到圆上任意一点的距离都相等。( )
(4)半径是2cm的圆比直径是3cm的圆大。
( )
√
×
√
√
复习
二、用圆规画一个半径是3cm的圆,并用字母o、r、d标出它的圆心、半径和直径。
复习
三、我们以前学过哪些对称图形,它们的对称轴各是什么?
动手试一试
请你拿出两个大小不同的学具圆,你能分别找出它们的对称轴吗?你能找到几条?你发现了什么?
课堂练习
在下列各图形中,你能分别画出几条对称轴?
动手试一试
请你在练习本上画一个只有一条对称轴的四边形;再画一个只有2条对称轴的四边形。
第 3 课时 圆 的 周 长(1)
第 二 单元 圆
1km
1km
熊大绕着直径为1km的圆跑一圈,而熊二绕着边长为1km的正方形跑一圈。
熊大熊二赛跑
认识圆的周长
1km
1km
正方形的周长
圆的周长
C正方形= 4a
= 4×1
= 4 (km)
C圆
熊大熊二赛跑
认识圆的周长
围成圆的曲线的长叫做圆的周长。
什么是圆的周长?
认识圆的周长
化曲为直
绕线法
滚动法
怎样测出圆的周长呢?
圆的周长的测量
方法一:绕线法
圆的周长的测量
方法一:绕线法
圆的周长的测量
方法一:绕线法
圆的周长的测量
方法一:绕线法
圆的周长的测量
方法一:绕线法
圆的周长的测量
0
1
2
3
4
方法一:绕线法
圆的周长的测量
0
1
3
方法二:滚动法
2
4
圆的周长的测量
0
1
2
3
4
圆的周长的测量
方法二:滚动法
0
1
2
3
4
圆的周长的测量
方法二:滚动法
0
1
2
3
4
圆的周长的测量
方法二:滚动法
0
1
2
3
4
圆的周长的测量
方法二:滚动法
0
1
2
3
4
圆的周长的测量
方法二:滚动法
0
1
2
3
4
圆的周长的测量
方法二:滚动法
0
1
2
3
4
圆的周长的测量
方法二:滚动法
0
1
2
3
4
圆的周长的测量
方法二:滚动法
圆的周长与什么有关呢?
圆的周长与直径(半径)有关。
直径(半径)越长,圆周长就越大。
圆的周长的计算
探索圆周长与直径的关系
找几个大小不同的圆形物品,量出圆的直径和周长。
1元硬币
圆周长
直 径
圆周长除以直径的商(保留两位小数)
自主探究
圆的周长除以直径的商是一个固定的数,
我们把它叫做圆周率,用字母π表示。
π =3.141592653…
π是一个无限不循环小数。
π≈3.14
圆的周长的测量
圆的周长总是直径的 倍多一些。
3
我发现:
圆的周长的测量
C=
d
π
或
C=
r
2 π
固定值
圆的周长是直径的π倍。
圆的周长的测量
约2000年前,中国的古代数学著作《周髀算经》中就有了“周三径一”的说法,意思是指圆的周长是它的直径的三倍。
知识拓展
祖冲之的故事
大约1500年前,中国有一位伟大的数学家和天文学家祖冲之,他计算出圆周率应在3.1415926和3.1415927之间,成为世界上第一个把圆周率的值精确到7位小数的人。他的这项伟大成就比国数学家得出这样精确数值的时间,至少要早1000年。为了纪念他,科学家把月球上的一座环形山命名为祖冲之山,这是我们中华民族的骄傲。
知识拓展
2
自行车车轮的外直径是0.71m。车轮转1 周,自行车前进多少米?(得数保留两位小数)
3.14×0.71
=
≈
答:自行车约前进2.23 m。
2.2294
2.23(m)
1.求下面各圆的周长。
d=4厘米
r=1.5米
3.14×4=12.56(cm)
3.14×1.5×2=9.42(m)
智慧岛
1. 钟面分针长10cm,它旋转一周针尖走过多少厘米?
3. 一张圆桌面的直径是0.95m,求它的周长是多少米?(得数保留两位小数)
2. 花瓶最大处的半径是15cm,求这一周的长度是多少厘米?
智慧岛
2×10×3.14=62.8(厘米)
2×15×3.14=94.2(厘米)
0.95×3.14=2.98(米)
小丽量得一个古代建筑中的大圆柱的周长是4.52m。这个圆柱的直径是多少米?(得数保留一位小数)
智慧岛
4.52÷3.14=1.4(米)
小明的妈妈在自家的墙根下建了一个花坛(如图)。你能计算出花坛的周长吗?
8米
智慧岛
下图是育才小学操场的跑道,跑道外圈长多少米?内圈长多少米?(两端各是半圆)
100m
10m
3m
智慧岛
内圈长:2×100+2×10×3.14=262.8(米)
外圈长:2×100+2×13×3.14=281.64(米)
第 4 课时 圆 的 周 长(2)
第 二 单元 圆
填一填
(1)圆周率是( )和( )的比值,它用字母( )表示,它是我国古代数学家( )发现的。
周长
直径
祖冲之
(2)圆的周长总是直径的( )倍。已知圆的直径就可以用公式( )求周长;已知圆的半径就可以用公式( )求周长。
π
C=
d
π
C=
r
2π
π
(1)只要知道圆的直径或半径就可以计算出圆的周长。
(2)大圆的圆周率大,小圆的圆周率小。
(3)π的值就是3.14。
(4)直径是半径的2倍。
(5)半圆的周长是圆周长的一半。
(√)
(×)
(×)
(×)
(×)
判断
算一算
求下列各圆的周长。
C=2πr
3.14×2×2
=12.56(cm)
C=πd
3.14×5
=15.7(m)
C=2πr
3.14×2×1.5
=9.42(dm)
解决问题
一个圆形跑道的半径是5m,它的周长是多少米?小明跑了3圈,小明跑了多少米?
5×2×3.14=31.4(m)
31.4×3=94.2(m)
答:小明跑了94.2m。
解决问题
这个水池的直径和半径分别是多少米?
水池的周长是31.4m。
解决问题
解:设水池的直径是dm。根据C=πd得
3.14d=31.4
d=10
r=10÷2=5
先求出水池的直径,再求出半径。
还能怎样算?
答:这个水池的直径是10m,半径是5m。
练习
4. 在一棵大树的1.2m高处,量出树干的周长。
周长是1.57米。
直径是多少米?
1.57÷3.14=0.5(m)
练习
5. 国庆节活动中,要做一批铁环。如果每个铁环用1.5m长的铁条做成,那么铁环的直径是多少米?(得数保留一位小数)
1.5÷3.14≈0.5(m)
答:铁环的直径是0.5m。
练习
6. 杂技演员表演独轮车走钢丝,车轮直径是0.6m。走过47.1m的钢丝,车轮要转动多少周?
47.1÷(3.14×0.6)=25(圈)
答:车轮要转动25周。
练习
7. 在花卉博览会上,把一个直径为10m的圆形展区的半径向外延伸2m变成一个新的圆形展区。那么这个新展区的周长是多少米?
(10+2+2)×3.14=43.96(米)
答:这个新展区的周长是43.96米。
两只蜜蜂分别沿着涂色部分的边缘爬1次,哪只蜜蜂爬过的路线长?(两个正方形的边长相等。)
思考题
第 5 课时 圆 的 面 积(1)
第 二 单元 圆
云南景洪的曼飞
龙白塔的塔基为
圆柱形石座,底面周长是42.6 m。
这座塔的塔基占
地多少平方米?
以正方形的边长为半径画一个圆,圆面积是正方形面积的几倍?
圆面积比正方形面积的3 倍多一些,也就是比半径平方( r2)的3 倍多一些。
把一个圆分成若干等份后,像下面这样拼接。
分成4份
分成4份
分成8份
分成8份
分成16份
分成16份
1、观察你拼成的图形,和同桌说一说:
平行四边形的底是圆的( )
平行四边形的高是圆的( )
把圆等分的份数越
多,拼出的图形越接
近于平行四边形。
分成16份
周长的一半
半径
长
宽
=
圆周长的一半
=
半径
......
4份
8份
圆形
16份
32份
平行四边形
r
平行四边形面积 = 长 × 宽
圆的面积 = 周长一半 × 半径
r
S = πr2
= × r
2πr
2
S = × r
C
2
=πr×r
1
1
=πr2
议一议 :这个平行四边形与圆之间有什么关系?
量得一张圆桌的周长是3.14m。这张圆桌的面积是多少平方米?
试一试:你能解决第19页上“塔基占地多少平方米”这个问题吗?
求圆的面积,要知
道什么?
r=3.14÷3.14÷2=0.5(m)
S=0.5×0.5×3.14=0.785(平方米)
答:这张圆桌的面积是0.785平方米。
修建一个半径是30m的圆形鱼池,它的占地面积是多少平方米?
3.14×302
= 3.14×900
= 2826(m2)
答:它的占地面积是2826m2。
北京天坛公园的祈年殿是底部直径约24m的圆形大殿。它的占地面积是多少平方米?环绕祈年殿的回音壁是一道圆形的水磨砖围墙,它内圆的半径是32.5m。回音壁内圆的周长是多少米?π取3。
面积:
(24÷2) ×3=432(平方米)
周长:
32.5×2×3=195(米)
答:回音壁内圆的周长是195米。
量得一张圆桌的周长是3.14m。这张圆桌的面积是多少平方米?
试一试:你能解决第19页上“塔基占地多少平方米”这个问题吗?
求圆的面积,要知
道什么?
r=3.14÷3.14÷2=0.5(m)
S=0.5×0.5×3.14=0.785(平方米)
答:这张圆桌的面积是0.785平方米。
用两根长度都是31.4cm的铁丝,分别围出一个正方形和圆。计算出它们的面积。
(3.14÷4) ≈0.62(平方米)
(3.14÷3.14÷2) ×3.14=0.785(平方米)
1. 量出有关数据,并求出圆的面积。
2. 找一个圆形物品,量出圆的直径或周长,再算出面积。
3. 议一议,怎样在一张正方形纸上画出一个最大的圆?动手试一试。
课堂活动
今天我学习了圆的面积。我知道了把一个圆平均分成若干等分,然后拼在一起,可以拼成一个近似( )。长方形的宽是圆的( ),长是圆的( ),求圆面积用公式表示( )。
长方形
周长一半
S=πr 2
半径
r
C
2
=
πr
我的收获
第 6 课时 圆 的 面 积(2)
第 二 单元 圆
1. 公园草地上的自动旋转喷水器的射程是8m。它能喷洒的面积是多少平方米?
S=8×8×3.14=200.96(平方米)
答:它能喷洒的面积是200.96平方米。
2. 一个圆形水缸口的外直径为1m。现在为这个水缸做一个盖子,这个盖子的面积至少是多少平方米?
S=(1÷2) ×3.14=0.785(平方米)
答:这个盖子的面积至少是0.785平方米。
半径(cm) 直径(cm) 周长(cm) 面积(cm2)
10
4
56.52
3.填空
5
31.4
78.5
9
8
25.12
50.24
18
254.34
4. 用下面这张长方形纸剪出一个最大的圆。
圆的直径是多少?
圆的面积是多少?
20cm
14cm
直径为14cm 面积:7×7×3.14=153.86(平方厘米)
张家村修了一个周长是251.2m的圆形蓄水池。它的占地面积是多少平方米?
它的半径:
251.2÷3.14÷2=40(米)
它的面积:
40×40×3.14
=5024(平方米)
答:它的占地面积是5024平方米。
8. 求下图中阴影部分的面积。(图中单位:cm)
6×6×3.14-2×2×3.14=100.46(cm )
10×10-5×5×3.14=21.5(cm )
把一个圆分成若干等份后,拼成近似的梯形或三角形,可以推算出圆面积计算公式吗?
3×3=9(c㎡)
5×3=15(c㎡)
6×3÷2=9(c㎡)
正方形面积=边长×边长
长方形面积=长×宽
三角形面积=底×高÷2
3cm
3cm
3cm
5cm
3cm
6cm
计算下面各图形的面积
3×4
=12(c㎡)
(6+4) ×3÷2
=15(c㎡)
3.14 ×32
=28.26(c㎡)
平行四边形的面积=底×高
圆的面积= 圆周率×半径的平方
梯形的面积=(上底+下底)×高÷2
3cm
3cm
3cm
4cm
4cm
6cm
计算下面各图形的面积
学校阅览室的窗户上面是半圆,下面是正方形。(如下图)窗户的面积约是多少平方米?
学校阅览室的窗户上面是半圆,下面是正方形。(如下图)窗户的面积约是多少平方米?
学校阅览室的窗户上面是半圆,下面是正方形。(如下图)窗户的面积约是多少平方米?
课堂活动
从正方形里截去一个最大的圆。
阴影部分的面积=正方形面积-圆的面积
3个图中的的阴影部分面积相等
1.议一议
涂色部分面积
=半圆形面积-小圆面积
2m
2m
6m
涂色部分面积
=长方形面积+圆面积
10cm
6cm
涂色部分面积
=外圆面积-内圆面积
涂色部分面积
=4个扇形面积之和
=一个圆面积
4.旋转餐厅的直径为36m,旋转部分宽7m。旋转部分的面积是多少平方米?
(36÷2) ×3.14-(36÷2-7) ×3.14=637.42(平方米)
3cm
3cm
课后拓展
求阴影部分的面积?
阴影部分的面积=(四分之一圆-三角形面积)×2
S=(3×3×3.14÷4-
3×3÷2)×2
=5.13(cm )
第 7 课时 组合图形的面积
第 二 单元 圆
一张可折叠的圆桌,半径是0.6m,折叠后成了正方形。折叠部分的面积约是多少平方米?(得数保留两位小数)
折叠部分面积=圆的面积-正方形面积
求圆形花坛周围小路的面积:
课堂活动
课堂活动
o
8m
10m
花坛周围小路的面积 = 外圆面积 - 内半圆面积
课堂活动
花坛外圆的面积:3.14×(8+2)2 =314(㎡)
花坛内圆的面积:3.14 ×82 =200.96 (㎡)
花坛小路的面积:314-200.96=113.04(㎡)
答:花坛周围的小路的面积是113.04 ㎡。
求图中阴影部分的面积。
4×4×3.14=50.24(cm )
一座雕塑的基座是圆形,半径为1.5m,在它的周围植上5m宽的环形草坪(如右图)。
(1)草坪的面积是多少平方米?
(2)如果植1m2草坪的成本为20元,那么植这块草坪的成本至少是多少元?
1.5m
5m
(1)(1.5+5) ÷3.14-1.5×1.5×3.14=125.6(m )
(2)125.6×20=2512(元)
用15.7m长的竹篱笆靠墙围一个半圆型鸡舍(如右图)。这个鸡舍的面积是多少平方米?
注意:15.7=πr≠2πr
第8课时 综合训练
第 二 单元 圆
画一画,算一算
1.画一个边长3cm的圆,用字母标出圆心、半径、直径,再画一条对称轴,计算出它的周长和面积。
2.用圆规设计一副美丽的图案。
两只小蚂蚁从a点出发到b点去取食物,它们选选择了两条不同的路线,谁选择的路线比较短?
求阴影部分的面积
阴影部分的面积=(四分之一圆-三角形面积)×2
S=(8×8×3.14÷4-
8×8÷2)×2
=36.48(cm )
求阴影部分的面积
阴影部分的面积=(四分之一圆-三角形面积)×8
S=(4×4×3.14÷4-
4×4÷2)×8
=36.48(cm )
求阴影部分的面积
两个半圆的面积相等,将其平移过来后,阴影部分的面积就是整个长方形面积的一半。 S=2×1÷2=1(m )
求阴影部分的面积
S=10×10×3.14÷4-
5×5×3.14÷2
=78.5-39.25
=39.25(cm )
下图中,阴影部分的面积是40cm2,求环形面积。
解决问题
R
r
阴影部分的面积=R -r
圆环的面积=R π-r π
=40×3.14
=125.6(cm )
游乐园的圆形高空转椅的直径是10m,如果每隔3.14m装一个吊篮,能装多少个吊篮?
解决问题
10×3.14÷3.14+1=11(个)
圆的认识
圆心
半径
直径
圆的周长
圆的面积
圆
圆周长、面积的拓展
圆形图案的设计制作
1.圆是一个什么样的图形?
圆是由一条曲线围成的封闭图形。属于平面图形中的一种。
圆的认识
圆的认识
2. 什么叫圆心?怎样确定一个圆的圆心?
o
圆心确定圆的位置。
圆的认识
3.什么是圆的半径、直径,在同圆或等圆中,它们有什么关系?
o
r
d
d=2r
半径(或直径)决定圆的大小。
r=d÷2
圆的周长
C=πd
C=2πr
C÷d=π
d=C÷π
圆周率表示什么?是一个什么样的小数?不同圆的圆周率一样吗?
圆的面积
4.什么叫圆的面积?怎么推导出圆面积计算的公式?
圆所占平面的大小叫做圆的面积。
圆的面积
将圆分成若干等分。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
1
2
3
4
5
6
7
8
16
15
14
13
12
11
10
9
将圆分成若干等分。
圆的面积
分的份数越多,拼成的图形越接近长方形。
r
C
2
圆的面积
r
C
2
=
πr
πr × r
S = πr 2
圆的面积 =
知道直径或者周长,怎么求面积?
圆的面积
与圆有关的结算公式
知道半径 (r) 知道直径 (d) 知道周长
(C)
求半径(r)
求直径(d)
求周长(C)
求面积(S)
r=d÷2
r=C÷π÷2
d=2r
d=C÷π
C=2πr
C=πd
S=πr2
S=π(d÷2)2
S=π(C÷π÷2)2
(1)两个半圆一定能拼成一个圆。 ( )
(2)半径是2厘米的圆,周长和面积相等( )
(3)大圆的圆周率比小圆的圆周率大。 ( )
×
×
×
(4)半圆形纸片的周长就是圆周长的一半。( )
(5)把半径3厘米的圆等分成十六份,拼成一个近似长方形,长方形的周长比圆的周长长。 ( )
×
√
判断
(6)在同一个圆内可以画100条直径。
(7)所有的圆的直径都相等。
(8)等圆的半径都相等。
(9)两端都在圆上的线段叫做直径。
(10)圆心到圆上任意一点的距离都相等。
(11)半径是2cm的圆比直径是3cm的圆大。
( )
( )
( )
( )
√
×
×
×
( )
( )
√
√
判断
(1)圆中心的一点叫做( ),一般用字母( )表示。
(2) 连接圆心和圆上任意一点的线段叫做( ),一般用字母r 表示。
(3) 通过圆心并且两端都在圆上的线段叫做( ),一般用字母d 表示。
(4)一个圆内有( )条直径,( )条半径。并且( )条直径的长等于2 条半径的长。
圆心
O
半径
直径
无数
无数
1
填空
(5)圆是( )图形,有( )条对称轴。
(6) 把圆规的两脚分开,定好两脚间的距离作( )。
(7)圆是平面上的一种( )图形。圆的两条直径的交点是圆的( )。
(8)把一个圆形纸片沿半径平均分成若干等份,拼成一个近似的长方形。则面积( ),周长( )。
轴对称
半径
无数
填空
不变
增加
曲线
圆心
(9)周长相等的圆、正方形和长方形,( )的面积最大。
(10)圆中最长的线段是圆的( )。
(11)把一个直径是10cm的圆剪成两个半圆,则两个半圆周长的和是( )cm。
(12)用圆规画一个周长12.56cm的圆,圆规两脚之间的距离是( )cm,所画圆的面积是( )平方厘米。
圆
直径
51.4
填空
2
12.56
(13)圆的半径扩大3倍,直径扩大( )倍,周长扩大( )倍;面积扩大( )倍。
(14)小铁环直径6dm,大铁环直径8dm。大铁环和小铁环半径的比是( );周长的比是( );面积的比是( )。如果它们滚过相同的路程,则转动的圈数的比是( )。
(15)在一张长60cm,宽40cm的长方形纸上剪一个最大的圆,则圆的面积是( )cm2。
3
3
9
3:4
3:4
9:16
4:3
1256
填空
(1)画圆时,圆规两脚间的距离是( )。
A.半径长度 B.直径长度
(2)从圆心到( )任意一点的线段叫半径。
A.圆心 B.圆外 C.圆上
(3)通过圆心并且两端都在圆上的( )叫直径。
A.直线 B.线段 C.射线
A
C
B
选择
第 1 课时 圆 的 认 识(1)
第 二 单元 圆
生活中的“圆”
生活中的“圆”
圆是平面曲线图形。
1.自学例题,把重点字词画一画。
2.用学具圆折一折、画一画并用深色水彩笔
标出圆心、半径和直径。
相信你 能做到
o
圆心:圆 的一点。
半径:连接 和 任意一点的线段。
r
d
直径:通过 并且 的线段。
中心
圆心
圆上
圆心
两端都在圆上
相信你会填
o
A
C
B
D
E
请找出这个圆的直径和半径
汇报单
1.同圆内,有( )条半径,长度都( )。
2.同圆内,有( )条直径,长度都( )。
3.同圆内,直径和半径的长度有什么关系?
答:____________________________
____________________________
在小组里说说你们是用什么方法验证的。
四人小组合作, 用学具圆画一画、量一量、比一比,把你们的结论写在汇报单上,并在小组里说说你们是用什么方法验证的。
合作探究
1.所有圆的直径都相等。( )
2.两端都在圆上的线段叫做直径。( )
3.在同一圆内,只可以画100条半径。( )
4.一个圆的直径长度是10cm,它的半径
长度是5cm。( )
√
×
×
×
判断
墨子
著名思想家墨子在他的著作《墨经》中这样描述:“圆,一中同长也”。这一发现在当初要比西方整整早了1000多年 。
在操场上要画一个半径为5m的圆,有什么办法 ?
思考
第 2 课时 圆 的 认 识(2)
第 二 单元 圆
复习
一、判断正误
(1)所有的圆的直径都相等。( )
(2)等圆的半径都相等。 ( )
(3)圆心到圆上任意一点的距离都相等。( )
(4)半径是2cm的圆比直径是3cm的圆大。
( )
√
×
√
√
复习
二、用圆规画一个半径是3cm的圆,并用字母o、r、d标出它的圆心、半径和直径。
复习
三、我们以前学过哪些对称图形,它们的对称轴各是什么?
动手试一试
请你拿出两个大小不同的学具圆,你能分别找出它们的对称轴吗?你能找到几条?你发现了什么?
课堂练习
在下列各图形中,你能分别画出几条对称轴?
动手试一试
请你在练习本上画一个只有一条对称轴的四边形;再画一个只有2条对称轴的四边形。
第 3 课时 圆 的 周 长(1)
第 二 单元 圆
1km
1km
熊大绕着直径为1km的圆跑一圈,而熊二绕着边长为1km的正方形跑一圈。
熊大熊二赛跑
认识圆的周长
1km
1km
正方形的周长
圆的周长
C正方形= 4a
= 4×1
= 4 (km)
C圆
熊大熊二赛跑
认识圆的周长
围成圆的曲线的长叫做圆的周长。
什么是圆的周长?
认识圆的周长
化曲为直
绕线法
滚动法
怎样测出圆的周长呢?
圆的周长的测量
方法一:绕线法
圆的周长的测量
方法一:绕线法
圆的周长的测量
方法一:绕线法
圆的周长的测量
方法一:绕线法
圆的周长的测量
方法一:绕线法
圆的周长的测量
0
1
2
3
4
方法一:绕线法
圆的周长的测量
0
1
3
方法二:滚动法
2
4
圆的周长的测量
0
1
2
3
4
圆的周长的测量
方法二:滚动法
0
1
2
3
4
圆的周长的测量
方法二:滚动法
0
1
2
3
4
圆的周长的测量
方法二:滚动法
0
1
2
3
4
圆的周长的测量
方法二:滚动法
0
1
2
3
4
圆的周长的测量
方法二:滚动法
0
1
2
3
4
圆的周长的测量
方法二:滚动法
0
1
2
3
4
圆的周长的测量
方法二:滚动法
0
1
2
3
4
圆的周长的测量
方法二:滚动法
圆的周长与什么有关呢?
圆的周长与直径(半径)有关。
直径(半径)越长,圆周长就越大。
圆的周长的计算
探索圆周长与直径的关系
找几个大小不同的圆形物品,量出圆的直径和周长。
1元硬币
圆周长
直 径
圆周长除以直径的商(保留两位小数)
自主探究
圆的周长除以直径的商是一个固定的数,
我们把它叫做圆周率,用字母π表示。
π =3.141592653…
π是一个无限不循环小数。
π≈3.14
圆的周长的测量
圆的周长总是直径的 倍多一些。
3
我发现:
圆的周长的测量
C=
d
π
或
C=
r
2 π
固定值
圆的周长是直径的π倍。
圆的周长的测量
约2000年前,中国的古代数学著作《周髀算经》中就有了“周三径一”的说法,意思是指圆的周长是它的直径的三倍。
知识拓展
祖冲之的故事
大约1500年前,中国有一位伟大的数学家和天文学家祖冲之,他计算出圆周率应在3.1415926和3.1415927之间,成为世界上第一个把圆周率的值精确到7位小数的人。他的这项伟大成就比国数学家得出这样精确数值的时间,至少要早1000年。为了纪念他,科学家把月球上的一座环形山命名为祖冲之山,这是我们中华民族的骄傲。
知识拓展
2
自行车车轮的外直径是0.71m。车轮转1 周,自行车前进多少米?(得数保留两位小数)
3.14×0.71
=
≈
答:自行车约前进2.23 m。
2.2294
2.23(m)
1.求下面各圆的周长。
d=4厘米
r=1.5米
3.14×4=12.56(cm)
3.14×1.5×2=9.42(m)
智慧岛
1. 钟面分针长10cm,它旋转一周针尖走过多少厘米?
3. 一张圆桌面的直径是0.95m,求它的周长是多少米?(得数保留两位小数)
2. 花瓶最大处的半径是15cm,求这一周的长度是多少厘米?
智慧岛
2×10×3.14=62.8(厘米)
2×15×3.14=94.2(厘米)
0.95×3.14=2.98(米)
小丽量得一个古代建筑中的大圆柱的周长是4.52m。这个圆柱的直径是多少米?(得数保留一位小数)
智慧岛
4.52÷3.14=1.4(米)
小明的妈妈在自家的墙根下建了一个花坛(如图)。你能计算出花坛的周长吗?
8米
智慧岛
下图是育才小学操场的跑道,跑道外圈长多少米?内圈长多少米?(两端各是半圆)
100m
10m
3m
智慧岛
内圈长:2×100+2×10×3.14=262.8(米)
外圈长:2×100+2×13×3.14=281.64(米)
第 4 课时 圆 的 周 长(2)
第 二 单元 圆
填一填
(1)圆周率是( )和( )的比值,它用字母( )表示,它是我国古代数学家( )发现的。
周长
直径
祖冲之
(2)圆的周长总是直径的( )倍。已知圆的直径就可以用公式( )求周长;已知圆的半径就可以用公式( )求周长。
π
C=
d
π
C=
r
2π
π
(1)只要知道圆的直径或半径就可以计算出圆的周长。
(2)大圆的圆周率大,小圆的圆周率小。
(3)π的值就是3.14。
(4)直径是半径的2倍。
(5)半圆的周长是圆周长的一半。
(√)
(×)
(×)
(×)
(×)
判断
算一算
求下列各圆的周长。
C=2πr
3.14×2×2
=12.56(cm)
C=πd
3.14×5
=15.7(m)
C=2πr
3.14×2×1.5
=9.42(dm)
解决问题
一个圆形跑道的半径是5m,它的周长是多少米?小明跑了3圈,小明跑了多少米?
5×2×3.14=31.4(m)
31.4×3=94.2(m)
答:小明跑了94.2m。
解决问题
这个水池的直径和半径分别是多少米?
水池的周长是31.4m。
解决问题
解:设水池的直径是dm。根据C=πd得
3.14d=31.4
d=10
r=10÷2=5
先求出水池的直径,再求出半径。
还能怎样算?
答:这个水池的直径是10m,半径是5m。
练习
4. 在一棵大树的1.2m高处,量出树干的周长。
周长是1.57米。
直径是多少米?
1.57÷3.14=0.5(m)
练习
5. 国庆节活动中,要做一批铁环。如果每个铁环用1.5m长的铁条做成,那么铁环的直径是多少米?(得数保留一位小数)
1.5÷3.14≈0.5(m)
答:铁环的直径是0.5m。
练习
6. 杂技演员表演独轮车走钢丝,车轮直径是0.6m。走过47.1m的钢丝,车轮要转动多少周?
47.1÷(3.14×0.6)=25(圈)
答:车轮要转动25周。
练习
7. 在花卉博览会上,把一个直径为10m的圆形展区的半径向外延伸2m变成一个新的圆形展区。那么这个新展区的周长是多少米?
(10+2+2)×3.14=43.96(米)
答:这个新展区的周长是43.96米。
两只蜜蜂分别沿着涂色部分的边缘爬1次,哪只蜜蜂爬过的路线长?(两个正方形的边长相等。)
思考题
第 5 课时 圆 的 面 积(1)
第 二 单元 圆
云南景洪的曼飞
龙白塔的塔基为
圆柱形石座,底面周长是42.6 m。
这座塔的塔基占
地多少平方米?
以正方形的边长为半径画一个圆,圆面积是正方形面积的几倍?
圆面积比正方形面积的3 倍多一些,也就是比半径平方( r2)的3 倍多一些。
把一个圆分成若干等份后,像下面这样拼接。
分成4份
分成4份
分成8份
分成8份
分成16份
分成16份
1、观察你拼成的图形,和同桌说一说:
平行四边形的底是圆的( )
平行四边形的高是圆的( )
把圆等分的份数越
多,拼出的图形越接
近于平行四边形。
分成16份
周长的一半
半径
长
宽
=
圆周长的一半
=
半径
......
4份
8份
圆形
16份
32份
平行四边形
r
平行四边形面积 = 长 × 宽
圆的面积 = 周长一半 × 半径
r
S = πr2
= × r
2πr
2
S = × r
C
2
=πr×r
1
1
=πr2
议一议 :这个平行四边形与圆之间有什么关系?
量得一张圆桌的周长是3.14m。这张圆桌的面积是多少平方米?
试一试:你能解决第19页上“塔基占地多少平方米”这个问题吗?
求圆的面积,要知
道什么?
r=3.14÷3.14÷2=0.5(m)
S=0.5×0.5×3.14=0.785(平方米)
答:这张圆桌的面积是0.785平方米。
修建一个半径是30m的圆形鱼池,它的占地面积是多少平方米?
3.14×302
= 3.14×900
= 2826(m2)
答:它的占地面积是2826m2。
北京天坛公园的祈年殿是底部直径约24m的圆形大殿。它的占地面积是多少平方米?环绕祈年殿的回音壁是一道圆形的水磨砖围墙,它内圆的半径是32.5m。回音壁内圆的周长是多少米?π取3。
面积:
(24÷2) ×3=432(平方米)
周长:
32.5×2×3=195(米)
答:回音壁内圆的周长是195米。
量得一张圆桌的周长是3.14m。这张圆桌的面积是多少平方米?
试一试:你能解决第19页上“塔基占地多少平方米”这个问题吗?
求圆的面积,要知
道什么?
r=3.14÷3.14÷2=0.5(m)
S=0.5×0.5×3.14=0.785(平方米)
答:这张圆桌的面积是0.785平方米。
用两根长度都是31.4cm的铁丝,分别围出一个正方形和圆。计算出它们的面积。
(3.14÷4) ≈0.62(平方米)
(3.14÷3.14÷2) ×3.14=0.785(平方米)
1. 量出有关数据,并求出圆的面积。
2. 找一个圆形物品,量出圆的直径或周长,再算出面积。
3. 议一议,怎样在一张正方形纸上画出一个最大的圆?动手试一试。
课堂活动
今天我学习了圆的面积。我知道了把一个圆平均分成若干等分,然后拼在一起,可以拼成一个近似( )。长方形的宽是圆的( ),长是圆的( ),求圆面积用公式表示( )。
长方形
周长一半
S=πr 2
半径
r
C
2
=
πr
我的收获
第 6 课时 圆 的 面 积(2)
第 二 单元 圆
1. 公园草地上的自动旋转喷水器的射程是8m。它能喷洒的面积是多少平方米?
S=8×8×3.14=200.96(平方米)
答:它能喷洒的面积是200.96平方米。
2. 一个圆形水缸口的外直径为1m。现在为这个水缸做一个盖子,这个盖子的面积至少是多少平方米?
S=(1÷2) ×3.14=0.785(平方米)
答:这个盖子的面积至少是0.785平方米。
半径(cm) 直径(cm) 周长(cm) 面积(cm2)
10
4
56.52
3.填空
5
31.4
78.5
9
8
25.12
50.24
18
254.34
4. 用下面这张长方形纸剪出一个最大的圆。
圆的直径是多少?
圆的面积是多少?
20cm
14cm
直径为14cm 面积:7×7×3.14=153.86(平方厘米)
张家村修了一个周长是251.2m的圆形蓄水池。它的占地面积是多少平方米?
它的半径:
251.2÷3.14÷2=40(米)
它的面积:
40×40×3.14
=5024(平方米)
答:它的占地面积是5024平方米。
8. 求下图中阴影部分的面积。(图中单位:cm)
6×6×3.14-2×2×3.14=100.46(cm )
10×10-5×5×3.14=21.5(cm )
把一个圆分成若干等份后,拼成近似的梯形或三角形,可以推算出圆面积计算公式吗?
3×3=9(c㎡)
5×3=15(c㎡)
6×3÷2=9(c㎡)
正方形面积=边长×边长
长方形面积=长×宽
三角形面积=底×高÷2
3cm
3cm
3cm
5cm
3cm
6cm
计算下面各图形的面积
3×4
=12(c㎡)
(6+4) ×3÷2
=15(c㎡)
3.14 ×32
=28.26(c㎡)
平行四边形的面积=底×高
圆的面积= 圆周率×半径的平方
梯形的面积=(上底+下底)×高÷2
3cm
3cm
3cm
4cm
4cm
6cm
计算下面各图形的面积
学校阅览室的窗户上面是半圆,下面是正方形。(如下图)窗户的面积约是多少平方米?
学校阅览室的窗户上面是半圆,下面是正方形。(如下图)窗户的面积约是多少平方米?
学校阅览室的窗户上面是半圆,下面是正方形。(如下图)窗户的面积约是多少平方米?
课堂活动
从正方形里截去一个最大的圆。
阴影部分的面积=正方形面积-圆的面积
3个图中的的阴影部分面积相等
1.议一议
涂色部分面积
=半圆形面积-小圆面积
2m
2m
6m
涂色部分面积
=长方形面积+圆面积
10cm
6cm
涂色部分面积
=外圆面积-内圆面积
涂色部分面积
=4个扇形面积之和
=一个圆面积
4.旋转餐厅的直径为36m,旋转部分宽7m。旋转部分的面积是多少平方米?
(36÷2) ×3.14-(36÷2-7) ×3.14=637.42(平方米)
3cm
3cm
课后拓展
求阴影部分的面积?
阴影部分的面积=(四分之一圆-三角形面积)×2
S=(3×3×3.14÷4-
3×3÷2)×2
=5.13(cm )
第 7 课时 组合图形的面积
第 二 单元 圆
一张可折叠的圆桌,半径是0.6m,折叠后成了正方形。折叠部分的面积约是多少平方米?(得数保留两位小数)
折叠部分面积=圆的面积-正方形面积
求圆形花坛周围小路的面积:
课堂活动
课堂活动
o
8m
10m
花坛周围小路的面积 = 外圆面积 - 内半圆面积
课堂活动
花坛外圆的面积:3.14×(8+2)2 =314(㎡)
花坛内圆的面积:3.14 ×82 =200.96 (㎡)
花坛小路的面积:314-200.96=113.04(㎡)
答:花坛周围的小路的面积是113.04 ㎡。
求图中阴影部分的面积。
4×4×3.14=50.24(cm )
一座雕塑的基座是圆形,半径为1.5m,在它的周围植上5m宽的环形草坪(如右图)。
(1)草坪的面积是多少平方米?
(2)如果植1m2草坪的成本为20元,那么植这块草坪的成本至少是多少元?
1.5m
5m
(1)(1.5+5) ÷3.14-1.5×1.5×3.14=125.6(m )
(2)125.6×20=2512(元)
用15.7m长的竹篱笆靠墙围一个半圆型鸡舍(如右图)。这个鸡舍的面积是多少平方米?
注意:15.7=πr≠2πr
第8课时 综合训练
第 二 单元 圆
画一画,算一算
1.画一个边长3cm的圆,用字母标出圆心、半径、直径,再画一条对称轴,计算出它的周长和面积。
2.用圆规设计一副美丽的图案。
两只小蚂蚁从a点出发到b点去取食物,它们选选择了两条不同的路线,谁选择的路线比较短?
求阴影部分的面积
阴影部分的面积=(四分之一圆-三角形面积)×2
S=(8×8×3.14÷4-
8×8÷2)×2
=36.48(cm )
求阴影部分的面积
阴影部分的面积=(四分之一圆-三角形面积)×8
S=(4×4×3.14÷4-
4×4÷2)×8
=36.48(cm )
求阴影部分的面积
两个半圆的面积相等,将其平移过来后,阴影部分的面积就是整个长方形面积的一半。 S=2×1÷2=1(m )
求阴影部分的面积
S=10×10×3.14÷4-
5×5×3.14÷2
=78.5-39.25
=39.25(cm )
下图中,阴影部分的面积是40cm2,求环形面积。
解决问题
R
r
阴影部分的面积=R -r
圆环的面积=R π-r π
=40×3.14
=125.6(cm )
游乐园的圆形高空转椅的直径是10m,如果每隔3.14m装一个吊篮,能装多少个吊篮?
解决问题
10×3.14÷3.14+1=11(个)
圆的认识
圆心
半径
直径
圆的周长
圆的面积
圆
圆周长、面积的拓展
圆形图案的设计制作
1.圆是一个什么样的图形?
圆是由一条曲线围成的封闭图形。属于平面图形中的一种。
圆的认识
圆的认识
2. 什么叫圆心?怎样确定一个圆的圆心?
o
圆心确定圆的位置。
圆的认识
3.什么是圆的半径、直径,在同圆或等圆中,它们有什么关系?
o
r
d
d=2r
半径(或直径)决定圆的大小。
r=d÷2
圆的周长
C=πd
C=2πr
C÷d=π
d=C÷π
圆周率表示什么?是一个什么样的小数?不同圆的圆周率一样吗?
圆的面积
4.什么叫圆的面积?怎么推导出圆面积计算的公式?
圆所占平面的大小叫做圆的面积。
圆的面积
将圆分成若干等分。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
1
2
3
4
5
6
7
8
16
15
14
13
12
11
10
9
将圆分成若干等分。
圆的面积
分的份数越多,拼成的图形越接近长方形。
r
C
2
圆的面积
r
C
2
=
πr
πr × r
S = πr 2
圆的面积 =
知道直径或者周长,怎么求面积?
圆的面积
与圆有关的结算公式
知道半径 (r) 知道直径 (d) 知道周长
(C)
求半径(r)
求直径(d)
求周长(C)
求面积(S)
r=d÷2
r=C÷π÷2
d=2r
d=C÷π
C=2πr
C=πd
S=πr2
S=π(d÷2)2
S=π(C÷π÷2)2
(1)两个半圆一定能拼成一个圆。 ( )
(2)半径是2厘米的圆,周长和面积相等( )
(3)大圆的圆周率比小圆的圆周率大。 ( )
×
×
×
(4)半圆形纸片的周长就是圆周长的一半。( )
(5)把半径3厘米的圆等分成十六份,拼成一个近似长方形,长方形的周长比圆的周长长。 ( )
×
√
判断
(6)在同一个圆内可以画100条直径。
(7)所有的圆的直径都相等。
(8)等圆的半径都相等。
(9)两端都在圆上的线段叫做直径。
(10)圆心到圆上任意一点的距离都相等。
(11)半径是2cm的圆比直径是3cm的圆大。
( )
( )
( )
( )
√
×
×
×
( )
( )
√
√
判断
(1)圆中心的一点叫做( ),一般用字母( )表示。
(2) 连接圆心和圆上任意一点的线段叫做( ),一般用字母r 表示。
(3) 通过圆心并且两端都在圆上的线段叫做( ),一般用字母d 表示。
(4)一个圆内有( )条直径,( )条半径。并且( )条直径的长等于2 条半径的长。
圆心
O
半径
直径
无数
无数
1
填空
(5)圆是( )图形,有( )条对称轴。
(6) 把圆规的两脚分开,定好两脚间的距离作( )。
(7)圆是平面上的一种( )图形。圆的两条直径的交点是圆的( )。
(8)把一个圆形纸片沿半径平均分成若干等份,拼成一个近似的长方形。则面积( ),周长( )。
轴对称
半径
无数
填空
不变
增加
曲线
圆心
(9)周长相等的圆、正方形和长方形,( )的面积最大。
(10)圆中最长的线段是圆的( )。
(11)把一个直径是10cm的圆剪成两个半圆,则两个半圆周长的和是( )cm。
(12)用圆规画一个周长12.56cm的圆,圆规两脚之间的距离是( )cm,所画圆的面积是( )平方厘米。
圆
直径
51.4
填空
2
12.56
(13)圆的半径扩大3倍,直径扩大( )倍,周长扩大( )倍;面积扩大( )倍。
(14)小铁环直径6dm,大铁环直径8dm。大铁环和小铁环半径的比是( );周长的比是( );面积的比是( )。如果它们滚过相同的路程,则转动的圈数的比是( )。
(15)在一张长60cm,宽40cm的长方形纸上剪一个最大的圆,则圆的面积是( )cm2。
3
3
9
3:4
3:4
9:16
4:3
1256
填空
(1)画圆时,圆规两脚间的距离是( )。
A.半径长度 B.直径长度
(2)从圆心到( )任意一点的线段叫半径。
A.圆心 B.圆外 C.圆上
(3)通过圆心并且两端都在圆上的( )叫直径。
A.直线 B.线段 C.射线
A
C
B
选择
