沪科版八年级下册数学 18.2 勾股定理的逆定理课件 (共14张PPT)
文档属性
| 名称 | 沪科版八年级下册数学 18.2 勾股定理的逆定理课件 (共14张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-19 00:00:00 | ||
图片预览






文档简介
(共14张PPT)
18.2勾股定理的逆定理
学习目标:
1.会用勾股定理的逆定理解决实际问题。
2.树立数形结合的思想。
3.探究勾股定理逆定理在实际问题中的应用,感受它的应用方法。
重点:勾股定理逆定理的应用。
难点:实际问题向数学问题的转化。
预学检测
1、你知道勾股定理逆定理的内容吗?
2、勾股定理逆定理的应用条件是什么?
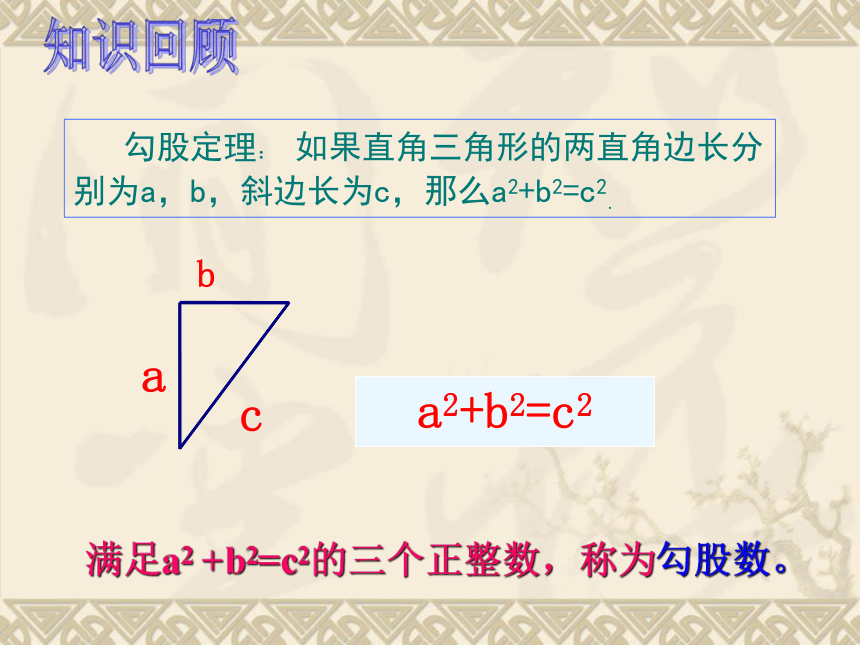
勾股定理:
如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
b
a2+b2=c2
a
c
满足a2
+b2=c2的三个正整数,称为勾股数。
古埃及人曾用下面的方法画直角:他们把一根长绳打上等距离的13个结,然后以3个结、4个结、5个结的长度为边长,用木桩钉成一个三角形,其中一个角便是直角。
他们真的能够得到直角三角形吗?
情境体验
动手画一画
下面的三组数分别是一个三角形的三边长a,b,c:
5,12,13;
6,8,10;
3,4,5。
猜想命题2
如果三角形的三边长a,b,c满足
请与你的同伴合作,看看可以找出多少组能够组成直角三角形的边长。
例题分析;
例1
题略。
例2
已知:在△ABC中,三条边长分别为a=n2-1,b=2n,c=n2+1(n﹥1).求证:
△ABC为直角三角形。
勾股数
勾股定理的逆定理的主要应用
勾股定理的逆定理主要用于判断三角形是否为直角三角形。
当堂训练:
一、P59页1、2、3、4.
二、习题18.2
1、5、6、7
知识应用
解
∵
a2c2-
b2c2
=
a4
–
b4
(1)
∴
c2(a2
–
b2)
=
(a2+
b2)
(a2-
b2)
(2)
∴
c2
=
a2
+
b2
(3)
∴
△ABC是直角三角形
问:
(1)
上述解题过程,从哪一步开始出现错误?请写出该步的代号___
(2)
错误原因是_________
(3)
本题正确的结论是________
3
a2-
b2可能是0
直角三角形或等腰三角形
三.已知a.b.c为△ABC的三边,满足
,试判断△ABC的形状.
判定一个三角形是否是直角三角形有几种方法
方法一:可以根据角的度数来判断
方法二:如果三角形的三边长a,b,c满足
那么这个三角形是直角三角形
归纳
总结提升
本节你学会了哪些内容?试着向同学们说一说。
勾股定理的逆定理你会用了吗?
本节中你最大的收获是什么?
布置作业
课堂作业
习题18.2
2、3;第4题选择做.
家庭作业
基训:18.2
(1),(2).
18.2勾股定理的逆定理
学习目标:
1.会用勾股定理的逆定理解决实际问题。
2.树立数形结合的思想。
3.探究勾股定理逆定理在实际问题中的应用,感受它的应用方法。
重点:勾股定理逆定理的应用。
难点:实际问题向数学问题的转化。
预学检测
1、你知道勾股定理逆定理的内容吗?
2、勾股定理逆定理的应用条件是什么?
勾股定理:
如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
b
a2+b2=c2
a
c
满足a2
+b2=c2的三个正整数,称为勾股数。
古埃及人曾用下面的方法画直角:他们把一根长绳打上等距离的13个结,然后以3个结、4个结、5个结的长度为边长,用木桩钉成一个三角形,其中一个角便是直角。
他们真的能够得到直角三角形吗?
情境体验
动手画一画
下面的三组数分别是一个三角形的三边长a,b,c:
5,12,13;
6,8,10;
3,4,5。
猜想命题2
如果三角形的三边长a,b,c满足
请与你的同伴合作,看看可以找出多少组能够组成直角三角形的边长。
例题分析;
例1
题略。
例2
已知:在△ABC中,三条边长分别为a=n2-1,b=2n,c=n2+1(n﹥1).求证:
△ABC为直角三角形。
勾股数
勾股定理的逆定理的主要应用
勾股定理的逆定理主要用于判断三角形是否为直角三角形。
当堂训练:
一、P59页1、2、3、4.
二、习题18.2
1、5、6、7
知识应用
解
∵
a2c2-
b2c2
=
a4
–
b4
(1)
∴
c2(a2
–
b2)
=
(a2+
b2)
(a2-
b2)
(2)
∴
c2
=
a2
+
b2
(3)
∴
△ABC是直角三角形
问:
(1)
上述解题过程,从哪一步开始出现错误?请写出该步的代号___
(2)
错误原因是_________
(3)
本题正确的结论是________
3
a2-
b2可能是0
直角三角形或等腰三角形
三.已知a.b.c为△ABC的三边,满足
,试判断△ABC的形状.
判定一个三角形是否是直角三角形有几种方法
方法一:可以根据角的度数来判断
方法二:如果三角形的三边长a,b,c满足
那么这个三角形是直角三角形
归纳
总结提升
本节你学会了哪些内容?试着向同学们说一说。
勾股定理的逆定理你会用了吗?
本节中你最大的收获是什么?
布置作业
课堂作业
习题18.2
2、3;第4题选择做.
家庭作业
基训:18.2
(1),(2).
