华东师大版七年级下册数学: 9.1 .3 三角形的三边关系 课件(共34张PPT)
文档属性
| 名称 | 华东师大版七年级下册数学: 9.1 .3 三角形的三边关系 课件(共34张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-18 00:00:00 | ||
图片预览










文档简介
(共34张PPT)
9.1.3
三角形的三边关系
像这样由不在同一直线上的三条线段首尾相接围成的平面图形叫三角形。
问题一:三角形的外角性质有哪些?
提问
问题二:在连接两点的所有线中,
最短的是哪一种?
1.三角形的一个外角等于与它不相邻的两个内角之和;
2.三角形的一个外角大于与它不相邻的一个内角;
线段最短
画一个三角形,使它的三边长分别为
①2cm、3cm、4cm.
②2cm、3cm、5cm.
③2cm、3cm、6cm.
课前预习:
我们发现,并不是所有的三条线段都能围成三角形。若能围成三角形,三条线段应该具有怎样的关系?
两条线段长度的和大于第三条线段。
两条线段长度的和等于第三条线段。
两条线段长度的和小于第三条线段。
大胆猜测:
两根小棒的长度和与第三根小棒存在什么关系时,就能围成三角形呢?
当两根小棒的长度和大于第三根小棒时,能围成三角形。
猜想2:
当两根小棒的长度和等于第三根小棒时,能围成三角形。
猜想3:
猜想1:
当两根小棒的长度和小于第三根小棒时,能围成三角形。
当两根小棒的长度和等于第三根小棒时,
不能围成三角形。
当两根小棒的长度和小于第三根小棒时,
不能围成三角形。
当两根小棒的长度和大于第三根小棒时,
当两根小棒的长度和大于第三根小棒时,
能围成三角形。
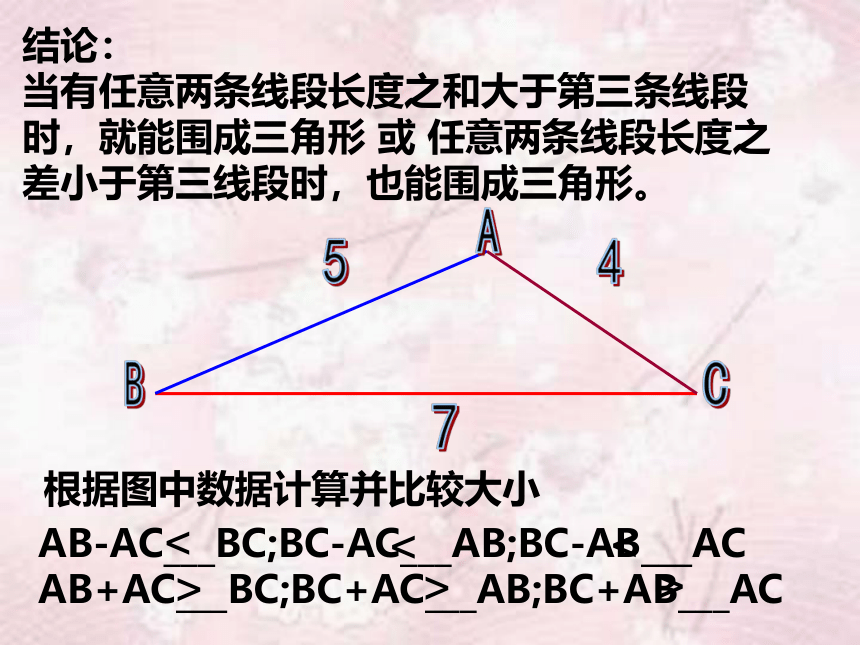
结论:
当有任意两条线段长度之和大于第三条线段时,就能围成三角形
或
任意两条线段长度之差小于第三线段时,也能围成三角形。
根据图中数据计算并比较大小
AB-AC___BC;BC-AC___AB;BC-AB___AC
AB+AC___BC;BC+AC___AB;BC+AB___AC
<
<
<
>
>
>
结论:
三角形任意两边之和大于第三边,任意两边之差小于第三边。
例题:
判断:3厘米,4厘米,6厘米三条线段能否围成三角形?
因为:3+4>6,4+6>3,3+6>4
所以:能围成三角形。
我们能不能有更好的办法来判断已知三条线段能否围成三角形?
用两个较小边长度之和,和最大边做比较,如果大于则能围成,反之不能。
或用两个较大边长度之差,和最小边去比较,如果小于则能围成,反之不能。
习题:
判别下列线段能否围成三角形。
1.2cm,3cm,4cm;
2.3cm,2cm,5cm;
3.5cm,1cm,3cm;
4.3cm,4cm,8cm;
5.4cm,4cm,4cm;
6.5cm,5cm,6cm;
7.3cm,7cm,9cm;
8.5cm,4cm,12cm;
A
B
C
a
c
b
三角形三边的关系
三角形两边
的和大于第三边
三角形两边
的差小于第三边
a-bc-bc-ab+c>a
a+c>b
a+b>c
由此得出:
两边的差
<
第三边
<
两边的和.
现有两根木条a和b,a长10cm,b长
3cm,如果再找一根木条钉成一个三角形木框,那么
对第三根木条c的长度有什么要求?
分析:
如果设木条c的长为xcm,那么仅有小于两边之和还不够,仅有大于两边之差也不行,必须同时满足x<10+3和
x>10-3。
即{
解得,7
<
x
<
13
答:第三根木条的长度应在7㎝和13㎝之间。
例1、
小颖要制作一个三角形木架,现有两根长度为8cm和5cm的木棒,如果要求第三根木棒的长度是偶数,小颖有几种选法?第三根的长度可以是多少?
小颖有5种选法。
第三根木棒的长度可以是:4cm,6cm,8cm,10cm,12cm
做一做
在我校有说大话的同学,说自己步子大,一步能走3米多,你相信吗?说说你的理由!
考考你!
2、已知两条边长分别为2cm、5cm,
你可以画出几个符合条件的等腰三角形?
讨论解疑:
1、已知两条边长分别为3cm、5cm,你可以
画出几个符合条件的等腰三角形?并求符合
条件的等腰三角形的周长.
公路两旁的路灯上面都有一个三角形的架子,而办公楼的推拉门是由许多个平行四边形组成的。为什么不能让路灯上的三角形安装到伸缩门里呢?为什么不能让伸缩门里的平行四边形安装到路灯上面呢?
疑问:
1、将三根木条用钉子钉成一个三角形木架,然后扭动它,它的形状会改变吗?
没有改变
2、将四根木条用钉子钉成一个四边形木架,然后扭动它,它的形状会改变吗?
易变形
3、在四边形木架上再钉一根木条,将它的一对顶点连接起来,然后扭动它,它的形状会改变吗?
不易变形
三角形具有稳定性:
只要三角形三条边的长度固定,这个三角形的形状和大小也就完全确定,三角形的这种性质叫做三角形的稳定性。
生活中的三角形
等腰△ABC中,AB=AC。BD为AC边上中线,已知AB=8,BC=3,则△ABD的周长与△BCD周长之差是多少?
A
B
C
D
如图所示,已知P是△ABC内一点,求证,PA+PB+PC>1/2(AB+BC+AC)
A
B
C
P
证明:
在△ABP中,PA+PB>AB①
在△ACP中,
PA+PC>AC②
在△BCP中,
PB+PC>BC③
①+②+③得:
2(PA+PB+PC)>AB+BC+AC
即:PA+PB+PC>
1/2(AB+BC+AC)
1.怎样应用三边关系判断三条线段能否组成三角形 应该怎样选择边进行比较?
2.三角形是否具有稳定性?四边形呢?
总结
三角形的任何两边之和大于第三边。
应该以较小的两边的和与较长边进行比较。
三角形具有稳定性,四边形不具有稳定性。
作业:
教科书82页,练习:1.2.3.习题8.2第1题。
9.1.3
三角形的三边关系
像这样由不在同一直线上的三条线段首尾相接围成的平面图形叫三角形。
问题一:三角形的外角性质有哪些?
提问
问题二:在连接两点的所有线中,
最短的是哪一种?
1.三角形的一个外角等于与它不相邻的两个内角之和;
2.三角形的一个外角大于与它不相邻的一个内角;
线段最短
画一个三角形,使它的三边长分别为
①2cm、3cm、4cm.
②2cm、3cm、5cm.
③2cm、3cm、6cm.
课前预习:
我们发现,并不是所有的三条线段都能围成三角形。若能围成三角形,三条线段应该具有怎样的关系?
两条线段长度的和大于第三条线段。
两条线段长度的和等于第三条线段。
两条线段长度的和小于第三条线段。
大胆猜测:
两根小棒的长度和与第三根小棒存在什么关系时,就能围成三角形呢?
当两根小棒的长度和大于第三根小棒时,能围成三角形。
猜想2:
当两根小棒的长度和等于第三根小棒时,能围成三角形。
猜想3:
猜想1:
当两根小棒的长度和小于第三根小棒时,能围成三角形。
当两根小棒的长度和等于第三根小棒时,
不能围成三角形。
当两根小棒的长度和小于第三根小棒时,
不能围成三角形。
当两根小棒的长度和大于第三根小棒时,
当两根小棒的长度和大于第三根小棒时,
能围成三角形。
结论:
当有任意两条线段长度之和大于第三条线段时,就能围成三角形
或
任意两条线段长度之差小于第三线段时,也能围成三角形。
根据图中数据计算并比较大小
AB-AC___BC;BC-AC___AB;BC-AB___AC
AB+AC___BC;BC+AC___AB;BC+AB___AC
<
<
<
>
>
>
结论:
三角形任意两边之和大于第三边,任意两边之差小于第三边。
例题:
判断:3厘米,4厘米,6厘米三条线段能否围成三角形?
因为:3+4>6,4+6>3,3+6>4
所以:能围成三角形。
我们能不能有更好的办法来判断已知三条线段能否围成三角形?
用两个较小边长度之和,和最大边做比较,如果大于则能围成,反之不能。
或用两个较大边长度之差,和最小边去比较,如果小于则能围成,反之不能。
习题:
判别下列线段能否围成三角形。
1.2cm,3cm,4cm;
2.3cm,2cm,5cm;
3.5cm,1cm,3cm;
4.3cm,4cm,8cm;
5.4cm,4cm,4cm;
6.5cm,5cm,6cm;
7.3cm,7cm,9cm;
8.5cm,4cm,12cm;
A
B
C
a
c
b
三角形三边的关系
三角形两边
的和大于第三边
三角形两边
的差小于第三边
a-b
a+c>b
a+b>c
由此得出:
两边的差
<
第三边
<
两边的和.
现有两根木条a和b,a长10cm,b长
3cm,如果再找一根木条钉成一个三角形木框,那么
对第三根木条c的长度有什么要求?
分析:
如果设木条c的长为xcm,那么仅有小于两边之和还不够,仅有大于两边之差也不行,必须同时满足x<10+3和
x>10-3。
即{
解得,7
<
x
<
13
答:第三根木条的长度应在7㎝和13㎝之间。
例1、
小颖要制作一个三角形木架,现有两根长度为8cm和5cm的木棒,如果要求第三根木棒的长度是偶数,小颖有几种选法?第三根的长度可以是多少?
小颖有5种选法。
第三根木棒的长度可以是:4cm,6cm,8cm,10cm,12cm
做一做
在我校有说大话的同学,说自己步子大,一步能走3米多,你相信吗?说说你的理由!
考考你!
2、已知两条边长分别为2cm、5cm,
你可以画出几个符合条件的等腰三角形?
讨论解疑:
1、已知两条边长分别为3cm、5cm,你可以
画出几个符合条件的等腰三角形?并求符合
条件的等腰三角形的周长.
公路两旁的路灯上面都有一个三角形的架子,而办公楼的推拉门是由许多个平行四边形组成的。为什么不能让路灯上的三角形安装到伸缩门里呢?为什么不能让伸缩门里的平行四边形安装到路灯上面呢?
疑问:
1、将三根木条用钉子钉成一个三角形木架,然后扭动它,它的形状会改变吗?
没有改变
2、将四根木条用钉子钉成一个四边形木架,然后扭动它,它的形状会改变吗?
易变形
3、在四边形木架上再钉一根木条,将它的一对顶点连接起来,然后扭动它,它的形状会改变吗?
不易变形
三角形具有稳定性:
只要三角形三条边的长度固定,这个三角形的形状和大小也就完全确定,三角形的这种性质叫做三角形的稳定性。
生活中的三角形
等腰△ABC中,AB=AC。BD为AC边上中线,已知AB=8,BC=3,则△ABD的周长与△BCD周长之差是多少?
A
B
C
D
如图所示,已知P是△ABC内一点,求证,PA+PB+PC>1/2(AB+BC+AC)
A
B
C
P
证明:
在△ABP中,PA+PB>AB①
在△ACP中,
PA+PC>AC②
在△BCP中,
PB+PC>BC③
①+②+③得:
2(PA+PB+PC)>AB+BC+AC
即:PA+PB+PC>
1/2(AB+BC+AC)
1.怎样应用三边关系判断三条线段能否组成三角形 应该怎样选择边进行比较?
2.三角形是否具有稳定性?四边形呢?
总结
三角形的任何两边之和大于第三边。
应该以较小的两边的和与较长边进行比较。
三角形具有稳定性,四边形不具有稳定性。
作业:
教科书82页,练习:1.2.3.习题8.2第1题。
