人教版九年级数学下册 27.2.1相似三角形的判定——三边成比例或两边成比例且夹角相等的两个三角形相似课件(共40张PPT)
文档属性
| 名称 | 人教版九年级数学下册 27.2.1相似三角形的判定——三边成比例或两边成比例且夹角相等的两个三角形相似课件(共40张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-19 11:24:51 | ||
图片预览








文档简介
(共40张PPT)
27.2.1
相似三角形的判定
第2课时
三边成比例或两边成比例
且尖角相等的两个三角形相似
27
相
似
学习目标
教学分析
1.经历探究两个三角形相似的过程,获得探究数学结论的体验,进一步发展探究、分析、归纳与归纳能力.
2.掌握两个三角形相似的判定条件:相似三角形的定义和相似三角形的预备定理(平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
3.会运用“三角形相似的预备定理”解决简单的问题.
导入新课
学习三角形全等时,我们知道,除了可以通过证明对应角相等.对应边相等来判定两个三角形全等外,还有判定的简便方法(SSS、SAS、ASA、AAS).类似地,判定两个三角形相似时,是不是对所有的对应角和对应边都要一一验证呢?
不需要
导入新课
类似于判定三角形全等的SSS方法,我们能不能通过三边来判断两个
三角形相似呢?
能
合作探究
探究点一
三边之比相等与
三角形相似
合作探究
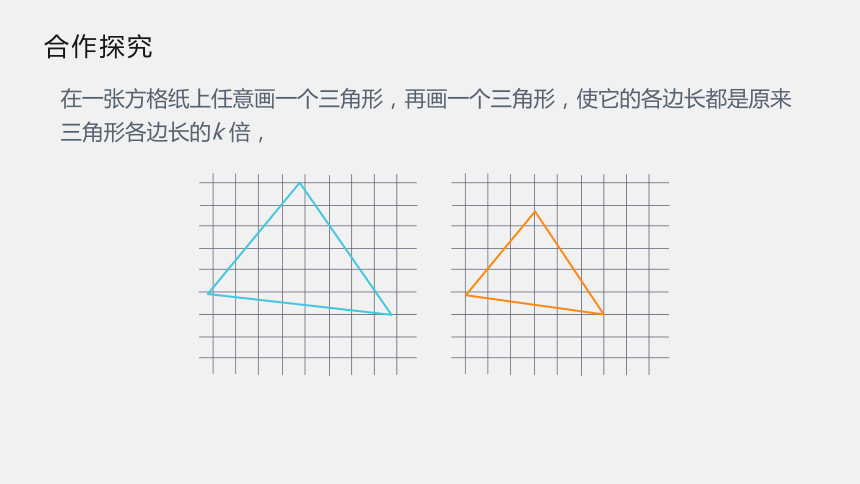
在一张方格纸上任意画一个三角形,再画一个三角形,使它的各边长都是原来三角形各边长的k
倍,
合作探究
度量这两个三角形的对应角,它们相等吗?这两个三角形相似吗?
这两个三角形是相似的.
在△ABC
和△A'B'C'
中,
求证:
△ABC∽△A'B'C'
合作探究
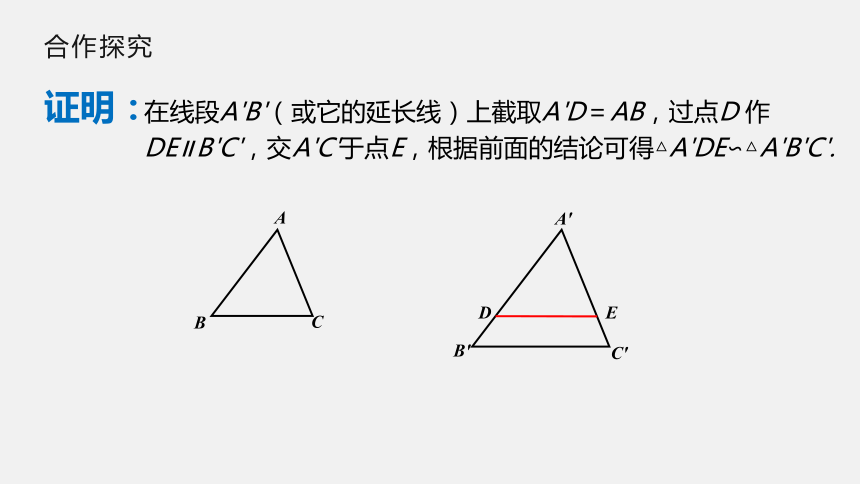
证明:
在线段A'B'(或它的延长线)上截取A'D=AB,过点D
作DE∥B'C',交A'C'于点E,根据前面的结论可得△A'DE∽△A'B'C'.
A'
B'
C'
D
E
A
B
C
合作探究
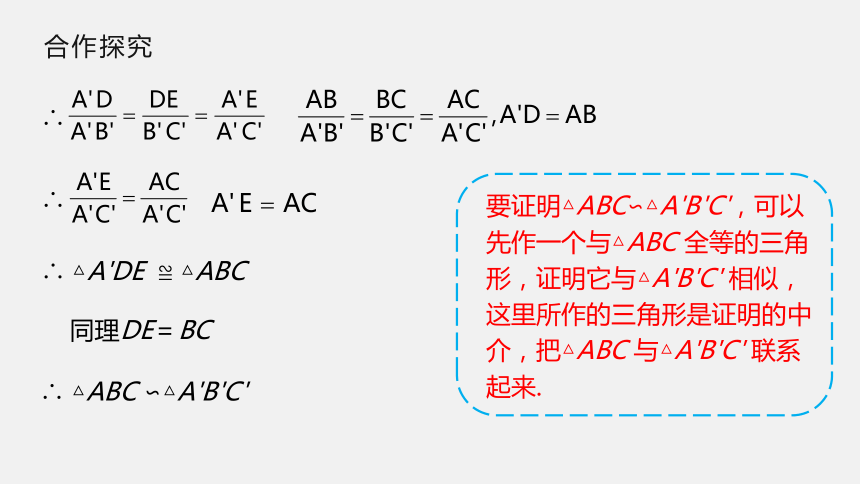
同理DE=BC
∴
△A'DE
≌
△ABC
∴
△ABC
∽△A'B'C'
∴
∴
要证明△ABC∽△A'B'C',可以先作一个与△ABC
全等的三角形,证明它与△A'B'C'
相似,这里所作的三角形是证明的中介,把△ABC
与△A'B'C'
联系起来.
合作探究
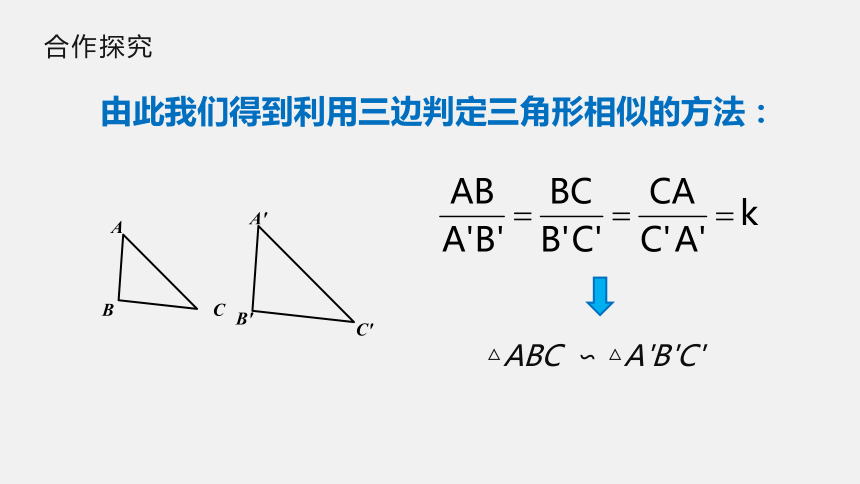
由此我们得到利用三边判定三角形相似的方法:
A'
B'
C'
A
B
C
△ABC
∽
△A'B'C'
合作探究
如果两个三角形的三组对应边的比
相等,那么这两个三角形相似.
合作探究
小组讨论
1
在用三边的比判定两个三角形相似时,如何寻找对应边?
合作探究
反思小结
利用三边的比判定两个三角形相似时,
应先将两个三角形的三边按大小顺序排列,
然后分别计算它们对应边的比,
最后由比值是否相等来确定两个三角形是否相似.
合作探究
1.
如图,若
=
=
则△______∽△______.
ADE
ABC
针对训练
1
合作探究
2.
若一个三角形的三边长分别为6cm,9cm,7.5cm,
另一个三角形的三边长分别为12cm,18cm,
________时,这两个三角形相似.
15cm
合作探究
3.
(1)根据下面条件,判断△ABC与△A′B′C′是否相似,并说明理由.
AB=4cm,BC=6cm,AC=8cm,
A′B′=12cm,B′C′=18cm,A′C′=
21cm.
(2)若(1)中两三角形不相似,那么要使它俩相似,
不改变AC的长,A′C′的长应当改为多少?
答:△ABC与△A′B′C′的三组对应边的比不等,它们不相似;
答:当A′C′=24cm时,两个三角形相似.
合作探究
探究点二
两边之比及夹角对应
与三角形相似
合作探究
2.改变∠A
或K
值的大小,再试一试,是否有同样的结论?
利用刻度尺和量角器画△ABC
和△A'B'C',使∠A=∠A',
和
都等于给定的值k,量出它们的第三组对应边BC
和B'C'
的长,
1.它们的比等于k
吗?另外两组对应角∠B
与∠B
',∠C
与∠C
'是否相等?
答:等于k
∠B
=∠B
'
∠C
=∠C
'
答:改变k
的值具有相同的结论.
合作探究
实际上,我们有利用两边和夹角判定两个三角形相似的方法:
A'
B'
C'
A
B
C
∠A=∠A'
△ABC
∽
△A'B'C'
合作探究
如图,
△A'B'C'
和
△ABC
中,
∠A
'
=∠A,
A'B':AB=A'C':AC
已知:
求证:
△A'B'C'
∽
△ABC
A'
B'
C'
A
B
C
D
E
合作探究
证明:
在△ABC
的边AB、AC(或它们的延长线)上分别截取AD=A'B',AE=A'C',
连结DE,因∠A
'
=∠A,
这样△A'B'C'
≌
△ADE
.
∴
DE//BC
∴
△ADE
∽
△ABC
∴
△A'B'C'
∽
△ABC
合作探究
如果两个三角形的两组对应边的比相等,
并且相应的夹角相等,
那么这两个三角形相似.
(
类似于证明通过三边判定三角形相似的方法,
请你自己证明这个结论.)
合作探究
思考:
对于△ABC
和△A'B'C',
如果
,∠B=∠B
',
这两个三角形一定相似吗?试着画画看.
不一定相似
合作探究
小组讨论
2
由两边和夹角判定两个三角形相似时,对于“夹角”条件,如何理解?
可结合具体图形说明.
合作探究
反思小结
由两边和夹角判定三角形相似时,
要注意这个角是对应边成比例的两边的夹角.
合作探究
例1
根据下列条件,判断△ABC
与△A'B'C
'是否相似,并说明理由:
(1)∠A=120°,AB=7cm,AC=14cm,
∠A'=120°,A'B'=3cm,A'C'=6cm;
解:
∵
AB=7cm,
AC=14cm,
A'B'=3cm,A'C'=6cm.
又
∠A=∠A'
∴
△ABC∽△A'B'C'
两三角形的相似比是多少?
合作探究
(2)
AB=4cm,BC=6cm,
AC=8cm.
A'B'=12cm,B'C'=18cm,
A'C'=21cm.
∵
解:
∴
要使两三角形相似,不改变AC
的长,A'C
'的长应当改为多少?
合作探究
若∠DAE=∠BAC,
则△ADE∽△ABC.
=
针对训练
2
合作探究
根据下面条件,判断△ABC与△A′B′C′
是否相似,并说明理由.
∠A=120°,AB=7cm,AC=14cm;
∠A=120°,A′B′=3cm,A′C′=6cm.
解:
∵
,
,
∴
.
又∠A=∠A′,∴△ABC∽△A′B′C′.
课堂小结
概念、
性质
1.如果两个三角形的三组对应边的比相等,那么这两个三角形
_________.
2.如果两个三角形的两组对应边的比________,并且相应的夹角_________
那么这两个三角形相似.
方法、规律
1.解答方格中的相似三角形问题时,通常采用三边对应成比例的两个三角形相似,以及两边对应成比例且它们的夹角相等的两个三角形相似进行分析.
相似
相等
相等
课堂小结
易错点
如左图,由∠DAC=∠CAB,
并不能证明△ACD∽△ABC.这和全等三角形不存在“SSA”这种判定方法一样,可以类比记忆.
”相似“与”∽“:在用符号”∽“表示两个三角形相似时,表明对应顺序已确定,只存在一种相似情况.用”相似“表示两个三角形相似时,表明对应顺序没有确定,需要分类讨论.
巩固扩展
1.下列条件中,能判定△ABC∽△A'B'C'的是(
)
B
巩固扩展
2.
在△ABC和△A′B′C′中,
若∠B=∠B′,AB=12,BC=8,A′B′=6,
则当B′C′=______时,
△ABC∽△A′B′C′.
4
巩固扩展
3.
(1)如图1,请你增加一个条件:
,使△ABC∽△ACD.
AB
(
)
=
(
)
(
)
(2)如图2,请你增加一个条件:
,使△ABC∽△AED.
AB
(
)
=
(
)
(
)
AC
AC
AD
AE
AC
AD
巩固扩展
(3)如图3,请你增加一个条件:
使△ABC∽△ADE.
AB
(
)
=
(
)
(
)
(4)如图4,请你增加一个条件:
使△ABC∽△ADE.
AB
(
)
=
(
)
(
)
AD
AE
AC
AD
AE
AC
巩固扩展
(5)如图5,AC与BD不平行,请你增加一个条件
OA
(
)
=
(
)
(
)
使△AOC∽△DOB.
OC
OD
OB
巩固扩展
4.
如图,在△ABC中,
D,E分别是AB,AC上的点,
AB=7.8,BD=4.8,AC=6,AE=3.9,
试判断△ADE与△ABC是否相似,
某同学的解答如下:
巩固扩展
解:
∵
AB=AD+BD,而AB=7.8,BD=4.8,
∴
AD=7.8-4.8=3.
∵
∴
这两个三角形不相似.
你同意他的判断吗?请说明理由.
巩固扩展
解:
他的判断是错误的.
∵
AB=AD+BD,而AB=7.8,BD=4.8,
∴
AD=7.8-4.8=3.
∵
∴
又
∵
∠A=∠A,
∴
△ADE∽△ACB
.
巩固扩展
5.
如图,在4×4的方格图中,△ABC和△DEF都在边长为1的小正方形的顶点上,
求证:△ABC∽△DEF.
27.2.1
相似三角形的判定
第2课时
三边成比例或两边成比例
且尖角相等的两个三角形相似
27
相
似
学习目标
教学分析
1.经历探究两个三角形相似的过程,获得探究数学结论的体验,进一步发展探究、分析、归纳与归纳能力.
2.掌握两个三角形相似的判定条件:相似三角形的定义和相似三角形的预备定理(平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
3.会运用“三角形相似的预备定理”解决简单的问题.
导入新课
学习三角形全等时,我们知道,除了可以通过证明对应角相等.对应边相等来判定两个三角形全等外,还有判定的简便方法(SSS、SAS、ASA、AAS).类似地,判定两个三角形相似时,是不是对所有的对应角和对应边都要一一验证呢?
不需要
导入新课
类似于判定三角形全等的SSS方法,我们能不能通过三边来判断两个
三角形相似呢?
能
合作探究
探究点一
三边之比相等与
三角形相似
合作探究
在一张方格纸上任意画一个三角形,再画一个三角形,使它的各边长都是原来三角形各边长的k
倍,
合作探究
度量这两个三角形的对应角,它们相等吗?这两个三角形相似吗?
这两个三角形是相似的.
在△ABC
和△A'B'C'
中,
求证:
△ABC∽△A'B'C'
合作探究
证明:
在线段A'B'(或它的延长线)上截取A'D=AB,过点D
作DE∥B'C',交A'C'于点E,根据前面的结论可得△A'DE∽△A'B'C'.
A'
B'
C'
D
E
A
B
C
合作探究
同理DE=BC
∴
△A'DE
≌
△ABC
∴
△ABC
∽△A'B'C'
∴
∴
要证明△ABC∽△A'B'C',可以先作一个与△ABC
全等的三角形,证明它与△A'B'C'
相似,这里所作的三角形是证明的中介,把△ABC
与△A'B'C'
联系起来.
合作探究
由此我们得到利用三边判定三角形相似的方法:
A'
B'
C'
A
B
C
△ABC
∽
△A'B'C'
合作探究
如果两个三角形的三组对应边的比
相等,那么这两个三角形相似.
合作探究
小组讨论
1
在用三边的比判定两个三角形相似时,如何寻找对应边?
合作探究
反思小结
利用三边的比判定两个三角形相似时,
应先将两个三角形的三边按大小顺序排列,
然后分别计算它们对应边的比,
最后由比值是否相等来确定两个三角形是否相似.
合作探究
1.
如图,若
=
=
则△______∽△______.
ADE
ABC
针对训练
1
合作探究
2.
若一个三角形的三边长分别为6cm,9cm,7.5cm,
另一个三角形的三边长分别为12cm,18cm,
________时,这两个三角形相似.
15cm
合作探究
3.
(1)根据下面条件,判断△ABC与△A′B′C′是否相似,并说明理由.
AB=4cm,BC=6cm,AC=8cm,
A′B′=12cm,B′C′=18cm,A′C′=
21cm.
(2)若(1)中两三角形不相似,那么要使它俩相似,
不改变AC的长,A′C′的长应当改为多少?
答:△ABC与△A′B′C′的三组对应边的比不等,它们不相似;
答:当A′C′=24cm时,两个三角形相似.
合作探究
探究点二
两边之比及夹角对应
与三角形相似
合作探究
2.改变∠A
或K
值的大小,再试一试,是否有同样的结论?
利用刻度尺和量角器画△ABC
和△A'B'C',使∠A=∠A',
和
都等于给定的值k,量出它们的第三组对应边BC
和B'C'
的长,
1.它们的比等于k
吗?另外两组对应角∠B
与∠B
',∠C
与∠C
'是否相等?
答:等于k
∠B
=∠B
'
∠C
=∠C
'
答:改变k
的值具有相同的结论.
合作探究
实际上,我们有利用两边和夹角判定两个三角形相似的方法:
A'
B'
C'
A
B
C
∠A=∠A'
△ABC
∽
△A'B'C'
合作探究
如图,
△A'B'C'
和
△ABC
中,
∠A
'
=∠A,
A'B':AB=A'C':AC
已知:
求证:
△A'B'C'
∽
△ABC
A'
B'
C'
A
B
C
D
E
合作探究
证明:
在△ABC
的边AB、AC(或它们的延长线)上分别截取AD=A'B',AE=A'C',
连结DE,因∠A
'
=∠A,
这样△A'B'C'
≌
△ADE
.
∴
DE//BC
∴
△ADE
∽
△ABC
∴
△A'B'C'
∽
△ABC
合作探究
如果两个三角形的两组对应边的比相等,
并且相应的夹角相等,
那么这两个三角形相似.
(
类似于证明通过三边判定三角形相似的方法,
请你自己证明这个结论.)
合作探究
思考:
对于△ABC
和△A'B'C',
如果
,∠B=∠B
',
这两个三角形一定相似吗?试着画画看.
不一定相似
合作探究
小组讨论
2
由两边和夹角判定两个三角形相似时,对于“夹角”条件,如何理解?
可结合具体图形说明.
合作探究
反思小结
由两边和夹角判定三角形相似时,
要注意这个角是对应边成比例的两边的夹角.
合作探究
例1
根据下列条件,判断△ABC
与△A'B'C
'是否相似,并说明理由:
(1)∠A=120°,AB=7cm,AC=14cm,
∠A'=120°,A'B'=3cm,A'C'=6cm;
解:
∵
AB=7cm,
AC=14cm,
A'B'=3cm,A'C'=6cm.
又
∠A=∠A'
∴
△ABC∽△A'B'C'
两三角形的相似比是多少?
合作探究
(2)
AB=4cm,BC=6cm,
AC=8cm.
A'B'=12cm,B'C'=18cm,
A'C'=21cm.
∵
解:
∴
要使两三角形相似,不改变AC
的长,A'C
'的长应当改为多少?
合作探究
若∠DAE=∠BAC,
则△ADE∽△ABC.
=
针对训练
2
合作探究
根据下面条件,判断△ABC与△A′B′C′
是否相似,并说明理由.
∠A=120°,AB=7cm,AC=14cm;
∠A=120°,A′B′=3cm,A′C′=6cm.
解:
∵
,
,
∴
.
又∠A=∠A′,∴△ABC∽△A′B′C′.
课堂小结
概念、
性质
1.如果两个三角形的三组对应边的比相等,那么这两个三角形
_________.
2.如果两个三角形的两组对应边的比________,并且相应的夹角_________
那么这两个三角形相似.
方法、规律
1.解答方格中的相似三角形问题时,通常采用三边对应成比例的两个三角形相似,以及两边对应成比例且它们的夹角相等的两个三角形相似进行分析.
相似
相等
相等
课堂小结
易错点
如左图,由∠DAC=∠CAB,
并不能证明△ACD∽△ABC.这和全等三角形不存在“SSA”这种判定方法一样,可以类比记忆.
”相似“与”∽“:在用符号”∽“表示两个三角形相似时,表明对应顺序已确定,只存在一种相似情况.用”相似“表示两个三角形相似时,表明对应顺序没有确定,需要分类讨论.
巩固扩展
1.下列条件中,能判定△ABC∽△A'B'C'的是(
)
B
巩固扩展
2.
在△ABC和△A′B′C′中,
若∠B=∠B′,AB=12,BC=8,A′B′=6,
则当B′C′=______时,
△ABC∽△A′B′C′.
4
巩固扩展
3.
(1)如图1,请你增加一个条件:
,使△ABC∽△ACD.
AB
(
)
=
(
)
(
)
(2)如图2,请你增加一个条件:
,使△ABC∽△AED.
AB
(
)
=
(
)
(
)
AC
AC
AD
AE
AC
AD
巩固扩展
(3)如图3,请你增加一个条件:
使△ABC∽△ADE.
AB
(
)
=
(
)
(
)
(4)如图4,请你增加一个条件:
使△ABC∽△ADE.
AB
(
)
=
(
)
(
)
AD
AE
AC
AD
AE
AC
巩固扩展
(5)如图5,AC与BD不平行,请你增加一个条件
OA
(
)
=
(
)
(
)
使△AOC∽△DOB.
OC
OD
OB
巩固扩展
4.
如图,在△ABC中,
D,E分别是AB,AC上的点,
AB=7.8,BD=4.8,AC=6,AE=3.9,
试判断△ADE与△ABC是否相似,
某同学的解答如下:
巩固扩展
解:
∵
AB=AD+BD,而AB=7.8,BD=4.8,
∴
AD=7.8-4.8=3.
∵
∴
这两个三角形不相似.
你同意他的判断吗?请说明理由.
巩固扩展
解:
他的判断是错误的.
∵
AB=AD+BD,而AB=7.8,BD=4.8,
∴
AD=7.8-4.8=3.
∵
∴
又
∵
∠A=∠A,
∴
△ADE∽△ACB
.
巩固扩展
5.
如图,在4×4的方格图中,△ABC和△DEF都在边长为1的小正方形的顶点上,
求证:△ABC∽△DEF.
