北师大版七年级下册数学:2.1两条直线的位置关系垂直课件 (共19张PPT)
文档属性
| 名称 | 北师大版七年级下册数学:2.1两条直线的位置关系垂直课件 (共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-19 15:57:25 | ||
图片预览





文档简介
(共19张PPT)
2.1.2
特殊的相交
垂
直
)
α
a
b
b
b
b
b
)
α
情境引入
预习成果大展示
知识梳理
预习成果大展示
在你身边,找找相互垂直的线!
生活实例
1、下列四个条件中能判断两条直线垂直的有
(
)
①两条直线相交所成的四个角中有一个角是直角;
②两条直线相交所成的四个角相等;
③两条直线相交所成的四个角中有一组相邻的角相等;
④两条直线相交所成的四个角中有一组对顶角的和为180°。
A.4个
B.3个
C.2个
D.1个
A
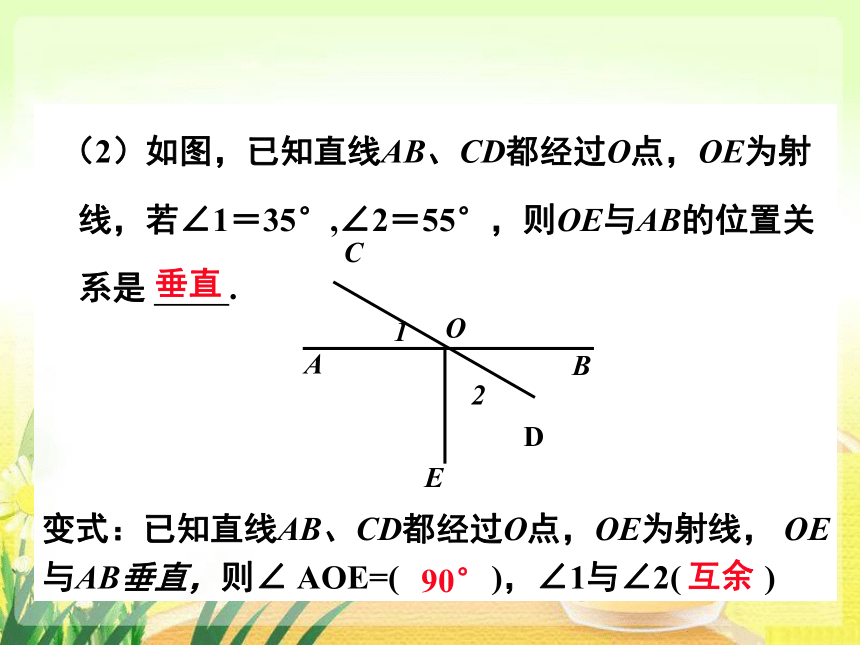
(2)如图,已知直线AB、CD都经过O点,OE为射
线,若∠1=35°,∠2=55°,则OE与AB的位置关
系是
.
垂直
变式:已知直线AB、CD都经过O点,OE为射线,
OE与AB垂直,则∠
AOE=(
),∠1与∠2(
)
90°
互余
预习成果大展示
(1)你能借助三角尺在下面画出两条互相垂
直的直线吗,你是怎么做到的?
(2)如果只有直尺,你能在下图中画出两条互相垂直的直线吗,你是怎么做到的?
(3)你能用折纸的方法折出互相垂直的直线吗?试试看!(记得带上你的作品哦!)
尝试解决
自主探究:平面内,过一点画一条直线的垂线,你可以画出来吗,你画出了多少条呢?
合作交流:组长有序组织组员发言,谈谈画法和结论。
?
自主探究
合作交流
小组合作要求
1.各组长有序地让组员讲解题目并说出自己的疑惑。
2.小组总结归纳:
你们小组出现了几种情况?
?
画法是什么?
?
结论是什么?
m
O
C
B
垂线段的长度就是这个点到直线的距离。
垂线段PO的长度就是跳远的成绩。
体育课上老师是怎样测量跳远成绩的?能说说说其中的道理吗?与同伴交流.
实际应用
P
O
实际应用
1、如图,
∠ACB=90°,则AC____BC;
∠CDB=90°,则
DC____AB
①线段AC、BC、CD中最短的是_____;
②若BC=4cm,AC=3cm,AB=5cm,那么点B到直线AC的距离等于_____,点A到直线BC的距离等于
_____
,A、B两点间的距离等于
_____.
有效练习
D
③你能求出点C到AB的距离吗?你是怎样做的?
⊥
⊥
CD
4cm
3cm
5cm
拓展练习
图1
图2
D
C
如图1所示:将一副三角板叠放在一起,使直角的顶点重合于点O
(1)∠AOD和∠BOC相等吗?说明理由.
(2)∠BOD和∠AOC在数量上也有特定的关系吗?我们来试试看:
①如果∠BOD=30°,
则∠AOD=(
),
∠BOC=(
),
∠AOC=(
),
∠BOD+∠AOC=(
)
②如果∠BOD=50°,
则∠AOD=(
),
∠BOC=(
),
∠AOC=(
),
∠BOD+∠AOC=(
).
③如果∠BOD=x°,则
∠BOD+∠AOC=(
)
(3)若将等腰的三角尺绕点O旋转到如图2的位置:
①∠AOD和∠BOC还相等吗?说明理由.
②∠AOC和∠BOD的以上关系还成立吗?说明理由
60°
60°
150°
180°
40°
40°
130°
180°
180°
如图所示:直角∠
BOD绕着直角∠AOC的顶点O进行旋转:
(1)如果∠DOC=30°,
则∠AOD=(
),
∠BOC=(
),
∠AOB=(
),
∠DOC+∠AOB=(
)
(2)如果∠DOC=50°,
则∠AOD=(
),
∠BOC=(
),
∠AOB=(
),
∠DOC+∠AOB=(
)
(3)大胆猜一下,不管这两个直角重叠多大的角,
∠DOC+∠AOB=(
)
(4)那如果这两个直角不重叠了呢?∠DOC+∠AOB=(
)
拓展练习
60°
60°
150°
180°
40°
40°
130°
180°
180°
180°
1、这节课我学会了
…
…
2、我会用它
…
…
3、我还感到疑惑的是
…
…
课堂小结
2.1.2
特殊的相交
垂
直
)
α
a
b
b
b
b
b
)
α
情境引入
预习成果大展示
知识梳理
预习成果大展示
在你身边,找找相互垂直的线!
生活实例
1、下列四个条件中能判断两条直线垂直的有
(
)
①两条直线相交所成的四个角中有一个角是直角;
②两条直线相交所成的四个角相等;
③两条直线相交所成的四个角中有一组相邻的角相等;
④两条直线相交所成的四个角中有一组对顶角的和为180°。
A.4个
B.3个
C.2个
D.1个
A
(2)如图,已知直线AB、CD都经过O点,OE为射
线,若∠1=35°,∠2=55°,则OE与AB的位置关
系是
.
垂直
变式:已知直线AB、CD都经过O点,OE为射线,
OE与AB垂直,则∠
AOE=(
),∠1与∠2(
)
90°
互余
预习成果大展示
(1)你能借助三角尺在下面画出两条互相垂
直的直线吗,你是怎么做到的?
(2)如果只有直尺,你能在下图中画出两条互相垂直的直线吗,你是怎么做到的?
(3)你能用折纸的方法折出互相垂直的直线吗?试试看!(记得带上你的作品哦!)
尝试解决
自主探究:平面内,过一点画一条直线的垂线,你可以画出来吗,你画出了多少条呢?
合作交流:组长有序组织组员发言,谈谈画法和结论。
?
自主探究
合作交流
小组合作要求
1.各组长有序地让组员讲解题目并说出自己的疑惑。
2.小组总结归纳:
你们小组出现了几种情况?
?
画法是什么?
?
结论是什么?
m
O
C
B
垂线段的长度就是这个点到直线的距离。
垂线段PO的长度就是跳远的成绩。
体育课上老师是怎样测量跳远成绩的?能说说说其中的道理吗?与同伴交流.
实际应用
P
O
实际应用
1、如图,
∠ACB=90°,则AC____BC;
∠CDB=90°,则
DC____AB
①线段AC、BC、CD中最短的是_____;
②若BC=4cm,AC=3cm,AB=5cm,那么点B到直线AC的距离等于_____,点A到直线BC的距离等于
_____
,A、B两点间的距离等于
_____.
有效练习
D
③你能求出点C到AB的距离吗?你是怎样做的?
⊥
⊥
CD
4cm
3cm
5cm
拓展练习
图1
图2
D
C
如图1所示:将一副三角板叠放在一起,使直角的顶点重合于点O
(1)∠AOD和∠BOC相等吗?说明理由.
(2)∠BOD和∠AOC在数量上也有特定的关系吗?我们来试试看:
①如果∠BOD=30°,
则∠AOD=(
),
∠BOC=(
),
∠AOC=(
),
∠BOD+∠AOC=(
)
②如果∠BOD=50°,
则∠AOD=(
),
∠BOC=(
),
∠AOC=(
),
∠BOD+∠AOC=(
).
③如果∠BOD=x°,则
∠BOD+∠AOC=(
)
(3)若将等腰的三角尺绕点O旋转到如图2的位置:
①∠AOD和∠BOC还相等吗?说明理由.
②∠AOC和∠BOD的以上关系还成立吗?说明理由
60°
60°
150°
180°
40°
40°
130°
180°
180°
如图所示:直角∠
BOD绕着直角∠AOC的顶点O进行旋转:
(1)如果∠DOC=30°,
则∠AOD=(
),
∠BOC=(
),
∠AOB=(
),
∠DOC+∠AOB=(
)
(2)如果∠DOC=50°,
则∠AOD=(
),
∠BOC=(
),
∠AOB=(
),
∠DOC+∠AOB=(
)
(3)大胆猜一下,不管这两个直角重叠多大的角,
∠DOC+∠AOB=(
)
(4)那如果这两个直角不重叠了呢?∠DOC+∠AOB=(
)
拓展练习
60°
60°
150°
180°
40°
40°
130°
180°
180°
180°
1、这节课我学会了
…
…
2、我会用它
…
…
3、我还感到疑惑的是
…
…
课堂小结
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
