人教版九年级数学下册 27.2.1 相似三角形的判定第三课时 两角分别相等的两个三角形相似课件(30张ppt)
文档属性
| 名称 | 人教版九年级数学下册 27.2.1 相似三角形的判定第三课时 两角分别相等的两个三角形相似课件(30张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-19 11:28:31 | ||
图片预览










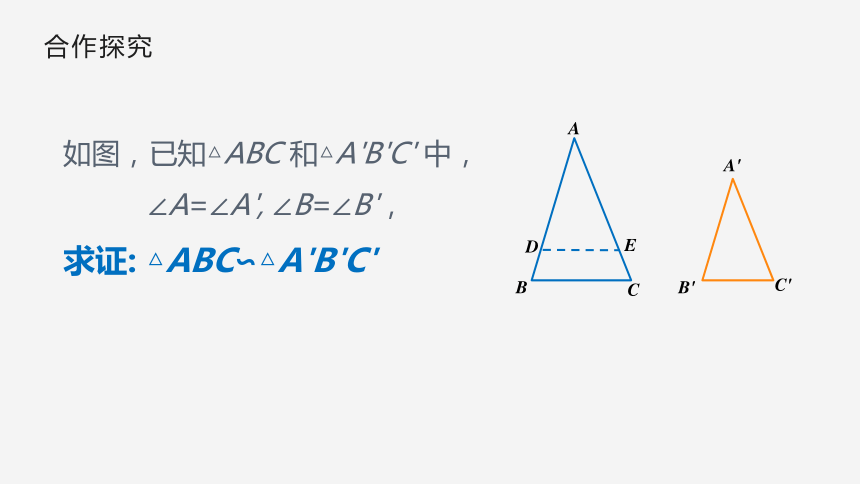

文档简介
(共30张PPT)
27.2.1
相似三角形的判定
第3课时
两角分别相等的两个
三角形相似
27
相
似
学习目标
教学分析
1.掌握相似三角形的判定定理:“如果一个三角形的两个角
与另一个三角形的两个角对应相等,那么这两个三角形相似”.
2.了解“斜边的比等于一组直角边的比的两相直角三角形相似”.
3.会进行简单的证明、计算.
导入新课
根据三角形全等的定义
两个三角形中有3个角和3条边都对应相等(将3角3边称作三角形的6个元素,即三角形的6个元素都相等),这两个三角形全等.
但在探索三角形全等的条件时,是从两个三角形中有1个元素对应相等开始,逐渐增多条件,来考查三角形是否全等.
导入新课
这节课,我们就仿照探索三角形全等的条件
的思路来探索三角形相似的条件.
先从两个三角形只有1个角对应相等开始,
探索两个三角形相似的条件.
合作探究
探究点一
两角对应相等
与三角形相似及其应用
合作探究
观察两副三角尺如图,其中同样角度(30°与60°,或45°与45°)的
两个三角尺大小可能不同,但它们看起来是相似的.
一般地,如果两个三角形有两组对应角相等,它们一定相似吗?
一定相似
合作探究
探究:
作△ABC
和△A'B'C',
使得∠A=∠A',∠B=∠B',
这时它们的第三个角满足∠C=∠C
'吗?
分别度量这两个三角形的边长,
计算
,
你有什么发现?
A
B
C
A'
B'
C'
合作探究
解:
满足:∠C
=
∠C'
△ABC∽△A'B'C'
合作探究
探究:
把你的结果与邻座的同学比较,你们的结论一样吗?
△ABC
和△A'B'C'
相似吗?
答:一样,△ABC
和△A'B'C'
相似。
合作探究
得到判定两个三角形相似的又一个简便方法:
两角分别相等的两个三角形
相似.
合作探究
如图,已知△ABC
和△A'B'C'
中,
∠A=∠A',
∠B=∠B',
求证:
△ABC∽△A'B'C'
A
B
C
D
E
A'
B'
C'
合作探究
证明:
在△ABC
的边AB(或延长线)上,截取AD=A'B',
过点D
作DE//BC,交AC
于点E,
则有△ADE∽△ABC.
∵
∠ADE=∠B
,
∠B=∠B'
∴
∠ADE=∠B'
又
∵
∠A=∠A'
,
AD=A'B'
∴
△ADE
≌△A'B'C'
∴
△A'B'C'∽△ABC
合作探究
如图27.2-11,Rt△ABC中,∠C=90°,AB=10,AC=8.
E是AC上一点,AE=5,ED⊥AB,垂足为D,求AD的长。
图27.2-11
∵
ED⊥AB,
解:
∴
∠EDA=90°
又
∠C=90°,∠A=∠A,
∴
∴
合作探究
1.如图,△ABC内接于⊙O,
∠BAC的平分线交⊙O于点D,
交BC于点E,连接BD.
(1)请你找出图中所有的相似三角形;
解:
△DBE∽△DAB;
△DBE∽△CAE;
△ABD∽△AEC;
针对训练
1
合作探究
(2)请选择其中的一对相似三角形予以证明.
解:
选择△ABD∽△AEC.
∵
DA是∠BAC的平分线,
∴
∠BAD=∠CAE.
又
∵∠D=∠C,∴△ABD∽△AEC.
2.在上题条件下,若DE=3,EA=7,则BD=______.
合作探究
探究点二
两个直角三角形的相似
合作探究
阅读教材第36页“思考”及下面的证明过程.
思考:如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.
图中有哪几对相似三角形?为什么?
了解:满足斜边的比等于一组直角边的比的两个直角三角形相似.
合作探究
分析
∵
CD⊥AB,
∴
∠CDB=90°.
∴
∠B+∠BCD=90°.
又
∵
∠ACB=90°,
∴
∠B+∠A=90°.
∴
∠BCD=∠A.
在
△ABC和△CBD中,∵
∠ACB=∠CDB=90°,∠BCD=∠A,
∴
△ABC∽△CBD.
合作探究
请你再找出其他的几对相似三角形:
△ABC∽△ACD,
△CBD∽△ACD
合作探究
小组讨论
1
如何根据题目特点
灵活选用本节所学相似三角形的判定方法?
合作探究
反思小结
验证两三角形相似,若已具备一组角对应相等,则应先考虑“两角
对应相等的两个三角形相似”这一判定方法,而找等角时常用到
公共角、对顶角、等角(或同角)的余角相等等一些隐含条件.
判定直角三角形相似时,可以用其相似独有的判定方法,也可以用一般三角形相似的判定方法.不过,更多的时候是用两角相等来证.
合作探究
3.
如图,在矩形ABCD中,DE⊥AC于E,
则△ABC∽△
,△ABC∽△
,△ABC∽△
.
CED
DEA
CDA
针对训练
2
合作探究
概念、
性质
1.两角分别相等的两个三角形_______.
2.斜边的比等于一组直角边的比的两组直角三角形_______.
方法、规律
如左图,∠BPD=∠BAP=∠DCP=α,则△ABP∽△CPD.
实际解题中,遇到较多的是α等于45°,60°,90°
三种情况。
如果AB//CD,那么
.
如果AB//CD,那么△ABP∽△DPC.
所以
相似
相似
合作探究
易错点
对于上面基本图2,如果AB//CD,
并不能直接证得
和
.
巩固拓展
1.下列结论:
①所有的等腰三角形都相似,
②有一个角是80°的两个等腰三角形相似,
③有一个角是100°的两个等腰三角形相似,
④有一个角相等的两个等腰三角形相似,其中正确的有(
)
A.1个
B.2个
C.3个
D.4个
A
巩固拓展
2.如图1,在梯形ABCD中,AD∥
BC,对角线AC,BD相交于点O,若AD=1,BC=3,则
的值为( )
A.
B.
C.
D.
B
巩固拓展
(1)
若AD=8,BD=2,则CD=
;
(2)
若BD=4,AB=9,则BC=
;
(3)
若AD=2,AB=3,则AC=
;
(4)
若CD=8,BD=4,则AD=
.
(5)
若AB=5,AC=4,则CD=
.
3.如图,在Rt△ABC中,∠ACB=90°,
CD是斜边AB上的高.
4
6
16
2.4
巩固拓展
4.
(1)如图1,请你增加一个条件:
∠
=∠
(或∠
=∠
),
使△ABC∽△ACD.
(2)如图2,请你增加一个条件:
∠
=∠
(或∠
=∠
),使△ABC∽△AED.
ACB
ADC
ABC
ACD
ACB
ADE
ABC
AED
巩固拓展
5.
(1)如图3,
已知AC=6,AD=4,
∠B=∠ACD,
求AB的长.
∴
,
即
AC2=AD·AB,
AD
AC
解:
在△ABC与△ACD中,
∵
∠____=∠A,∠____=∠ACD,
∴
∠ABC∽∠________.
A
B
ACD
∴
62
=4·AB,
∴
AB=___.
9
巩固拓展
(2)如图4,已知AC=6,AD=4,AE=3,∠B=∠AED,
求AB的长.
解:
在△ABC与△AED中,
∵
∠____=∠A,∠____=∠AED,
∴△ABC∽△________.
∴
,
即
AE·____=AD·AB,
∴
____×____=2·AB,
∴
AB=____.
A
B
ADE
AB
AE
AC
3
6
9
27.2.1
相似三角形的判定
第3课时
两角分别相等的两个
三角形相似
27
相
似
学习目标
教学分析
1.掌握相似三角形的判定定理:“如果一个三角形的两个角
与另一个三角形的两个角对应相等,那么这两个三角形相似”.
2.了解“斜边的比等于一组直角边的比的两相直角三角形相似”.
3.会进行简单的证明、计算.
导入新课
根据三角形全等的定义
两个三角形中有3个角和3条边都对应相等(将3角3边称作三角形的6个元素,即三角形的6个元素都相等),这两个三角形全等.
但在探索三角形全等的条件时,是从两个三角形中有1个元素对应相等开始,逐渐增多条件,来考查三角形是否全等.
导入新课
这节课,我们就仿照探索三角形全等的条件
的思路来探索三角形相似的条件.
先从两个三角形只有1个角对应相等开始,
探索两个三角形相似的条件.
合作探究
探究点一
两角对应相等
与三角形相似及其应用
合作探究
观察两副三角尺如图,其中同样角度(30°与60°,或45°与45°)的
两个三角尺大小可能不同,但它们看起来是相似的.
一般地,如果两个三角形有两组对应角相等,它们一定相似吗?
一定相似
合作探究
探究:
作△ABC
和△A'B'C',
使得∠A=∠A',∠B=∠B',
这时它们的第三个角满足∠C=∠C
'吗?
分别度量这两个三角形的边长,
计算
,
你有什么发现?
A
B
C
A'
B'
C'
合作探究
解:
满足:∠C
=
∠C'
△ABC∽△A'B'C'
合作探究
探究:
把你的结果与邻座的同学比较,你们的结论一样吗?
△ABC
和△A'B'C'
相似吗?
答:一样,△ABC
和△A'B'C'
相似。
合作探究
得到判定两个三角形相似的又一个简便方法:
两角分别相等的两个三角形
相似.
合作探究
如图,已知△ABC
和△A'B'C'
中,
∠A=∠A',
∠B=∠B',
求证:
△ABC∽△A'B'C'
A
B
C
D
E
A'
B'
C'
合作探究
证明:
在△ABC
的边AB(或延长线)上,截取AD=A'B',
过点D
作DE//BC,交AC
于点E,
则有△ADE∽△ABC.
∵
∠ADE=∠B
,
∠B=∠B'
∴
∠ADE=∠B'
又
∵
∠A=∠A'
,
AD=A'B'
∴
△ADE
≌△A'B'C'
∴
△A'B'C'∽△ABC
合作探究
如图27.2-11,Rt△ABC中,∠C=90°,AB=10,AC=8.
E是AC上一点,AE=5,ED⊥AB,垂足为D,求AD的长。
图27.2-11
∵
ED⊥AB,
解:
∴
∠EDA=90°
又
∠C=90°,∠A=∠A,
∴
∴
合作探究
1.如图,△ABC内接于⊙O,
∠BAC的平分线交⊙O于点D,
交BC于点E,连接BD.
(1)请你找出图中所有的相似三角形;
解:
△DBE∽△DAB;
△DBE∽△CAE;
△ABD∽△AEC;
针对训练
1
合作探究
(2)请选择其中的一对相似三角形予以证明.
解:
选择△ABD∽△AEC.
∵
DA是∠BAC的平分线,
∴
∠BAD=∠CAE.
又
∵∠D=∠C,∴△ABD∽△AEC.
2.在上题条件下,若DE=3,EA=7,则BD=______.
合作探究
探究点二
两个直角三角形的相似
合作探究
阅读教材第36页“思考”及下面的证明过程.
思考:如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.
图中有哪几对相似三角形?为什么?
了解:满足斜边的比等于一组直角边的比的两个直角三角形相似.
合作探究
分析
∵
CD⊥AB,
∴
∠CDB=90°.
∴
∠B+∠BCD=90°.
又
∵
∠ACB=90°,
∴
∠B+∠A=90°.
∴
∠BCD=∠A.
在
△ABC和△CBD中,∵
∠ACB=∠CDB=90°,∠BCD=∠A,
∴
△ABC∽△CBD.
合作探究
请你再找出其他的几对相似三角形:
△ABC∽△ACD,
△CBD∽△ACD
合作探究
小组讨论
1
如何根据题目特点
灵活选用本节所学相似三角形的判定方法?
合作探究
反思小结
验证两三角形相似,若已具备一组角对应相等,则应先考虑“两角
对应相等的两个三角形相似”这一判定方法,而找等角时常用到
公共角、对顶角、等角(或同角)的余角相等等一些隐含条件.
判定直角三角形相似时,可以用其相似独有的判定方法,也可以用一般三角形相似的判定方法.不过,更多的时候是用两角相等来证.
合作探究
3.
如图,在矩形ABCD中,DE⊥AC于E,
则△ABC∽△
,△ABC∽△
,△ABC∽△
.
CED
DEA
CDA
针对训练
2
合作探究
概念、
性质
1.两角分别相等的两个三角形_______.
2.斜边的比等于一组直角边的比的两组直角三角形_______.
方法、规律
如左图,∠BPD=∠BAP=∠DCP=α,则△ABP∽△CPD.
实际解题中,遇到较多的是α等于45°,60°,90°
三种情况。
如果AB//CD,那么
.
如果AB//CD,那么△ABP∽△DPC.
所以
相似
相似
合作探究
易错点
对于上面基本图2,如果AB//CD,
并不能直接证得
和
.
巩固拓展
1.下列结论:
①所有的等腰三角形都相似,
②有一个角是80°的两个等腰三角形相似,
③有一个角是100°的两个等腰三角形相似,
④有一个角相等的两个等腰三角形相似,其中正确的有(
)
A.1个
B.2个
C.3个
D.4个
A
巩固拓展
2.如图1,在梯形ABCD中,AD∥
BC,对角线AC,BD相交于点O,若AD=1,BC=3,则
的值为( )
A.
B.
C.
D.
B
巩固拓展
(1)
若AD=8,BD=2,则CD=
;
(2)
若BD=4,AB=9,则BC=
;
(3)
若AD=2,AB=3,则AC=
;
(4)
若CD=8,BD=4,则AD=
.
(5)
若AB=5,AC=4,则CD=
.
3.如图,在Rt△ABC中,∠ACB=90°,
CD是斜边AB上的高.
4
6
16
2.4
巩固拓展
4.
(1)如图1,请你增加一个条件:
∠
=∠
(或∠
=∠
),
使△ABC∽△ACD.
(2)如图2,请你增加一个条件:
∠
=∠
(或∠
=∠
),使△ABC∽△AED.
ACB
ADC
ABC
ACD
ACB
ADE
ABC
AED
巩固拓展
5.
(1)如图3,
已知AC=6,AD=4,
∠B=∠ACD,
求AB的长.
∴
,
即
AC2=AD·AB,
AD
AC
解:
在△ABC与△ACD中,
∵
∠____=∠A,∠____=∠ACD,
∴
∠ABC∽∠________.
A
B
ACD
∴
62
=4·AB,
∴
AB=___.
9
巩固拓展
(2)如图4,已知AC=6,AD=4,AE=3,∠B=∠AED,
求AB的长.
解:
在△ABC与△AED中,
∵
∠____=∠A,∠____=∠AED,
∴△ABC∽△________.
∴
,
即
AE·____=AD·AB,
∴
____×____=2·AB,
∴
AB=____.
A
B
ADE
AB
AE
AC
3
6
9
