人教版九年级数学下册 27.2.2 相似三角形的性质课件(21张ppt)
文档属性
| 名称 | 人教版九年级数学下册 27.2.2 相似三角形的性质课件(21张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-19 00:00:00 | ||
图片预览






文档简介
(共21张PPT)
27
27.2.2
相似三角形的性质
相
似
学习目标
教学分析
1.经历在具体问题中探究反比例函数应用的过程,体会反比例函数作为一种数学模型的意义。
2.利用反比例函数的知识分析和解决实际问题。
3.渗透数形结合思想,提高用函数观点解决问题的能力。
导入新课
1.相似三角形有哪些性质?
相似多边形对应边的比叫做相似比.
2.什么叫做相似比?
答:
相似三角形的性质有:
①相似三角形的对应角相等;
②相似三角形的对应边的比等于相似比.
答:
合作探究
知识点一
相似三角形对应高、中线、角平分线的比
合作探究
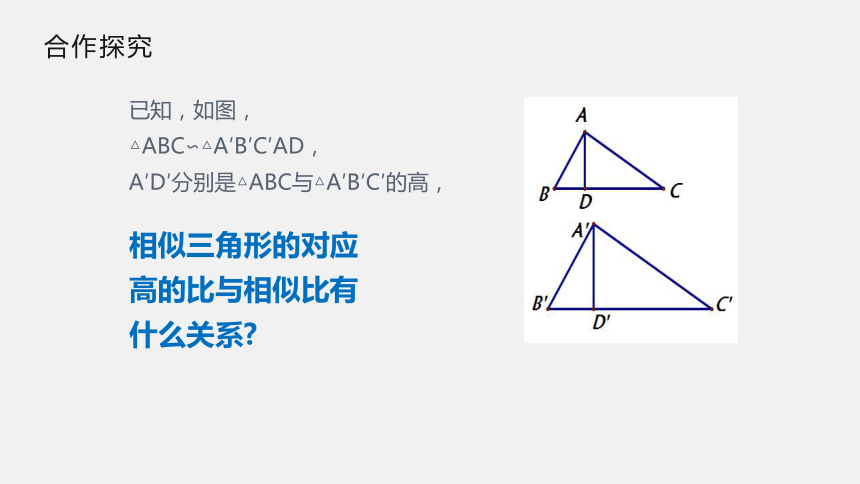
已知,如图,
△ABC∽△A′B′C′AD,
A′D′分别是△ABC与△A′B′C′的高,
相似三角形的对应高的比与相似比有什么关系?
合作探究
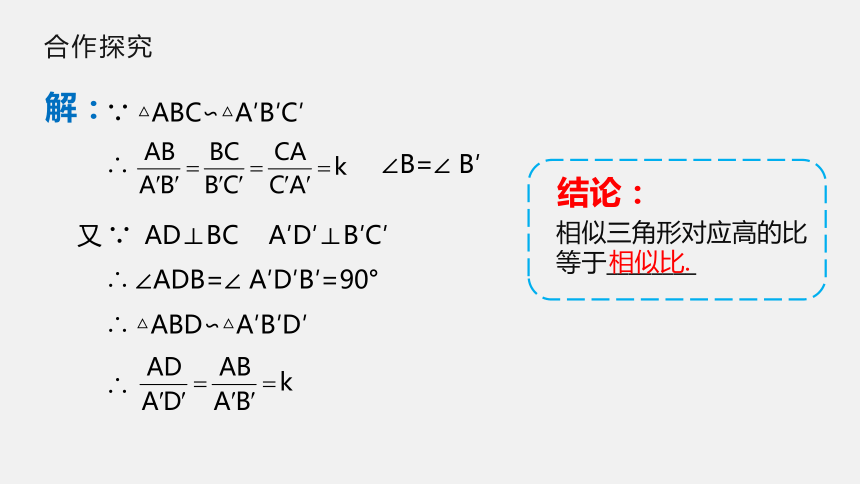
解:
∵
△ABC∽△A′B′C′
∴
∠B=∠
B′
又
∵
AD⊥BC
A′D′⊥B′C′
∴
∠ADB=∠
A′D′B′=90°
∴
△ABD∽△A′B′D′
∴
结论:
相似三角形对应高的比
等于________
相似比.
合作探究
知识点二
相似三角形的周长比
合作探究
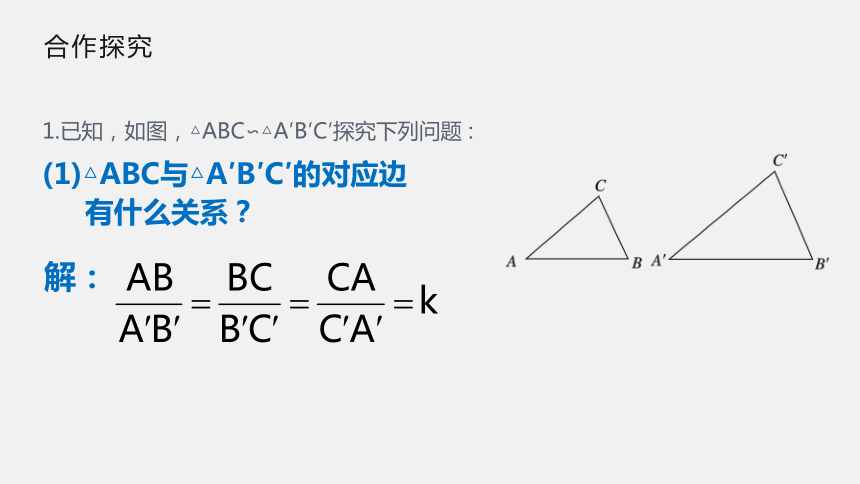
1.已知,如图,△ABC∽△A′B′C′探究下列问题
:
(1)△ABC与△A′B′C′的对应边
有什么关系?
解:
合作探究
(2)若
,则
的比值是否等于k
?
解:
∵△ABC∽△A′B′C′,且相似比为k
∴
∴
∴
合作探究
相似三角形周长的比等于________.
相似多边形周长的比等于_______.
相似比
相似比
合作探究
练一练
1.如果把一个三角形各边同时扩大为原来的5倍,那么它的周长也扩大为
原来的____倍.
5
2.如图,点D、E分别是△ABC边AB、AC上的点,
且DE∥BC,BD=2AD,
那么△ADE的周长︰
△ABC的周长=_______
.
1:3
合作探究
结论:
相似三角形对应
边上的中线,
对应角的平分线的比等于_______________
相似比的平方.
相似三角形对应边上的中线,
对应角的平分线的比值与相似比
有什么关系?
相等。
合作探究
(3)若
=k
,则
的比值与k
有什么关系?
等于k2
结论:
相似三角形面积的比等于_______________
相似比的平方.
合作探究
用类似的方法,可以把两个相似多边形
分成若干对相似三角形,因此可以得出:
相似多边形面积的比等于_______________.
相似比的平方
合作探究
练一练
1.两个相似三角形对应高的长分别是6cm和18cm,
若较大三角形的周长是42cm,面积是12cm2,
则较小三角形的周长为____cm,面积为____cm2。
14
合作探究
2.在△ABC中,DE∥BC,EF∥AB,已知△ADE和△EFC的面积分别为4和9,
求△ABC的面积.
解:
∵
DE∥BC,EF∥AB
∴
∠AED=∠C,∠A=∠CEF
∴
△ADE∽△EFC
而S△ADE=4,S△EFC=9
合作探究
解:
∴
∴
∴
∴
∴
S△ABC=
课堂小结
3.学习反思:____________________.
1.相似三角形周长、对应高、对应中线、
对应角平分线的比等于__________.
2.相似三角形面积的比等于___________________.
相似比
相似比的平方
强化训练
1.连接三角形两边中点的线段把三角形截成的一个小三角形
与原三角形的周长比等于
,面积比等于
.
2.如果两个相似三角形面积的比为3∶5
,
那么它们的相似比为_________,周长的比为_________.
:
:
强化训练
3.在一张复印出来的纸上,一个多边形的一条边由原图中的2cm变成了6cm,
这次复印的放缩比例是多少?这个多边形的面积有什么变化?
解:
∵
比例是6∶2
=
3∶1,
∴
这次复印的放缩比例是300%.
又
∵
面积比是9∶1,
∴
这个多边形的面积扩大到9倍.
强化训练
4.
如图,在正方形网格上有△A1B1C1和△A2B2C2,这两个三角形相似吗?
如果相似,求出△A1B1C1和△A2B2C2的面积比.
解:
相似
(△A1B1C1∽△A2B2C2
)
∵
∴
27
27.2.2
相似三角形的性质
相
似
学习目标
教学分析
1.经历在具体问题中探究反比例函数应用的过程,体会反比例函数作为一种数学模型的意义。
2.利用反比例函数的知识分析和解决实际问题。
3.渗透数形结合思想,提高用函数观点解决问题的能力。
导入新课
1.相似三角形有哪些性质?
相似多边形对应边的比叫做相似比.
2.什么叫做相似比?
答:
相似三角形的性质有:
①相似三角形的对应角相等;
②相似三角形的对应边的比等于相似比.
答:
合作探究
知识点一
相似三角形对应高、中线、角平分线的比
合作探究
已知,如图,
△ABC∽△A′B′C′AD,
A′D′分别是△ABC与△A′B′C′的高,
相似三角形的对应高的比与相似比有什么关系?
合作探究
解:
∵
△ABC∽△A′B′C′
∴
∠B=∠
B′
又
∵
AD⊥BC
A′D′⊥B′C′
∴
∠ADB=∠
A′D′B′=90°
∴
△ABD∽△A′B′D′
∴
结论:
相似三角形对应高的比
等于________
相似比.
合作探究
知识点二
相似三角形的周长比
合作探究
1.已知,如图,△ABC∽△A′B′C′探究下列问题
:
(1)△ABC与△A′B′C′的对应边
有什么关系?
解:
合作探究
(2)若
,则
的比值是否等于k
?
解:
∵△ABC∽△A′B′C′,且相似比为k
∴
∴
∴
合作探究
相似三角形周长的比等于________.
相似多边形周长的比等于_______.
相似比
相似比
合作探究
练一练
1.如果把一个三角形各边同时扩大为原来的5倍,那么它的周长也扩大为
原来的____倍.
5
2.如图,点D、E分别是△ABC边AB、AC上的点,
且DE∥BC,BD=2AD,
那么△ADE的周长︰
△ABC的周长=_______
.
1:3
合作探究
结论:
相似三角形对应
边上的中线,
对应角的平分线的比等于_______________
相似比的平方.
相似三角形对应边上的中线,
对应角的平分线的比值与相似比
有什么关系?
相等。
合作探究
(3)若
=k
,则
的比值与k
有什么关系?
等于k2
结论:
相似三角形面积的比等于_______________
相似比的平方.
合作探究
用类似的方法,可以把两个相似多边形
分成若干对相似三角形,因此可以得出:
相似多边形面积的比等于_______________.
相似比的平方
合作探究
练一练
1.两个相似三角形对应高的长分别是6cm和18cm,
若较大三角形的周长是42cm,面积是12cm2,
则较小三角形的周长为____cm,面积为____cm2。
14
合作探究
2.在△ABC中,DE∥BC,EF∥AB,已知△ADE和△EFC的面积分别为4和9,
求△ABC的面积.
解:
∵
DE∥BC,EF∥AB
∴
∠AED=∠C,∠A=∠CEF
∴
△ADE∽△EFC
而S△ADE=4,S△EFC=9
合作探究
解:
∴
∴
∴
∴
∴
S△ABC=
课堂小结
3.学习反思:____________________.
1.相似三角形周长、对应高、对应中线、
对应角平分线的比等于__________.
2.相似三角形面积的比等于___________________.
相似比
相似比的平方
强化训练
1.连接三角形两边中点的线段把三角形截成的一个小三角形
与原三角形的周长比等于
,面积比等于
.
2.如果两个相似三角形面积的比为3∶5
,
那么它们的相似比为_________,周长的比为_________.
:
:
强化训练
3.在一张复印出来的纸上,一个多边形的一条边由原图中的2cm变成了6cm,
这次复印的放缩比例是多少?这个多边形的面积有什么变化?
解:
∵
比例是6∶2
=
3∶1,
∴
这次复印的放缩比例是300%.
又
∵
面积比是9∶1,
∴
这个多边形的面积扩大到9倍.
强化训练
4.
如图,在正方形网格上有△A1B1C1和△A2B2C2,这两个三角形相似吗?
如果相似,求出△A1B1C1和△A2B2C2的面积比.
解:
相似
(△A1B1C1∽△A2B2C2
)
∵
∴
