北师大版八年级下册数学4.2提公因式法——公因式为多项式课件(共17张PPT)
文档属性
| 名称 | 北师大版八年级下册数学4.2提公因式法——公因式为多项式课件(共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 140.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-20 08:50:43 | ||
图片预览






文档简介
(共17张PPT)
北师版
八年级
下册
第四章
因式分解
2
公因式为多项式的提公因式法
复习旧知
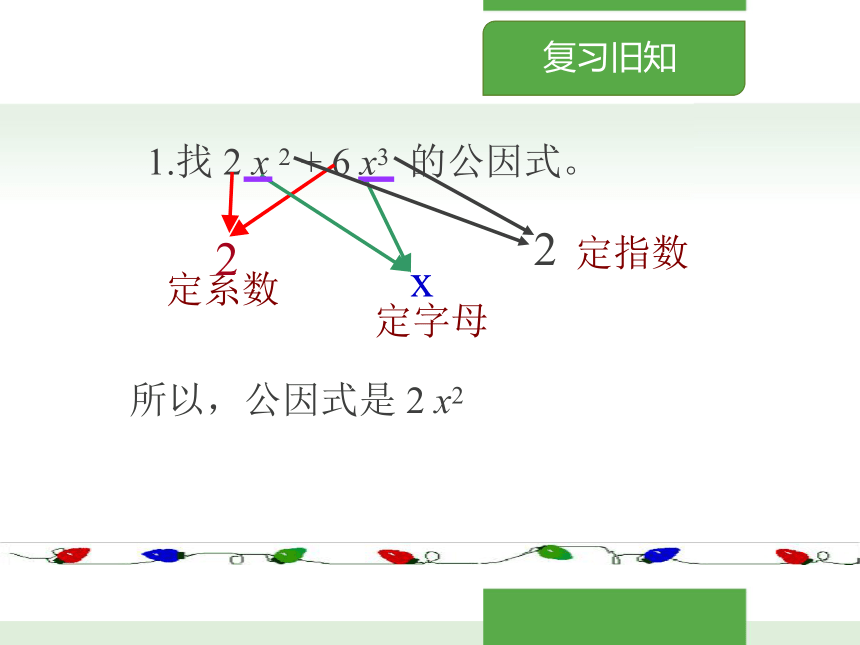
1.定系数:是多项式各项_____________
;
2.定字母:字母取多项式各项中都含有的____________;
3.定指数:相同字母的指数取各项中最小的一个,即
_________;
4.多项式的第一项系数为负数时,
.
提公因式法因式分解:
系数的最大公约数
相同的字母
最低次幂
先提取“-”号,注意多项式的各项变号
写成乘积的形式为公因式
1.找
2
x
2
+
6
x3
的公因式。
定系数
2
定字母
x
定指数
2
所以,公因式是
2
x2
复习旧知
例题演示1
(1)
a(x-3)+2b(x-3)
例2、把下列各式分解因式
(2)
y(x+1)+y2
(x+1)2
解:a(x-3)+2b(x-3)
=(x-3)
(a+2b)
解:y(x+1)+y2
(x+1)2
=y(x+1)
[1+y(x+1)]
=y(x+1)
(xy+y+1)
讲授新课
把下列各式分解因式
(1)
7(a-1)+x(a-1)
(2)
2(m-n)2-m(m-n)
(3)
m(a2+b2)+n
(a2+b2)
(4)
(2a+b)(2a-3b)-3a(2a+b)
练习
讲授新课
请在下列各式等号右边填入“+”或“-”号,使等式成立.
(1)
2-a=
(a-2)
(2)
y-x=
(x-y)
(3)
b+a=
(a+b)
-
(6)-m-n=
(m+n)
(5)
–s2+t2=
(s2-t2)
(4)
(b-a)2=
(a-b)2
-
+
+
-
-
做一做
规律总结
(1)a-b
与
-a+b
互为相反数.
(a-b)n
=
(b-a)n
(n是偶数)
(a-b)n
=
-(b-a)n
(n是奇数)
(3)
a+b与b+a
互为相同数.
(a+b)n
=
(b+a)n
(n是整数)
(2)a+b
与
-a-b互为相反数.
(-a-b)n
=
(a+b)n
(n是偶数)
(-a-b)n
=
-(a+b)n
(n是奇数)
讲授新课
例3、把下列各式分解因式
(1)a(x-y)+b(y-x)
(2)6(m-n)3-12(n-m)2
解:a(x-y)+b(y-x)
=a(x-y)
-b(x-y)
=
(x-y)(a-b)
解:6(m-n)3-12(n-m)2
=6(m-n)3
-12[-(m-n)]2
=
6(m-n)3-12(m-n)2
=6(m-n)2(m-n-2)
例题演示2
讲授新课
(1)3(a-b)2+6(b-a)
(2)x(x-y)2-y(y-x)2
(3)18(a-b)3-12b(b-a)2
(4)x(x+y)(x-y)
-x
(x+y)2
练习
解:原式=(2y+x)2[(2x-(x-2y)]
=(2y+x)2(x+2y)
=(2y+x)3
当x=2,y=3时
原式=(2×3+2)3
=83
=512
当x=2,y=3时,
注意解题格式
①将原式化简
②当。。。时,
代人最简式中计算。
提升练习
课后小结
谈谈本节课你有哪些收获?
(2)
5x(a-b)2+10y(b-a)2
)
3
(
2
3
)
(
12
)
(
6
m
n
n
m
-
-
-
)
(
)
(
)
1
(
x
y
b
y
x
a
-
-
-
7.把下列各式分解因式:
(4)
a(a+b)(a-b)-a(a+b)2
(5)
mn(m+n)-m(n+m)2
(6)
2(a-3)2-a+3
(7)
a(x-a)+b(a-x)-c(x-a)
讲授新课
1.判断下列各式是否正确?
(1)
(y-x)2
=
-(x-y)2
(2)
(3+2x)3
=
-(2x+3)3
(3)
a-2b
=
-(-2b+a)
(4)
-a+b
=
-(a+b)
(5)
(a-b)(x-2y)
=
(b-a)(2y-x)
否
否
否
否
对
随堂练习
2.把
a(x-3)+2b(x-3)
分解因式.
解:
a(x-3)+2b(x-3) =(x-3)(a+2b)
分析:
多项式可看成
a(x-3)
与
2b(x-3)
两项。
公因式为x-3
随堂练习
3.
把a(x-y)+b(y-x)分解因式.
解:
a(x-y)+b(y-x)
=a(x-y)-b(x-y) =(x-y)(a-b)
分析:多项式可看成a(x-y)与+b(y-x)两项。其中X-y与y-x互为相反数,可将+b(y-x)变为-b(x-y),
则a(x-y)与-b(x-y)
公因式为
x-y
随堂练习
4.
把6(m-n)3-12(n-m)2分解因式.
分析:其中(m-n)与(n-m)互为相反数.可将-12(n-m)
2变为-12(m-n)2,则6(m-n)3与-12(m-n)2
公因式为6(m-n)2
随堂练习
5.把6(x+y)(y-x)2-9(x-y)3分解因式.
解:
6(x+y)(y-x)2-
9(x-y)3
=
6(x+y)(x-y)2-
9(x-y)3
=
3(x-y)2[2(x+y)-3(x-y)]
=
3(x-y)2(2x+2y-3x+3y)
=
3(x-y)2(-x+5y)
=3(x-y)2(5y-x)
随堂练习
北师版
八年级
下册
第四章
因式分解
2
公因式为多项式的提公因式法
复习旧知
1.定系数:是多项式各项_____________
;
2.定字母:字母取多项式各项中都含有的____________;
3.定指数:相同字母的指数取各项中最小的一个,即
_________;
4.多项式的第一项系数为负数时,
.
提公因式法因式分解:
系数的最大公约数
相同的字母
最低次幂
先提取“-”号,注意多项式的各项变号
写成乘积的形式为公因式
1.找
2
x
2
+
6
x3
的公因式。
定系数
2
定字母
x
定指数
2
所以,公因式是
2
x2
复习旧知
例题演示1
(1)
a(x-3)+2b(x-3)
例2、把下列各式分解因式
(2)
y(x+1)+y2
(x+1)2
解:a(x-3)+2b(x-3)
=(x-3)
(a+2b)
解:y(x+1)+y2
(x+1)2
=y(x+1)
[1+y(x+1)]
=y(x+1)
(xy+y+1)
讲授新课
把下列各式分解因式
(1)
7(a-1)+x(a-1)
(2)
2(m-n)2-m(m-n)
(3)
m(a2+b2)+n
(a2+b2)
(4)
(2a+b)(2a-3b)-3a(2a+b)
练习
讲授新课
请在下列各式等号右边填入“+”或“-”号,使等式成立.
(1)
2-a=
(a-2)
(2)
y-x=
(x-y)
(3)
b+a=
(a+b)
-
(6)-m-n=
(m+n)
(5)
–s2+t2=
(s2-t2)
(4)
(b-a)2=
(a-b)2
-
+
+
-
-
做一做
规律总结
(1)a-b
与
-a+b
互为相反数.
(a-b)n
=
(b-a)n
(n是偶数)
(a-b)n
=
-(b-a)n
(n是奇数)
(3)
a+b与b+a
互为相同数.
(a+b)n
=
(b+a)n
(n是整数)
(2)a+b
与
-a-b互为相反数.
(-a-b)n
=
(a+b)n
(n是偶数)
(-a-b)n
=
-(a+b)n
(n是奇数)
讲授新课
例3、把下列各式分解因式
(1)a(x-y)+b(y-x)
(2)6(m-n)3-12(n-m)2
解:a(x-y)+b(y-x)
=a(x-y)
-b(x-y)
=
(x-y)(a-b)
解:6(m-n)3-12(n-m)2
=6(m-n)3
-12[-(m-n)]2
=
6(m-n)3-12(m-n)2
=6(m-n)2(m-n-2)
例题演示2
讲授新课
(1)3(a-b)2+6(b-a)
(2)x(x-y)2-y(y-x)2
(3)18(a-b)3-12b(b-a)2
(4)x(x+y)(x-y)
-x
(x+y)2
练习
解:原式=(2y+x)2[(2x-(x-2y)]
=(2y+x)2(x+2y)
=(2y+x)3
当x=2,y=3时
原式=(2×3+2)3
=83
=512
当x=2,y=3时,
注意解题格式
①将原式化简
②当。。。时,
代人最简式中计算。
提升练习
课后小结
谈谈本节课你有哪些收获?
(2)
5x(a-b)2+10y(b-a)2
)
3
(
2
3
)
(
12
)
(
6
m
n
n
m
-
-
-
)
(
)
(
)
1
(
x
y
b
y
x
a
-
-
-
7.把下列各式分解因式:
(4)
a(a+b)(a-b)-a(a+b)2
(5)
mn(m+n)-m(n+m)2
(6)
2(a-3)2-a+3
(7)
a(x-a)+b(a-x)-c(x-a)
讲授新课
1.判断下列各式是否正确?
(1)
(y-x)2
=
-(x-y)2
(2)
(3+2x)3
=
-(2x+3)3
(3)
a-2b
=
-(-2b+a)
(4)
-a+b
=
-(a+b)
(5)
(a-b)(x-2y)
=
(b-a)(2y-x)
否
否
否
否
对
随堂练习
2.把
a(x-3)+2b(x-3)
分解因式.
解:
a(x-3)+2b(x-3) =(x-3)(a+2b)
分析:
多项式可看成
a(x-3)
与
2b(x-3)
两项。
公因式为x-3
随堂练习
3.
把a(x-y)+b(y-x)分解因式.
解:
a(x-y)+b(y-x)
=a(x-y)-b(x-y) =(x-y)(a-b)
分析:多项式可看成a(x-y)与+b(y-x)两项。其中X-y与y-x互为相反数,可将+b(y-x)变为-b(x-y),
则a(x-y)与-b(x-y)
公因式为
x-y
随堂练习
4.
把6(m-n)3-12(n-m)2分解因式.
分析:其中(m-n)与(n-m)互为相反数.可将-12(n-m)
2变为-12(m-n)2,则6(m-n)3与-12(m-n)2
公因式为6(m-n)2
随堂练习
5.把6(x+y)(y-x)2-9(x-y)3分解因式.
解:
6(x+y)(y-x)2-
9(x-y)3
=
6(x+y)(x-y)2-
9(x-y)3
=
3(x-y)2[2(x+y)-3(x-y)]
=
3(x-y)2(2x+2y-3x+3y)
=
3(x-y)2(-x+5y)
=3(x-y)2(5y-x)
随堂练习
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
