第三章单元测试题（无答案）

第3章整章水平测试
一、填空题（每小题3分，共30分）
１、五边形的内角和为＿＿＿＿。
２、在 平行四边形ABCD 中，∠A＋∠C＝200°，则∠A＝＿＿＿＿。
3、如果矩形一条较短的边是 5，两条对角线的夹角是 60°，
　　则对角线长是＿＿＿＿。
4、菱形两条对角线的长分别是 12 和 16，则它的边长为＿＿＿＿。
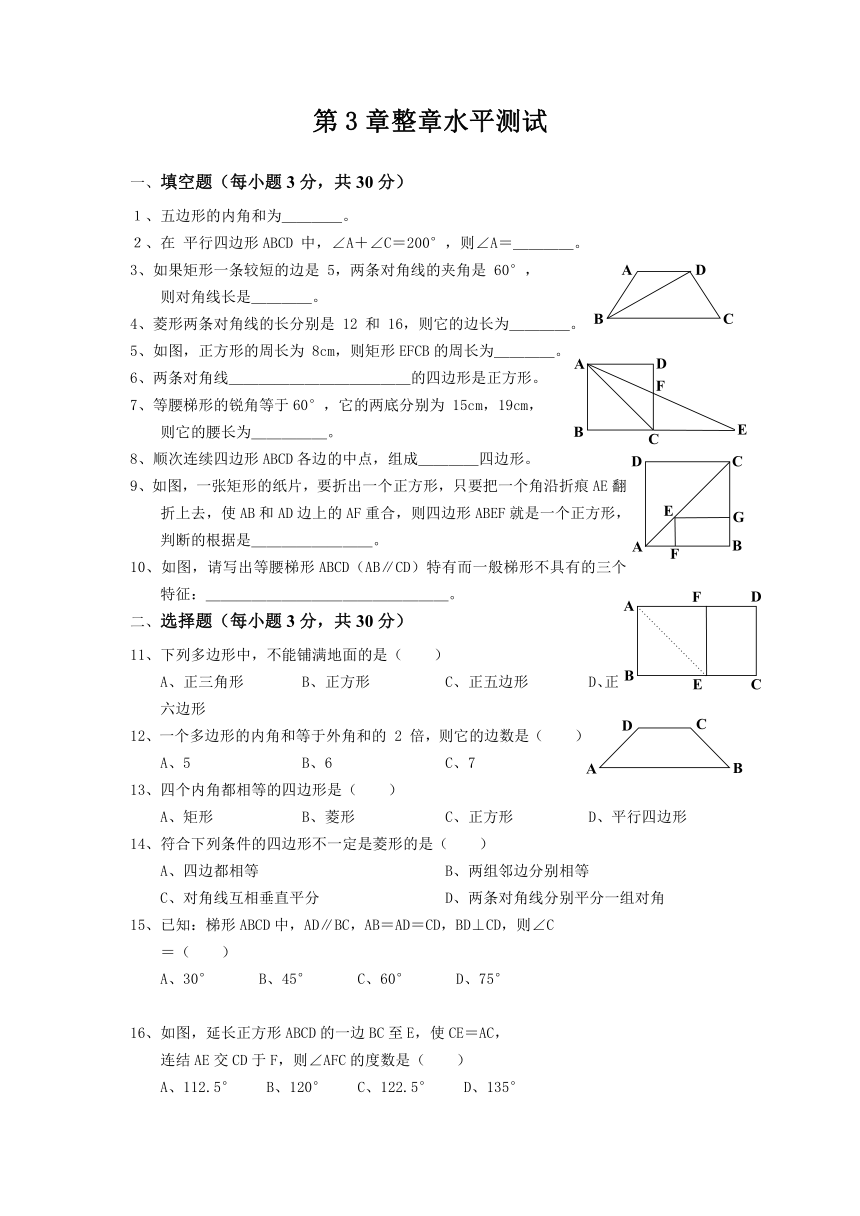
5、如图，正方形的周长为 8cm，则矩形EFCB的周长为＿＿＿＿。
6、两条对角线＿＿＿＿＿＿＿＿＿＿＿＿的四边形是正方形。
7、等腰梯形的锐角等于60°，它的两底分别为 15cm，19cm，
　　则它的腰长为＿＿＿＿＿。
8、顺次连续四边形ABCD各边的中点，组成＿＿＿＿四边形。
9、如图，一张矩形的纸片，要折出一个正方形，只要把一个角沿折痕AE翻折上去，使AB和AD边上的AF重合，则四边形ABEF就是一个正方形，判断的根据是＿＿＿＿＿＿＿＿。
10、如图，请写出等腰梯形ABCD（AB∥CD）特有而一般梯形不具有的三个特征：＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿。
二、选择题（每小题3分，共30分）
11、下列多边形中，不能铺满地面的是（　　）
　　A、正三角形 B、正方形 C、正五边形 D、正六边形
12、一个多边形的内角和等于外角和的 2 倍，则它的边数是（　　）
　　A、5 B、6 C、7 D、8
13、四个内角都相等的四边形是（　　）
　　A、矩形 B、菱形 C、正方形 D、平行四边形
14、符合下列条件的四边形不一定是菱形的是（　　）
　　A、四边都相等 B、两组邻边分别相等
　　C、对角线互相垂直平分 D、两条对角线分别平分一组对角
15、已知：梯形ABCD中，AD∥BC，AB＝AD＝CD，BD⊥CD，则∠C＝（　　）
　　A、30°　　　B、45°　　　C、60°　　　D、75°
16、如图，延长正方形ABCD的一边BC至E，使CE＝AC，连结AE交CD于F，则∠AFC的度数是（　　）
　　A、112.5°　　B、120°　　C、122.5°　　D、135°
17、矩形的边长为10 cm和15 cm，其中一内角平分线分长边为两部分，这两部分的长为（ ）
（A）6 cm和9 cm （B）5 cm和10 cm
（C）4 cm和11 cm （D）7 cm和8 cm
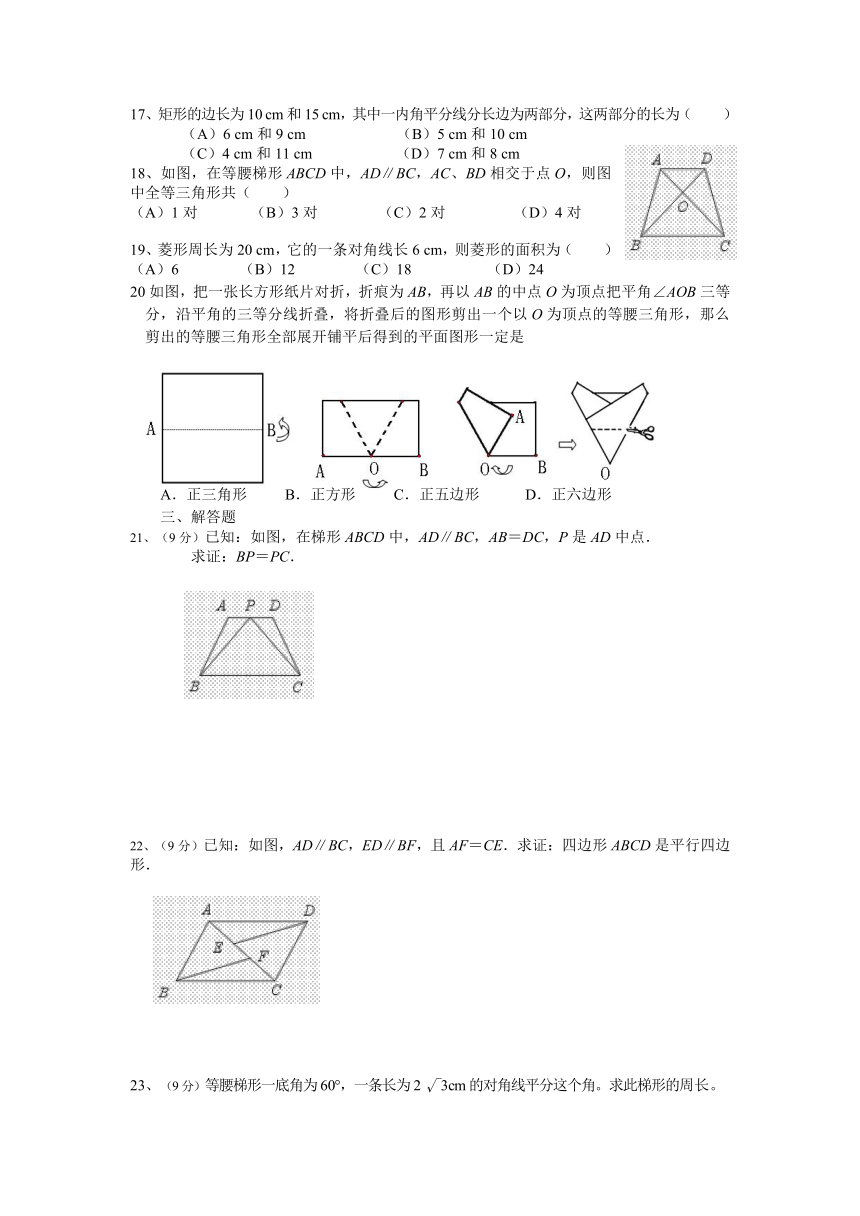
18、如图，在等腰梯形ABCD中，AD∥BC，AC、BD相交于点O，则图中全等三角形共（ ）
（A）1对 （B）3对 （C）2对 （D）4对
19、菱形周长为20 cm，它的一条对角线长6 cm，则菱形的面积为（ ）
（A）6 （B）12 （C）18 （D）24
20如图，把一张长方形纸片对折，折痕为AB，再以AB的中点O为顶点把平角∠AOB三等分，沿平角的三等分线折叠，将折叠后的图形剪出一个以O为顶点的等腰三角形，那么剪出的等腰三角形全部展开铺平后得到的平面图形一定是
A．正三角形 B．正方形 C．正五边形 D．正六边形
三、解答题
21、（9分）已知：如图，在梯形ABCD中，AD∥BC，AB＝DC，P是AD中点．
求证：BP＝PC．
22、（9分）已知：如图，AD∥BC，ED∥BF，且AF＝CE．求证：四边形ABCD是平行四边形．
23、（9分）等腰梯形一底角为60°，一条长为2 √3cm的对角线平分这个角。求此梯形的周长。
24、（9分）Rt△ABC中，∠C=90°。CD是AB边上的中线，过A作CD的平行线，过C作AB的平行线，两线交于E。
求证：四边形ADCE是菱形
25、（12分）等腰△ABC中，AB＝AC，Ｄ为BC上的一动点，DE∥AC ，DF∥AB，则DE＋DF是否随D点变化而变化？若不变化请证明。
26、（12分）已知：如图，在四边形ABCD中，E为AB上一点，△ADE和△BCE都是等边三角形，AB、BC、CD、DA的中点分别为P、Q、M、N，试判断四边形PQMN为怎样的四边形，并证明你的结论．
参考答案：
一、1、540°　
2、100°　　
3、10　　
4、10　　
5、4cm　　
6、互相垂直平分且相等　　
7、4cm　　
8、平行　　
9、邻边相等的矩形是正方形　　
10、AD＝BC，∠A＝∠B，AC＝BD
二、11、C
12、B
13、A
14、B
15、C
16、A
17、B
18、B
19、D
20、D
21、在梯形ABCD中，AD∥BC，
∵ AB＝DC，
∴ ∠A＝∠D．
∵ P是AD中点，
∴ AP＝DP．
在△ABP和△DCP中，
∴ △ABP≌△DCP．
∴ PB＝PC．
22、在△ADE和△CBF中，
∵ AD∥BC，
∴ ∠DAE＝∠BCF．
∵ ED∥BF，
∴ ∠DEF＝∠BFE．
∴ ∠DEA＝∠BFC．
∵ AF＝CE，
∴ AE＝CF．
∴ △ADE≌△CBF．
∴ AD＝BC．
又 AD∥BC，
∴ 四边形ABCD是平行四边形．
23、∵∠ABC=60°，BD平分∠ABC，
∴∠DBC=∠ABD=30°，
又∵∠C=∠ABC=60°
∴∠BDC=90°
在Rt△BDC中，BD=2 √3
∴CD= BC=2，BC=4
AB=CD=2
而AD∥BC，∠ADB=∠DBC=30°
∴AD=AB=2
∴AB+BC+CD+DA=2+4+2+2=10，答：此梯形的周长为10cm。
24、∵AECD，CEAD，
∴四边形ADCE是平行四边形，在Rt△ABC中，CD是斜边AB上的中线。
∴CD=1/2AB=AD
∴四边形ADCE是菱形
25、不变化。　　
∵DE∥AC，DF∥AB　
∴AEDF为平行四边形　　
∴DF＝AE　　
又∵AB＝AC
∴∠B＝∠C　　
∵ED∥AC　　
∴∠EDB＝∠C　
∴∠B＝∠EDB　　
∴ED＝BE
　　 ∴DE＋DF＝AE＋BE＝AB
26、四边形PQMN为菱形．证明如下：
如图，连结AC、BD．
∵ PQ为△ABC的中位线，
∴ PQ AC．
同理 MNAC．
∴ MNPQ，
∴ 四边形PQMN为平行四边形．
在△AEC和△DEB中，
AE＝DE，EC＝EB，∠AED＝60°＝∠CEB，
即 ∠AEC＝∠DEB．
∴ △AEC≌△DEB．
∴ AC＝BD．
∴ PQ＝AC＝BD＝PN．
∴ □PQMN为菱形．
A
D
B
C
A
E
F
B
G
C
D
A
B
C
D
A
B
E
C
D
F
A
D
F
E
C
B
A
B
D
C
E
F