冀教版数学七年级下册课件:第八章 整式的乘除 复习课 (共25张PPT)
文档属性
| 名称 | 冀教版数学七年级下册课件:第八章 整式的乘除 复习课 (共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 182.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-19 00:00:00 | ||
图片预览







文档简介
(共25张PPT)
第七章
整式的乘除
复习课
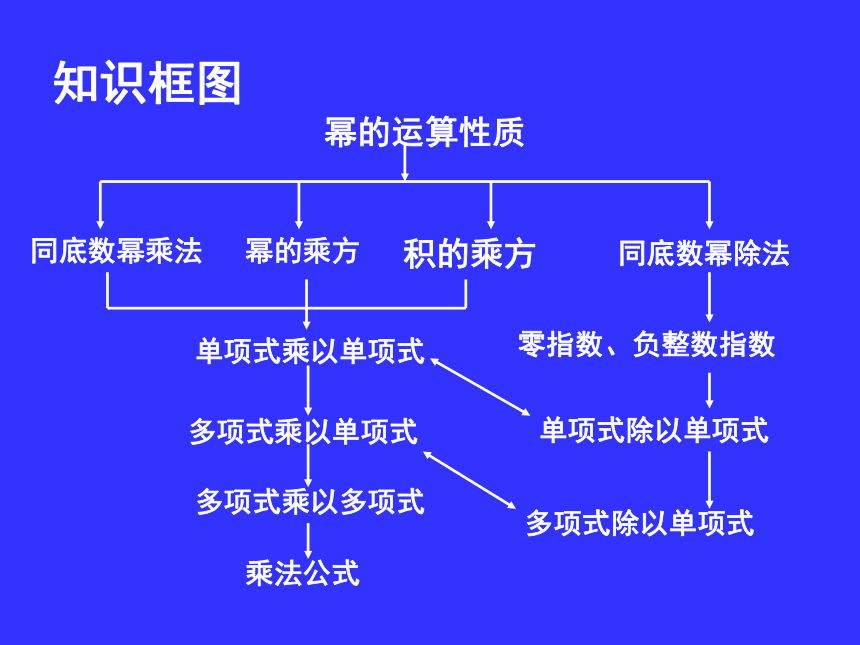
知识框图
幂的运算性质
同底数幂乘法
幂的乘方
积的乘方
同底数幂除法
单项式乘以单项式
零指数、负整数指数
多项式乘以单项式
单项式除以单项式
多项式乘以多项式
多项式除以单项式
乘法公式
同底数幂的乘法
aman=am+n
幂的乘方
(am)n=amn
积的乘方
(ab)n=anbn
底数不变指数相加
a既可以是数,也可以是“式”
底数不变指数相乘
与同底数幂的乘法不要混淆
将积中每个因式分别乘方,再相乘
积中每个因式都要乘方,不要丢项
一、幂的部分运算性质
知识点
法则简述
注意
例:比较大小:3555,4444,5333
解:3555=(35)111=243111
4444=(44)111=256111
5333=(53)111=125111
256﹥243﹥125
4444﹥3555﹥5333
例:如果
2×8n×16n=222,
求:n的值
解:
由2×8n×16n=222,得
2×(23)n×(24)n=222
21+3n+4n=222
2×23n×24n=222
所以:1+3n+4n=22
解得:n=3
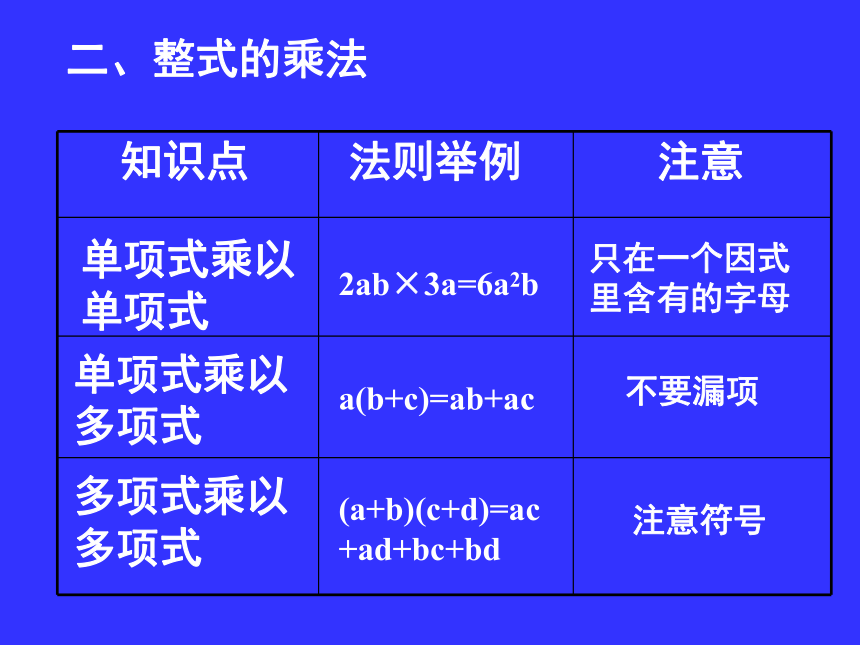
单项式乘以单项式
单项式乘以多项式
多项式乘以多项式
2ab×3a=6a2b
只在一个因式里含有的字母
a(b+c)=ab+ac
不要漏项
(a+b)(c+d)=ac+ad+bc+bd
注意符号
二、整式的乘法
知识点
法则举例
注意
计算(1)(ab2)3(ab2)4
解:(ab2)3(ab2)4
=(ab2)3+4
=x2y4(-x6y3)x8y8
(2)(xy2)2(-x2y)3(-x2y2)4
=(ab2)7
=a7b14
=-x16y15
计算(1)3x2y·(-5xy3z5)
解:
3x2y·(-5xy3z5)
=(-3×5)x2+1y1+3z5
=(0.5×0.2×10)a1+3+5b2+4c3
(2)0.5ab2·(-0.2a3b4)·(-10a5c3)
=-15x3y4z5
=a9b6c3
计算(1)(5a-3b)(4a+7b)
解:
(5a-3b)(4a+7b)
=5a×4a+5a×7b-3b×4a-3b×7b
=20a2+23ab-21b2
=20a2+35ab-12ab-21b2
三、乘法公式
平方差公式
完全平方公式
(a+b)(a-b)=a2-b2
字母a、b既可以是数,也可以是“式”
中间项的符号与等号左边相同
知识点
公式
注意
重点和难点:
重点:
乘法公式及其应用
难点:
对乘法公式结构特点的认识
需要熟悉的几个变形公式:
①a2+b2
=(a+b)2
–
2ab
②(a+b)2
=(a-b)2
+
4ab
③(a-b)2
=(a+b)2
-
4ab
④(a+b)2
-(a-b)2
=
4ab
=(a-b)2
+
2ab
例:已知
a+b=3,
a·b=2
求(1)a2+b2
(2)(a-b)2
解(1)a2+b2=(a+b)2-2ab
因为
a+b=3,
a·b=2
所以a2+b2=32-2×2=5
(2)(a-b)2
=(a+b)2-4ab
因为
a+b=3,
a·b=2
所以(a-b)2=32-4×2=1
例:已知(a+b)2=324,
(a-b)2=16
求(1)a2+b2
(2)ab
=170
(2)ab
=
=77
计算:
(1)(5x+6y-7z)(5x-6y+7z)
=[5x+(6y-7z)][5x-(6y-7z)]
=25x2-(6y-7z)2
=
25x2-36y2+84yz-49z2
(2)(x+2y-3z)(x-2y+3z)+(2y-3z)2
=[x+(2y-3z)][x-(2y-3z)]+
(2y-3z)2
=x2-(2y-3z)2+(2y-3z)2
=
x2
计算:(m-2n)2(m+2n)2(m2+4n2)2
=[(m-2n)(m+2n)]2(m2+4n2)2
=
(m2-4n2)2(m2+4n2)2
=[(m2-4n2)(m2+4n2)]2
=(m4-16n4)2
=m8-32m4n4+256n8
计算:(2x-3y-1)(-2x-3y+5)
=(2x-3y-3+2)(-2x-3y+3+2)
=[(2-3y)+(2x-3)][(2-3y)-(2x-3)]
=(2-3y)2-(2x-3)2
=4-12y+9y2-4x2+12x-9
=9y2-4x2-12y+12x-5
例:多项式4x2+1加上一个单项式后,使它能成为一个整式的完全平方,则求可能加上的单项式。
解:(1)将4x2+1看作是平方和,
(2)因为4x2本身就是完全平方,
则可以加上中间项:4x或-4x
所以加上-1即可。
综上所述:可以添加:
4x,
-4x,
4x4.
-4x2,
-1,
(3)因为1本身就是完全平方,
(4)将4x2
看作是中间项,
所以加上-4x2即可。
所以加上4x4即可。
例:设m2+m-1=0,
求m3+2m2+2003的值。
解:因为m2+m-1=0,
所以m2+m=1
故m3+m2=m
m3+2m2+2003
=m3+m2+m2+2003
=m2+m+2003
=1+2003
=2004
例:用适当方法化简算式:
(22+1)(24+1)(28+1)(216+1)
解:(22+1)(24+1)(28+1)(216+1)
=
(22+1)(24+1)(28+1)(216+1)
÷
(22-1)
[(22-1)
]
=[(24-1)(24+1)(28+1)(216+1)]÷3
=[(216-1)(216+1)]
÷3
=[(28-1)(28+1)(216+1)]÷3
同底数幂的除法
am÷an=am-n
单项式除以单项式
多项式除以多项式
底数不变指数相减
a0=1(a≠0)
6a2b÷2a=3ab
只在被除式里出现的字母
(ma+mb+mc)
÷m=a+b+c
1)符号
2)不要漏项
四、整式的除法
知识点
简述或举例
注意
计算:
(1)(a3)2÷a3
(2)(b2)3·(b3)2÷b4
(3)(a-2b)3·(a-2b)4÷(a-2b)5
=a3×2÷a3
=a6÷a3
=a6-3
=a3
=b2×3·b3×2÷b4
=b6+6-4
=b8
=(a-2b)3+4-5
=(a-2b)2
=a2-4ab+4b2
计算:
1.(-4x2+12x3y2-16x4y3)÷(-4x2)
2.[(2x-y)2+(2x+y)(2x-y)+4xy]÷4x
=-4x2÷(-4x2)+12x3y2÷(-4x2)-
16x4y3
÷(-4x2)
=1-3xy2+4x2y3
=(4x2-4xy+y2+4x2-y2+4xy)÷4x
=8x2÷4x
=2x
第七章
整式的乘除
复习课
知识框图
幂的运算性质
同底数幂乘法
幂的乘方
积的乘方
同底数幂除法
单项式乘以单项式
零指数、负整数指数
多项式乘以单项式
单项式除以单项式
多项式乘以多项式
多项式除以单项式
乘法公式
同底数幂的乘法
aman=am+n
幂的乘方
(am)n=amn
积的乘方
(ab)n=anbn
底数不变指数相加
a既可以是数,也可以是“式”
底数不变指数相乘
与同底数幂的乘法不要混淆
将积中每个因式分别乘方,再相乘
积中每个因式都要乘方,不要丢项
一、幂的部分运算性质
知识点
法则简述
注意
例:比较大小:3555,4444,5333
解:3555=(35)111=243111
4444=(44)111=256111
5333=(53)111=125111
256﹥243﹥125
4444﹥3555﹥5333
例:如果
2×8n×16n=222,
求:n的值
解:
由2×8n×16n=222,得
2×(23)n×(24)n=222
21+3n+4n=222
2×23n×24n=222
所以:1+3n+4n=22
解得:n=3
单项式乘以单项式
单项式乘以多项式
多项式乘以多项式
2ab×3a=6a2b
只在一个因式里含有的字母
a(b+c)=ab+ac
不要漏项
(a+b)(c+d)=ac+ad+bc+bd
注意符号
二、整式的乘法
知识点
法则举例
注意
计算(1)(ab2)3(ab2)4
解:(ab2)3(ab2)4
=(ab2)3+4
=x2y4(-x6y3)x8y8
(2)(xy2)2(-x2y)3(-x2y2)4
=(ab2)7
=a7b14
=-x16y15
计算(1)3x2y·(-5xy3z5)
解:
3x2y·(-5xy3z5)
=(-3×5)x2+1y1+3z5
=(0.5×0.2×10)a1+3+5b2+4c3
(2)0.5ab2·(-0.2a3b4)·(-10a5c3)
=-15x3y4z5
=a9b6c3
计算(1)(5a-3b)(4a+7b)
解:
(5a-3b)(4a+7b)
=5a×4a+5a×7b-3b×4a-3b×7b
=20a2+23ab-21b2
=20a2+35ab-12ab-21b2
三、乘法公式
平方差公式
完全平方公式
(a+b)(a-b)=a2-b2
字母a、b既可以是数,也可以是“式”
中间项的符号与等号左边相同
知识点
公式
注意
重点和难点:
重点:
乘法公式及其应用
难点:
对乘法公式结构特点的认识
需要熟悉的几个变形公式:
①a2+b2
=(a+b)2
–
2ab
②(a+b)2
=(a-b)2
+
4ab
③(a-b)2
=(a+b)2
-
4ab
④(a+b)2
-(a-b)2
=
4ab
=(a-b)2
+
2ab
例:已知
a+b=3,
a·b=2
求(1)a2+b2
(2)(a-b)2
解(1)a2+b2=(a+b)2-2ab
因为
a+b=3,
a·b=2
所以a2+b2=32-2×2=5
(2)(a-b)2
=(a+b)2-4ab
因为
a+b=3,
a·b=2
所以(a-b)2=32-4×2=1
例:已知(a+b)2=324,
(a-b)2=16
求(1)a2+b2
(2)ab
=170
(2)ab
=
=77
计算:
(1)(5x+6y-7z)(5x-6y+7z)
=[5x+(6y-7z)][5x-(6y-7z)]
=25x2-(6y-7z)2
=
25x2-36y2+84yz-49z2
(2)(x+2y-3z)(x-2y+3z)+(2y-3z)2
=[x+(2y-3z)][x-(2y-3z)]+
(2y-3z)2
=x2-(2y-3z)2+(2y-3z)2
=
x2
计算:(m-2n)2(m+2n)2(m2+4n2)2
=[(m-2n)(m+2n)]2(m2+4n2)2
=
(m2-4n2)2(m2+4n2)2
=[(m2-4n2)(m2+4n2)]2
=(m4-16n4)2
=m8-32m4n4+256n8
计算:(2x-3y-1)(-2x-3y+5)
=(2x-3y-3+2)(-2x-3y+3+2)
=[(2-3y)+(2x-3)][(2-3y)-(2x-3)]
=(2-3y)2-(2x-3)2
=4-12y+9y2-4x2+12x-9
=9y2-4x2-12y+12x-5
例:多项式4x2+1加上一个单项式后,使它能成为一个整式的完全平方,则求可能加上的单项式。
解:(1)将4x2+1看作是平方和,
(2)因为4x2本身就是完全平方,
则可以加上中间项:4x或-4x
所以加上-1即可。
综上所述:可以添加:
4x,
-4x,
4x4.
-4x2,
-1,
(3)因为1本身就是完全平方,
(4)将4x2
看作是中间项,
所以加上-4x2即可。
所以加上4x4即可。
例:设m2+m-1=0,
求m3+2m2+2003的值。
解:因为m2+m-1=0,
所以m2+m=1
故m3+m2=m
m3+2m2+2003
=m3+m2+m2+2003
=m2+m+2003
=1+2003
=2004
例:用适当方法化简算式:
(22+1)(24+1)(28+1)(216+1)
解:(22+1)(24+1)(28+1)(216+1)
=
(22+1)(24+1)(28+1)(216+1)
÷
(22-1)
[(22-1)
]
=[(24-1)(24+1)(28+1)(216+1)]÷3
=[(216-1)(216+1)]
÷3
=[(28-1)(28+1)(216+1)]÷3
同底数幂的除法
am÷an=am-n
单项式除以单项式
多项式除以多项式
底数不变指数相减
a0=1(a≠0)
6a2b÷2a=3ab
只在被除式里出现的字母
(ma+mb+mc)
÷m=a+b+c
1)符号
2)不要漏项
四、整式的除法
知识点
简述或举例
注意
计算:
(1)(a3)2÷a3
(2)(b2)3·(b3)2÷b4
(3)(a-2b)3·(a-2b)4÷(a-2b)5
=a3×2÷a3
=a6÷a3
=a6-3
=a3
=b2×3·b3×2÷b4
=b6+6-4
=b8
=(a-2b)3+4-5
=(a-2b)2
=a2-4ab+4b2
计算:
1.(-4x2+12x3y2-16x4y3)÷(-4x2)
2.[(2x-y)2+(2x+y)(2x-y)+4xy]÷4x
=-4x2÷(-4x2)+12x3y2÷(-4x2)-
16x4y3
÷(-4x2)
=1-3xy2+4x2y3
=(4x2-4xy+y2+4x2-y2+4xy)÷4x
=8x2÷4x
=2x
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
