沪科版九年级下册数学 第24章 圆 复习课件 (共30张PPT)
文档属性
| 名称 | 沪科版九年级下册数学 第24章 圆 复习课件 (共30张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-19 00:00:00 | ||
图片预览







文档简介
(共30张PPT)
欢迎046班的同学们!注意听课,积极思考呵!
第24章圆复习
1、圆的基本元素:
圆心、半径。
一、知识点:
2、圆的对称性:
圆的旋转对称性、圆是中心对称图形、圆是轴对称图形。
4、圆周角、圆心角、弦、弦心距的关系:
定理:在同圆或等圆中,相等的圆心角所对的弧相等,
所对的弦、所对弦心距的也相等。
推论:在同圆或等圆中,如果两个圆心角,两条弧,两条弦、两条弦心距中有一组量相等,那么它
们所对应的其余各组量都分别相等。
5过三点的圆:
(1)定理:不在同一直线上的三点确定一个圆。
(2)三角形的外接圆的圆心是三边的垂直平分线的交点。
3、垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧。
6、点与圆的位置关系:
①点在圆外;②点在圆上;
③点在圆内.
判断方法:
①交点个数
②点与圆心的
距离d和半径r的大小关系.
7、直线与圆的位置关系:
①相离,②相切,
③相交.
判断方法:
①交点个数
②圆心与直线的距离d和半径r的大小关系.
8、两圆的位置关系:
①外离
②相切
③相交
④内切
⑤内含
判断方法:
①交点个数
②圆心距d与半径r1、r2的大小关系.
9、圆的切线:
(1)与圆有唯一一个交点的直线是圆的切线。
(2)切线的判定定理:经过半径的外端点且垂直于这条半径的直线是圆的切线。
(3)切线性质定理:________________________。
10、切线长定理:________________________。
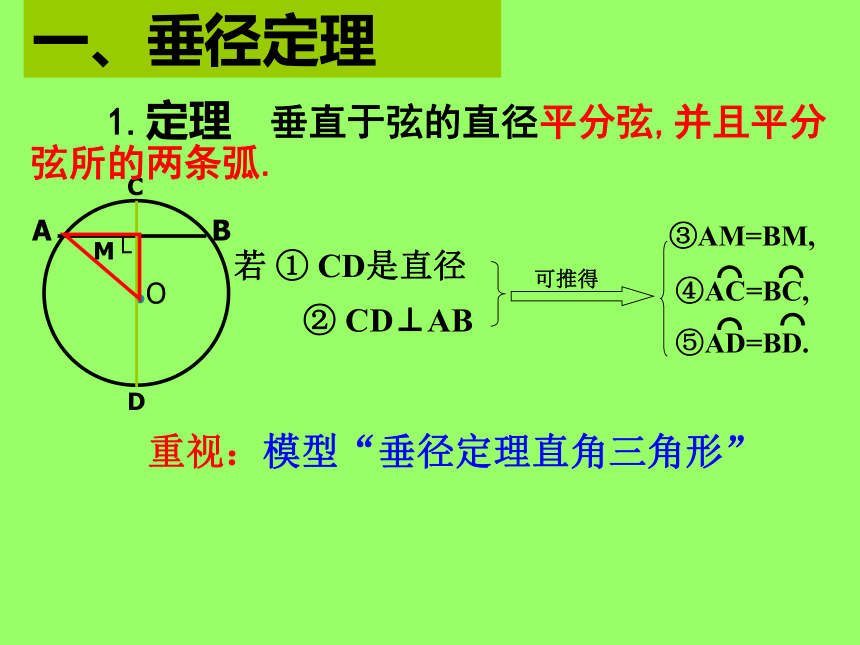
一、垂径定理
③AM=BM,
重视:模型“垂径定理直角三角形”
若
①
CD是直径
②
CD⊥AB
1.定理
垂直于弦的直径平分弦,并且平分弦所的两条弧.
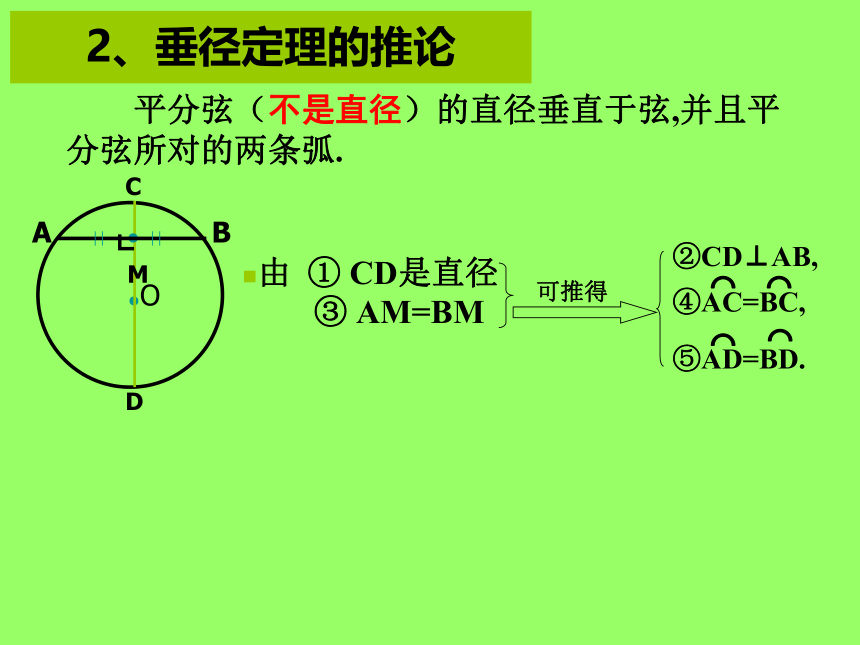
2、垂径定理的推论
平分弦(不是直径)的直径垂直于弦,并且平
分弦所对的两条弧.
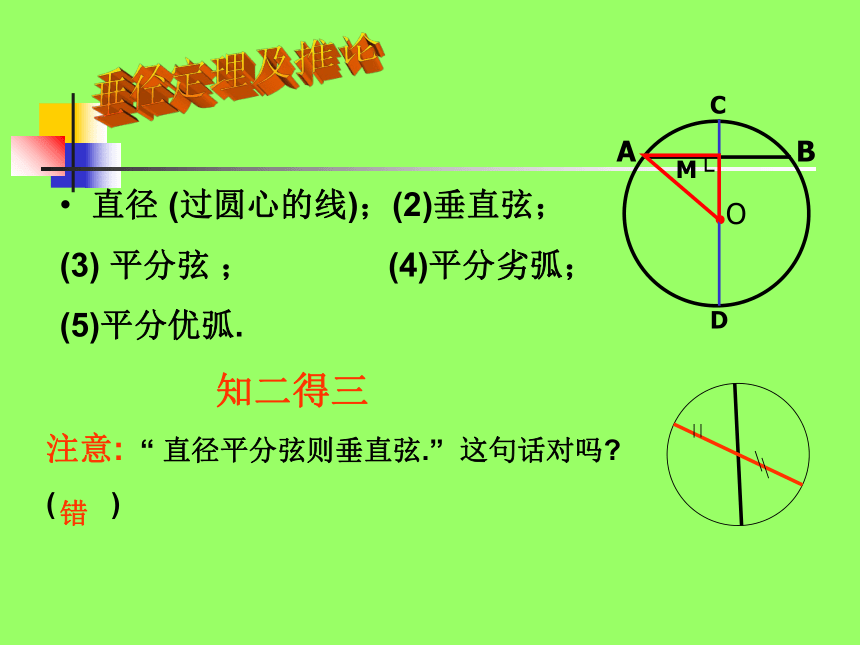
直径
(过圆心的线);(2)垂直弦;
(3)
平分弦
; (4)平分劣弧;
(5)平分优弧.
知二得三
注意:
“
直径平分弦则垂直弦.”
这句话对吗?
(
)
错
例⊙O的半径为10cm,弦AB∥CD,
AB=16,CD=12,则AB、CD间的
距离是___
.
2cm
或14cm
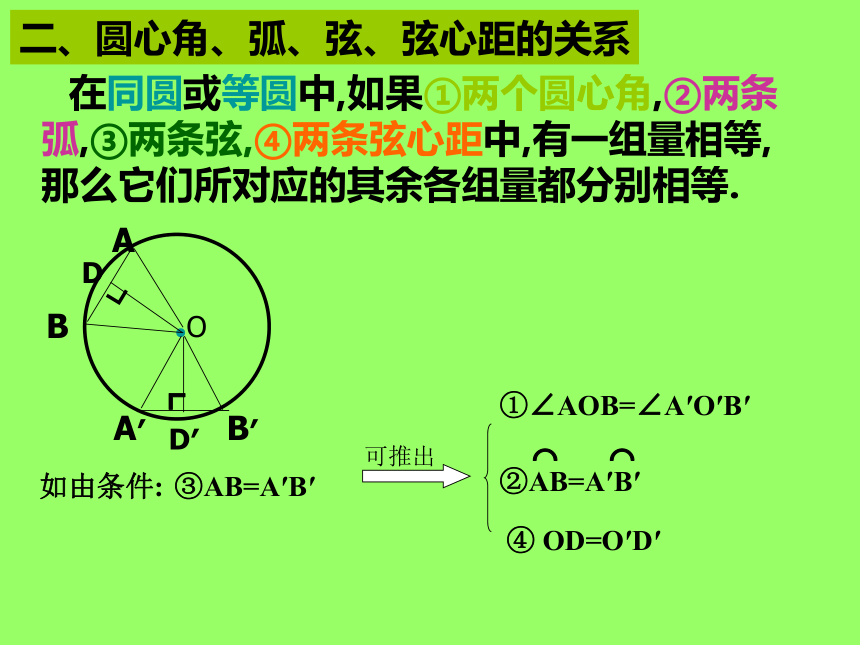
在同圆或等圆中,如果①两个圆心角,②两条弧,③两条弦,④两条弦心距中,有一组量相等,那么它们所对应的其余各组量都分别相等.
如由条件:
③AB=A′B′
④
OD=O′D′
①∠AOB=∠A′O′B′
二、圆心角、弧、弦、弦心距的关系
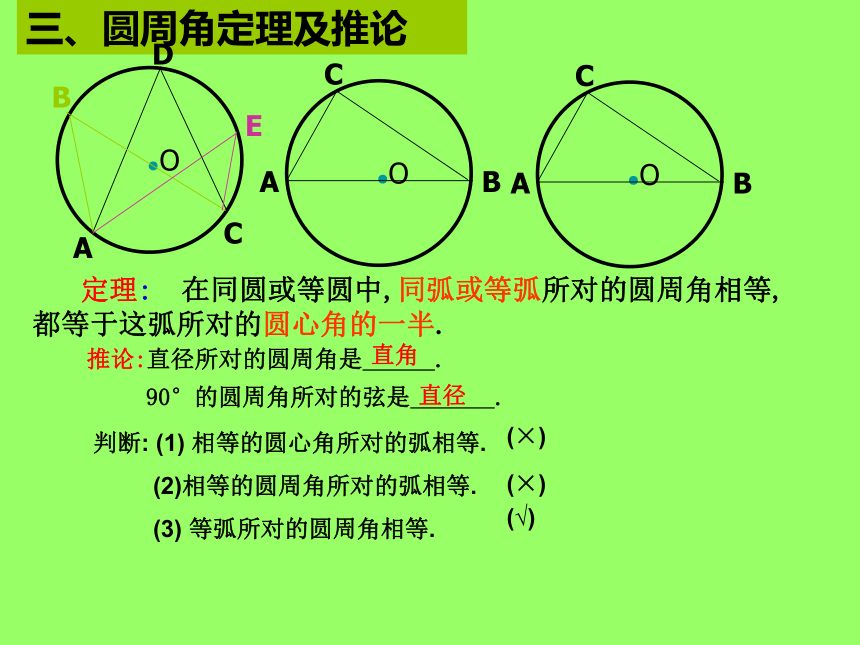
三、圆周角定理及推论
90°的圆周角所对的弦是
.
定理:
在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这弧所对的圆心角的一半.
推论:直径所对的圆周角是
.
直角
直径
判断:
(1)
相等的圆心角所对的弧相等.
(2)相等的圆周角所对的弧相等.
(3)
等弧所对的圆周角相等.
(×)
(×)
(√)
四、点和圆的位置关系
1、⊙O的半径为R,圆心到点A的距离为d,且R、d分别是方程x2-6x+8=0的两根,则点A与⊙O的位置关系是(
)
A.点A在⊙O内部
B.点A在⊙O上
C.点A在⊙O外部
D.点A不在⊙O上
2、M是⊙O内一点,已知过点M的⊙O最长的弦为10
cm,最短的弦长为8
cm,则OM=_____
cm.
3、圆内接四边形ABCD中,∠A∶∠B∶∠C∶∠D可以是(
)
A、1∶2∶3∶4
B、1∶3∶2∶4
C、4∶2∶3∶1
D、4∶2∶1∶3
6
1、直线和圆相交
d
r;
d
r;
2、直线和圆相切
3、直线和圆相离
d
r.
五.直线与圆的位置关系
<
=
>
切线的判定定理
定理
经过半径的外端,并且垂直于这条半径的直线是圆的切线.
C
D
●O
A
如图
∵OA是⊙O的半径,
且CD⊥OA,
∴
CD是⊙O的切线.
(1)定义
(2)圆心到直线的距离d=圆的半径r
(3)切线的判定定理:经过半径的外端,并且垂直于这条半径的直线是圆的切线.
切线的判定定理的两种应用
1、如果已知直线与圆有交点,往往要作出过这一点的半径,再证明直线垂直于这条半径即可;
2、如果不明确直线与圆的交点,往往要作出圆心到直线的垂线段,再证明这条垂线段等于半径即可.
切线的性质定理
圆的切线垂直于过切点的半径.
∵CD切⊙O于A,
OA是⊙O的半径
C
D
●O
A
∴CD⊥OA.
切线的性质定理出可理解为
如果一条直线满足以下三个性质中的任意两个,那么
第三个也成立。①经过切点、②垂直于切线、③经过圆心。
如 ①
②
③
①
③
②
②
③
①
1、两个同心圆的半径分别为3
cm和4
cm,大圆的弦BC与小圆相切,则BC=_____
cm;
2、如图2,在以O为圆心的两个同心圆
中,大圆的弦AB是小圆的切线,P为切点,
设AB=12,则两圆构成圆环面积为_____;
3、下列四个命题中正确的是(
).
①与圆有公共点的直线是该圆的切线
;
②垂直于圆的半径的直线是该圆的切线
;
③到圆心的距离等于半径的直线是该圆的切线
;④过圆直径的端点,垂直于此直径的直线是该圆的切线.
A.①②
B.②③
C.③④
D.①④
2
C
一、判断。
1、三角形的外心到三角形各边的距离相等;
(
)
2、直角三角形的外心是斜边的中点.
(
)
二、填空:
1、直角三角形的两条直角边分别是5cm和12cm,则它的外接圆
半径 ,内切圆半径 ;
2、等边三角形外接圆半径与内切圆半径之比 .
三、选择题:
下列命题正确的是(
)
A、三角形外心到三边距离相等
B、三角形的内心不一定在三角形的内部
C、等边三角形的内心、外心重合
D、三角形一定有一个外切圆
×
√
6.5cm
2cm
2:1
C
四、一个三角形,它的周长为30cm,它的内切圆半径为2cm,则这个三角形的面积为______.
30cm
A
B
C
O
七.三角形的外接圆和内切圆:
A
B
C
I
三角形内切圆的圆心叫三角形的内心。
三角形外接圆的圆心叫三角形的外心
三角形三边垂直平分线的交点
三角形三内角角平分线的交点
到三角形各边的距离相等
到三角形各顶点的距离相等
实质
性质
三角形的外心
三角形的内心
锐角三角形的外心位于三角形内,
直角三角形的外心位于直角三角形斜边中点,
钝角三角形的外心位于三角形外.
三角形的外心是否一定在三角形的内部?
从圆外一点向圆所引的两条切线长相等;并且这一点和圆心的连线平分两条切线的夹角.
切线长定理及其推论:
直角三角形的内切圆半径与三边关系.
三角形的内切圆半径与圆面积.
∵PA,PB切⊙O于A,B
∴PA=PB
∠1=∠2
1.如图:圆O中弦AB等于半径R,则这条弦所对的圆心角是___,圆周角是______.
60度
30或150度
2:已知ABC三点在圆O上,连接ABCO,如果∠
AOC=140
°,求∠
B的度数.
3.平面上一点P到圆O上一点的距离最长为6cm,最短为2cm,则圆O的半径为_______.
D
解:在优弧AC上定一点D,连结AD、
CD.
∵
∠
AOC=140
°
∴
∠
D=70
°
∴
∠
B=180
°
-70
°
=110
°
2或4cm
4.怎样要将一个如图所示的破镜重圆?
A
B
C
P
5、
如图,AB是⊙O的任意一条弦,OC⊥AB,垂足为P,若
CP=7cm,AB=28cm
,你能帮老师求出这面镜子的半径吗?
O
7
14
综合应用垂径定理和勾股定理可求得半径
6.如图:AB是圆O的直径,BD是圆O的弦,延长BD到C,AC=AB,BD与CD的大小有什么关系?
为什么?
补充:
若∠B=70
°,则∠DOE=___.
E
40
°
7、如图,AB是圆O的直径,圆O过AC的中点D,DE⊥BC于E.
证明:DE是圆O的切线.
谢谢同们的合作
拜 拜
欢迎046班的同学们!注意听课,积极思考呵!
第24章圆复习
1、圆的基本元素:
圆心、半径。
一、知识点:
2、圆的对称性:
圆的旋转对称性、圆是中心对称图形、圆是轴对称图形。
4、圆周角、圆心角、弦、弦心距的关系:
定理:在同圆或等圆中,相等的圆心角所对的弧相等,
所对的弦、所对弦心距的也相等。
推论:在同圆或等圆中,如果两个圆心角,两条弧,两条弦、两条弦心距中有一组量相等,那么它
们所对应的其余各组量都分别相等。
5过三点的圆:
(1)定理:不在同一直线上的三点确定一个圆。
(2)三角形的外接圆的圆心是三边的垂直平分线的交点。
3、垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧。
6、点与圆的位置关系:
①点在圆外;②点在圆上;
③点在圆内.
判断方法:
①交点个数
②点与圆心的
距离d和半径r的大小关系.
7、直线与圆的位置关系:
①相离,②相切,
③相交.
判断方法:
①交点个数
②圆心与直线的距离d和半径r的大小关系.
8、两圆的位置关系:
①外离
②相切
③相交
④内切
⑤内含
判断方法:
①交点个数
②圆心距d与半径r1、r2的大小关系.
9、圆的切线:
(1)与圆有唯一一个交点的直线是圆的切线。
(2)切线的判定定理:经过半径的外端点且垂直于这条半径的直线是圆的切线。
(3)切线性质定理:________________________。
10、切线长定理:________________________。
一、垂径定理
③AM=BM,
重视:模型“垂径定理直角三角形”
若
①
CD是直径
②
CD⊥AB
1.定理
垂直于弦的直径平分弦,并且平分弦所的两条弧.
2、垂径定理的推论
平分弦(不是直径)的直径垂直于弦,并且平
分弦所对的两条弧.
直径
(过圆心的线);(2)垂直弦;
(3)
平分弦
; (4)平分劣弧;
(5)平分优弧.
知二得三
注意:
“
直径平分弦则垂直弦.”
这句话对吗?
(
)
错
例⊙O的半径为10cm,弦AB∥CD,
AB=16,CD=12,则AB、CD间的
距离是___
.
2cm
或14cm
在同圆或等圆中,如果①两个圆心角,②两条弧,③两条弦,④两条弦心距中,有一组量相等,那么它们所对应的其余各组量都分别相等.
如由条件:
③AB=A′B′
④
OD=O′D′
①∠AOB=∠A′O′B′
二、圆心角、弧、弦、弦心距的关系
三、圆周角定理及推论
90°的圆周角所对的弦是
.
定理:
在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这弧所对的圆心角的一半.
推论:直径所对的圆周角是
.
直角
直径
判断:
(1)
相等的圆心角所对的弧相等.
(2)相等的圆周角所对的弧相等.
(3)
等弧所对的圆周角相等.
(×)
(×)
(√)
四、点和圆的位置关系
1、⊙O的半径为R,圆心到点A的距离为d,且R、d分别是方程x2-6x+8=0的两根,则点A与⊙O的位置关系是(
)
A.点A在⊙O内部
B.点A在⊙O上
C.点A在⊙O外部
D.点A不在⊙O上
2、M是⊙O内一点,已知过点M的⊙O最长的弦为10
cm,最短的弦长为8
cm,则OM=_____
cm.
3、圆内接四边形ABCD中,∠A∶∠B∶∠C∶∠D可以是(
)
A、1∶2∶3∶4
B、1∶3∶2∶4
C、4∶2∶3∶1
D、4∶2∶1∶3
6
1、直线和圆相交
d
r;
d
r;
2、直线和圆相切
3、直线和圆相离
d
r.
五.直线与圆的位置关系
<
=
>
切线的判定定理
定理
经过半径的外端,并且垂直于这条半径的直线是圆的切线.
C
D
●O
A
如图
∵OA是⊙O的半径,
且CD⊥OA,
∴
CD是⊙O的切线.
(1)定义
(2)圆心到直线的距离d=圆的半径r
(3)切线的判定定理:经过半径的外端,并且垂直于这条半径的直线是圆的切线.
切线的判定定理的两种应用
1、如果已知直线与圆有交点,往往要作出过这一点的半径,再证明直线垂直于这条半径即可;
2、如果不明确直线与圆的交点,往往要作出圆心到直线的垂线段,再证明这条垂线段等于半径即可.
切线的性质定理
圆的切线垂直于过切点的半径.
∵CD切⊙O于A,
OA是⊙O的半径
C
D
●O
A
∴CD⊥OA.
切线的性质定理出可理解为
如果一条直线满足以下三个性质中的任意两个,那么
第三个也成立。①经过切点、②垂直于切线、③经过圆心。
如 ①
②
③
①
③
②
②
③
①
1、两个同心圆的半径分别为3
cm和4
cm,大圆的弦BC与小圆相切,则BC=_____
cm;
2、如图2,在以O为圆心的两个同心圆
中,大圆的弦AB是小圆的切线,P为切点,
设AB=12,则两圆构成圆环面积为_____;
3、下列四个命题中正确的是(
).
①与圆有公共点的直线是该圆的切线
;
②垂直于圆的半径的直线是该圆的切线
;
③到圆心的距离等于半径的直线是该圆的切线
;④过圆直径的端点,垂直于此直径的直线是该圆的切线.
A.①②
B.②③
C.③④
D.①④
2
C
一、判断。
1、三角形的外心到三角形各边的距离相等;
(
)
2、直角三角形的外心是斜边的中点.
(
)
二、填空:
1、直角三角形的两条直角边分别是5cm和12cm,则它的外接圆
半径 ,内切圆半径 ;
2、等边三角形外接圆半径与内切圆半径之比 .
三、选择题:
下列命题正确的是(
)
A、三角形外心到三边距离相等
B、三角形的内心不一定在三角形的内部
C、等边三角形的内心、外心重合
D、三角形一定有一个外切圆
×
√
6.5cm
2cm
2:1
C
四、一个三角形,它的周长为30cm,它的内切圆半径为2cm,则这个三角形的面积为______.
30cm
A
B
C
O
七.三角形的外接圆和内切圆:
A
B
C
I
三角形内切圆的圆心叫三角形的内心。
三角形外接圆的圆心叫三角形的外心
三角形三边垂直平分线的交点
三角形三内角角平分线的交点
到三角形各边的距离相等
到三角形各顶点的距离相等
实质
性质
三角形的外心
三角形的内心
锐角三角形的外心位于三角形内,
直角三角形的外心位于直角三角形斜边中点,
钝角三角形的外心位于三角形外.
三角形的外心是否一定在三角形的内部?
从圆外一点向圆所引的两条切线长相等;并且这一点和圆心的连线平分两条切线的夹角.
切线长定理及其推论:
直角三角形的内切圆半径与三边关系.
三角形的内切圆半径与圆面积.
∵PA,PB切⊙O于A,B
∴PA=PB
∠1=∠2
1.如图:圆O中弦AB等于半径R,则这条弦所对的圆心角是___,圆周角是______.
60度
30或150度
2:已知ABC三点在圆O上,连接ABCO,如果∠
AOC=140
°,求∠
B的度数.
3.平面上一点P到圆O上一点的距离最长为6cm,最短为2cm,则圆O的半径为_______.
D
解:在优弧AC上定一点D,连结AD、
CD.
∵
∠
AOC=140
°
∴
∠
D=70
°
∴
∠
B=180
°
-70
°
=110
°
2或4cm
4.怎样要将一个如图所示的破镜重圆?
A
B
C
P
5、
如图,AB是⊙O的任意一条弦,OC⊥AB,垂足为P,若
CP=7cm,AB=28cm
,你能帮老师求出这面镜子的半径吗?
O
7
14
综合应用垂径定理和勾股定理可求得半径
6.如图:AB是圆O的直径,BD是圆O的弦,延长BD到C,AC=AB,BD与CD的大小有什么关系?
为什么?
补充:
若∠B=70
°,则∠DOE=___.
E
40
°
7、如图,AB是圆O的直径,圆O过AC的中点D,DE⊥BC于E.
证明:DE是圆O的切线.
谢谢同们的合作
拜 拜
