人教版(五四制)六年级数学下册第九章几何图形初步 单元测试含答案
文档属性
| 名称 | 人教版(五四制)六年级数学下册第九章几何图形初步 单元测试含答案 |
|
|
| 格式 | zip | ||
| 文件大小 | 100.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-19 00:00:00 | ||
图片预览




文档简介
六年级数学(下)
第九章《几何图形初步》
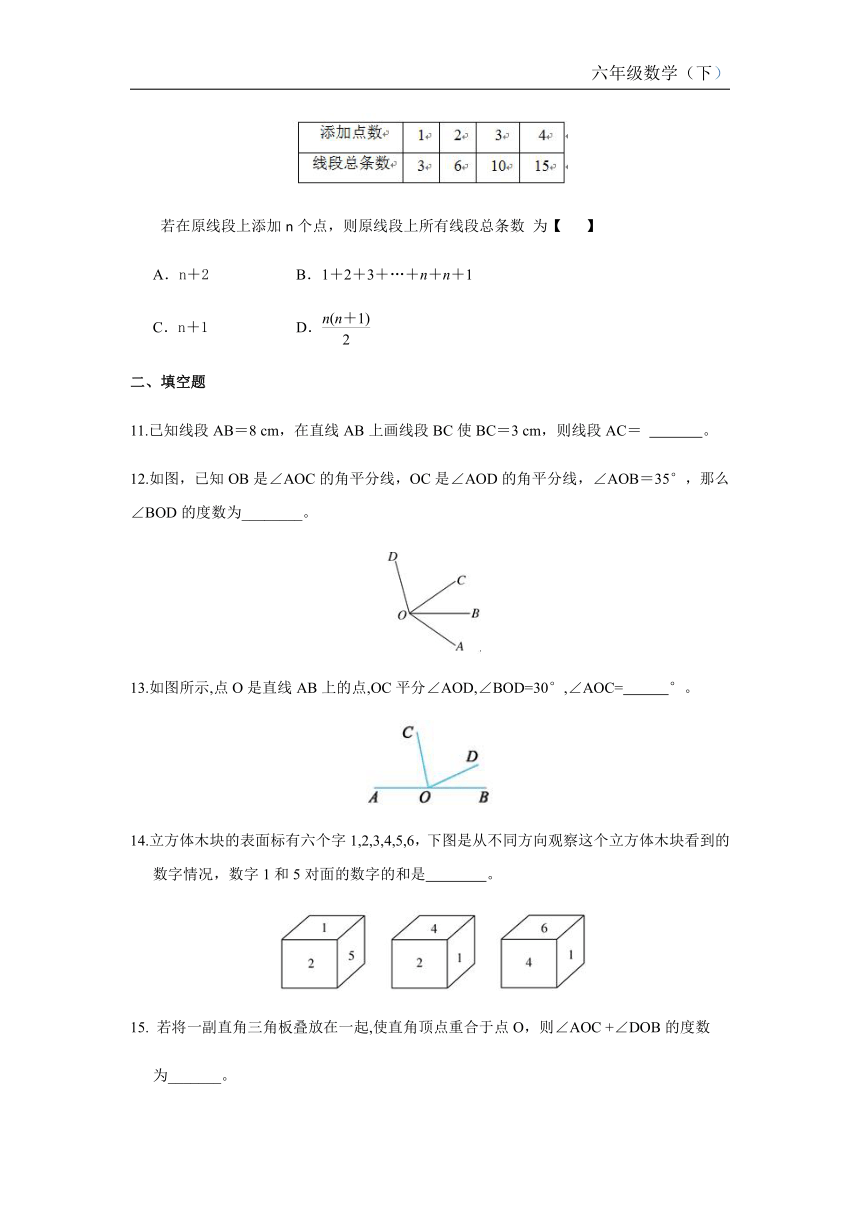
一、选择题
1.
把弯曲的河道改直,能够缩短船舶航行的路程,这样做的道理是【
】
A.垂线段最短
B.两点确定一条直线
C.两点之间,直线最短
D.两点之间,线段最短
2.
下列现象中,可用基本事实“两点之间,线段最短”来解释的现象是【
】
A.用两个钉子就可以把木条固定在墙上
B.利用圆规可以比较两条线段的大小关系
C.把弯曲的公路改直,就能缩短路程
D.植树时,只要定出两棵树的位置,就能确定同一行树所在的直线
3.
一个几何体的展开图如图所示,则这个几何体是【
】
A.三棱柱
B.三棱锥
C.四棱柱
D.四棱锥
4.
如图是一个正方体纸巾盒,它的平面展开图是【
】
5.
如图所示,点C是线段AB的中点,点D是线段BC的中点,则下列结论中错误的是【
】
A.AB=4CD
B.AD=AB-BD
C.AB=BC+2CD
D.AD=2CD
6.
用一副三角板不能画出【
】
A.75°角
B.135°角
C.160°角
D.105°角
7.
如果线段AB=10
cm,MA+MB=15
cm,那么下面说法中正确的是【
】
A.M点在线段AB上
B.M点在直线AB上
C.M点在直线AB外
D.M点可能在直线AB上,也可能在直线AB外
8.
下列四个生活、生产现象:①用两个钉子就可以把木条固定在墙上;②植树时,只要定出两棵树的位置,就能确定同一行树所在的直线;③从A地到B地架设电线,总是尽可能沿着线段AB架设;④把弯曲的公路改直,就能缩短路程。其中可用公理“两点之间,线段最短”来解释的现象有【
】
A.①②
B.①③
C.②④
D.③④
9.
将一副直角三角尺如图放置,若∠AOD=20°,则∠BOC的大小为【
】
A.140°
B.160°
C.170°
D.150°
10.
已知在线段上依次添加1个点,2个点,3个点,……,原线段上所成线段的总条数如下表:
若在原线段上添加n个点,则原线段上所有线段总条数
为【
】
A.n+2
B.1+2+3+…+n+n+1
C.n+1
D.
二、填空题
11.已知线段AB=8
cm,在直线AB上画线段BC使BC=3
cm,则线段AC=
。
12.如图,已知OB是∠AOC的角平分线,OC是∠AOD的角平分线,∠AOB=35°,那么∠BOD的度数为________。
13.如图所示,点O是直线AB上的点,OC平分∠AOD,∠BOD=30°,∠AOC=
°。
14.立方体木块的表面标有六个字1,2,3,4,5,6,下图是从不同方向观察这个立方体木块看到的数字情况,数字1和5对面的数字的和是
。
15.
若将一副直角三角板叠放在一起,使直角顶点重合于点O,则∠AOC
+∠DOB的度数
为_______。
三、解答题
16.(8分)已知∠α=76°,∠β=41°31′,
求:
(1)∠β的余角;
(2)∠α的2倍与∠β的的差。
17.(9分)一个角的补角比它的余角的3倍小20°,求这个角的度数。
18.(9分)如图所示,点C,D为线段AB的三等分点,点E为线段AC的中点.若ED=9,求线段AB的长度。
19.(9分)如图,点O是射线OC与直线AB的交点.
(1)若∠1=120°,求∠2的度数;
(2)若已知∠1的一半比∠2小30°,求∠1和∠2的度数。
20.(9分)(1)如图1,已知点D是线段AC的中点,点B在线段DC上,且AB=4BC,若BD=6
cm,求AB的长;
(2)如图2,∠AOB=∠COD=90°,OC平分∠AOB,∠BOD=3∠DOE,试求∠COE的度数。
21.(10分)如图,已知点O在线段AB上,点C,D分别是AO,BO的中点.
(1)AO=________CO;BO=________DO;
(2)若CO=3cm,DO=2cm,求线段AB的长度;
(3)若线段AB=10,小明很轻松地求得CD=5.他在反思过程中突发奇想:若点O在线段AB的延长线上,原有的结论“CD=5”是否仍然成立呢?请帮小明画出图形分析,并说明理由。
22.(10分)如图,O是直线AB上一点,OD平分∠AOC.
(1)若∠AOC=60°,请求出∠AOD和∠BOC的度数.
(2)若∠AOD和∠DOE互余,且∠AOD=∠AOE,请求出∠AOD和∠COE的度数。
23.(11分)把一副三角板的直角顶点O重叠在一起,
(1)如图1,当OB平分∠COD时,则∠AOD和∠BOC的和是多少度?
(2)如图2,当OB不平分∠COD时,则∠AOD和∠BOC的和是多少度?
(3)当∠BOC的余角的4倍等于∠AOD时,则∠BOC是多少度?
参考答案
1
2
3
4
5
6
7
8
9
10
D
C
B
B
D
C
D
D
B
B
11
12
13
14
15
5cm或11cm
105°
75
7
180°
16.【答案】(1)48°29′;(2)131°14′30″。
【解析】解:(1)∠β的余角=90°-∠β=90°-41°31′=48°29′;
(2)∵∠α=76°,∠β=41°31′,
∴2∠α-∠β=2×76°-×41°31′=152°-20°45′30″=131°14′30″。
17.【答案】35°.
【解析】解:设这个角的度数为x°,由题意,得
180-x=3(90-x)-20,
解得x=35.
答:这个角的度数为35°。
18.【答案】18
【解析】解:设AB=x,因为点C,D为线段AB的三等分点,所以AC=CD=DB=
x;因为点E为线段AC的中点,所以AE=EC=
x;因为ED=9,所以x+x=9,解得x=18,所以AB的长度为18。
19.【答案】(1)∠2=60°;(2)∠1=100°,∠2
=80°
【解析】略.
20.【答案】(1)16cm;(2)75°。
【解析】解:(1)因为AB=4BC,AB+BC=AC,
所以AC=5BC.
因为点D是线段AC的中点,
所以AD=DC=AC=BC.
因为BD=DC-BC=6
cm,
所以BC-BC=6
cm.
所以BC=4
cm.
所以AB=4BC=16
cm.
(2)因为∠AOB=90°,OC平分∠AOB,
所以∠BOC=∠AOB=45°.
因为∠BOD=∠COD-∠BOC=90°-45°=45°,∠BOD=3∠DOE,
所以∠DOE=15°.
所以∠COE=∠COD-∠DOE=90°-15°=75°
21.【答案】(1)2、2;(2)10cm;(3)5cm。
【解析】解:(1)2、2;
(2)∵点C,D分别是AO,BO的中点,CO=3cm,DO=2cm,
∴AO=2CO=6cm,BO=2DO=4cm,∴AB=AO+BO=6+4=10(cm)。
(3)仍然成立,如图:
理由如下:∵点C,D分别是AO,BO的中点,∴CO=AO,DO=BO,∴CD=CO-DO=AO-BO=(AO-BO)=AB=×10=5(cm)。
22.【答案】(1)∠AOD=30°,∠BOC=120°;(2)∠AOD=∠COE
=30°
【解析】略。
23.【答案】(1)180°;(2)180°;(3)60°。
【解析】解:(1)当OB平分∠COD时,有∠BOC=∠BOD=45°,
于是∠AOC=90°-45°=45°,
∴∠AOD+∠BOC=∠AOC+∠COD+∠BOC=45°+90°+45°=180°.
(2)当OB不平分∠COD时,
有∠AOB=∠AOC+∠BOC=90°,∠COD=∠BOD+∠BOC=90°,
于是∠AOD+∠BOC=∠AOC+∠BOC+∠BOD+∠BOC
=∠AOB+∠COD=90°+90°=180°.
(3)由(2)得∠AOD+∠BOC=180°,
有∠AOD=180°-∠BOC,
180°-∠BOC=4(90°-∠BOC),
∴∠BOC=60°
第九章《几何图形初步》
一、选择题
1.
把弯曲的河道改直,能够缩短船舶航行的路程,这样做的道理是【
】
A.垂线段最短
B.两点确定一条直线
C.两点之间,直线最短
D.两点之间,线段最短
2.
下列现象中,可用基本事实“两点之间,线段最短”来解释的现象是【
】
A.用两个钉子就可以把木条固定在墙上
B.利用圆规可以比较两条线段的大小关系
C.把弯曲的公路改直,就能缩短路程
D.植树时,只要定出两棵树的位置,就能确定同一行树所在的直线
3.
一个几何体的展开图如图所示,则这个几何体是【
】
A.三棱柱
B.三棱锥
C.四棱柱
D.四棱锥
4.
如图是一个正方体纸巾盒,它的平面展开图是【
】
5.
如图所示,点C是线段AB的中点,点D是线段BC的中点,则下列结论中错误的是【
】
A.AB=4CD
B.AD=AB-BD
C.AB=BC+2CD
D.AD=2CD
6.
用一副三角板不能画出【
】
A.75°角
B.135°角
C.160°角
D.105°角
7.
如果线段AB=10
cm,MA+MB=15
cm,那么下面说法中正确的是【
】
A.M点在线段AB上
B.M点在直线AB上
C.M点在直线AB外
D.M点可能在直线AB上,也可能在直线AB外
8.
下列四个生活、生产现象:①用两个钉子就可以把木条固定在墙上;②植树时,只要定出两棵树的位置,就能确定同一行树所在的直线;③从A地到B地架设电线,总是尽可能沿着线段AB架设;④把弯曲的公路改直,就能缩短路程。其中可用公理“两点之间,线段最短”来解释的现象有【
】
A.①②
B.①③
C.②④
D.③④
9.
将一副直角三角尺如图放置,若∠AOD=20°,则∠BOC的大小为【
】
A.140°
B.160°
C.170°
D.150°
10.
已知在线段上依次添加1个点,2个点,3个点,……,原线段上所成线段的总条数如下表:
若在原线段上添加n个点,则原线段上所有线段总条数
为【
】
A.n+2
B.1+2+3+…+n+n+1
C.n+1
D.
二、填空题
11.已知线段AB=8
cm,在直线AB上画线段BC使BC=3
cm,则线段AC=
。
12.如图,已知OB是∠AOC的角平分线,OC是∠AOD的角平分线,∠AOB=35°,那么∠BOD的度数为________。
13.如图所示,点O是直线AB上的点,OC平分∠AOD,∠BOD=30°,∠AOC=
°。
14.立方体木块的表面标有六个字1,2,3,4,5,6,下图是从不同方向观察这个立方体木块看到的数字情况,数字1和5对面的数字的和是
。
15.
若将一副直角三角板叠放在一起,使直角顶点重合于点O,则∠AOC
+∠DOB的度数
为_______。
三、解答题
16.(8分)已知∠α=76°,∠β=41°31′,
求:
(1)∠β的余角;
(2)∠α的2倍与∠β的的差。
17.(9分)一个角的补角比它的余角的3倍小20°,求这个角的度数。
18.(9分)如图所示,点C,D为线段AB的三等分点,点E为线段AC的中点.若ED=9,求线段AB的长度。
19.(9分)如图,点O是射线OC与直线AB的交点.
(1)若∠1=120°,求∠2的度数;
(2)若已知∠1的一半比∠2小30°,求∠1和∠2的度数。
20.(9分)(1)如图1,已知点D是线段AC的中点,点B在线段DC上,且AB=4BC,若BD=6
cm,求AB的长;
(2)如图2,∠AOB=∠COD=90°,OC平分∠AOB,∠BOD=3∠DOE,试求∠COE的度数。
21.(10分)如图,已知点O在线段AB上,点C,D分别是AO,BO的中点.
(1)AO=________CO;BO=________DO;
(2)若CO=3cm,DO=2cm,求线段AB的长度;
(3)若线段AB=10,小明很轻松地求得CD=5.他在反思过程中突发奇想:若点O在线段AB的延长线上,原有的结论“CD=5”是否仍然成立呢?请帮小明画出图形分析,并说明理由。
22.(10分)如图,O是直线AB上一点,OD平分∠AOC.
(1)若∠AOC=60°,请求出∠AOD和∠BOC的度数.
(2)若∠AOD和∠DOE互余,且∠AOD=∠AOE,请求出∠AOD和∠COE的度数。
23.(11分)把一副三角板的直角顶点O重叠在一起,
(1)如图1,当OB平分∠COD时,则∠AOD和∠BOC的和是多少度?
(2)如图2,当OB不平分∠COD时,则∠AOD和∠BOC的和是多少度?
(3)当∠BOC的余角的4倍等于∠AOD时,则∠BOC是多少度?
参考答案
1
2
3
4
5
6
7
8
9
10
D
C
B
B
D
C
D
D
B
B
11
12
13
14
15
5cm或11cm
105°
75
7
180°
16.【答案】(1)48°29′;(2)131°14′30″。
【解析】解:(1)∠β的余角=90°-∠β=90°-41°31′=48°29′;
(2)∵∠α=76°,∠β=41°31′,
∴2∠α-∠β=2×76°-×41°31′=152°-20°45′30″=131°14′30″。
17.【答案】35°.
【解析】解:设这个角的度数为x°,由题意,得
180-x=3(90-x)-20,
解得x=35.
答:这个角的度数为35°。
18.【答案】18
【解析】解:设AB=x,因为点C,D为线段AB的三等分点,所以AC=CD=DB=
x;因为点E为线段AC的中点,所以AE=EC=
x;因为ED=9,所以x+x=9,解得x=18,所以AB的长度为18。
19.【答案】(1)∠2=60°;(2)∠1=100°,∠2
=80°
【解析】略.
20.【答案】(1)16cm;(2)75°。
【解析】解:(1)因为AB=4BC,AB+BC=AC,
所以AC=5BC.
因为点D是线段AC的中点,
所以AD=DC=AC=BC.
因为BD=DC-BC=6
cm,
所以BC-BC=6
cm.
所以BC=4
cm.
所以AB=4BC=16
cm.
(2)因为∠AOB=90°,OC平分∠AOB,
所以∠BOC=∠AOB=45°.
因为∠BOD=∠COD-∠BOC=90°-45°=45°,∠BOD=3∠DOE,
所以∠DOE=15°.
所以∠COE=∠COD-∠DOE=90°-15°=75°
21.【答案】(1)2、2;(2)10cm;(3)5cm。
【解析】解:(1)2、2;
(2)∵点C,D分别是AO,BO的中点,CO=3cm,DO=2cm,
∴AO=2CO=6cm,BO=2DO=4cm,∴AB=AO+BO=6+4=10(cm)。
(3)仍然成立,如图:
理由如下:∵点C,D分别是AO,BO的中点,∴CO=AO,DO=BO,∴CD=CO-DO=AO-BO=(AO-BO)=AB=×10=5(cm)。
22.【答案】(1)∠AOD=30°,∠BOC=120°;(2)∠AOD=∠COE
=30°
【解析】略。
23.【答案】(1)180°;(2)180°;(3)60°。
【解析】解:(1)当OB平分∠COD时,有∠BOC=∠BOD=45°,
于是∠AOC=90°-45°=45°,
∴∠AOD+∠BOC=∠AOC+∠COD+∠BOC=45°+90°+45°=180°.
(2)当OB不平分∠COD时,
有∠AOB=∠AOC+∠BOC=90°,∠COD=∠BOD+∠BOC=90°,
于是∠AOD+∠BOC=∠AOC+∠BOC+∠BOD+∠BOC
=∠AOB+∠COD=90°+90°=180°.
(3)由(2)得∠AOD+∠BOC=180°,
有∠AOD=180°-∠BOC,
180°-∠BOC=4(90°-∠BOC),
∴∠BOC=60°
