人教版初二数学下册19.2.3一次函数与方程、不等式课件(79张)
文档属性
| 名称 | 人教版初二数学下册19.2.3一次函数与方程、不等式课件(79张) |

|
|
| 格式 | zip | ||
| 文件大小 | 8.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-19 00:00:00 | ||
图片预览






文档简介
(共79张PPT)
初二年级
数学
一次函数与方程、不等式
学习目标
1.理解一次函数与一元一次方程、
一元一次不等式、和二元一次方程(组)之间的关系.会用函数观点解释方程(组)和不等式及其解(解集)的意义.
2.经历用函数图象表示方程(组)、不等式的过程,进一步体会“以形表示数,以数解释形”的数形结合思想.
1、一次函数与一元一次方程:
问题1.
下面3个方程有什么共同点和不同点?你能从函数的角度
对解这3个方程进行解释吗?
(1)
;(2)
;(3)
.
1、一次函数与一元一次方程:
问题1.
下面3个方程有什么共同点和不同点?你能从函数的角度
对解这3个方程进行解释吗?
(1)
;(2)
;(3)
.
相同之处:这3个方程等号的左边都是
;
不同之处:等号右边分别为
3、0、-1.
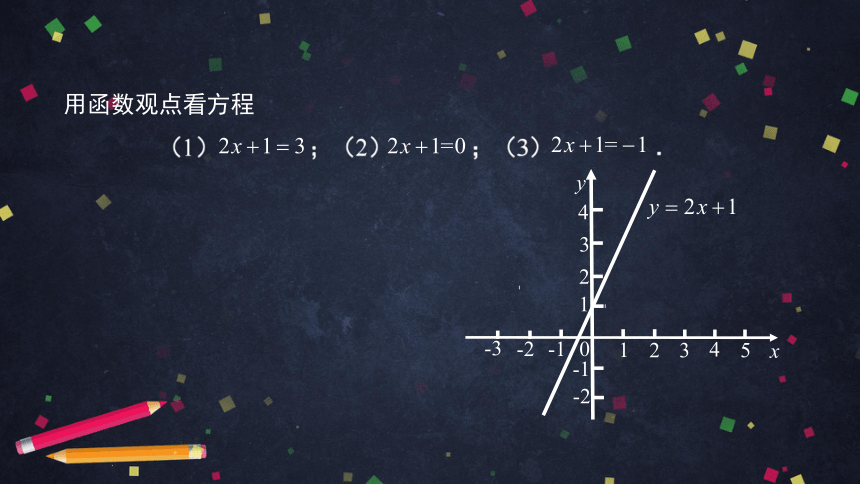
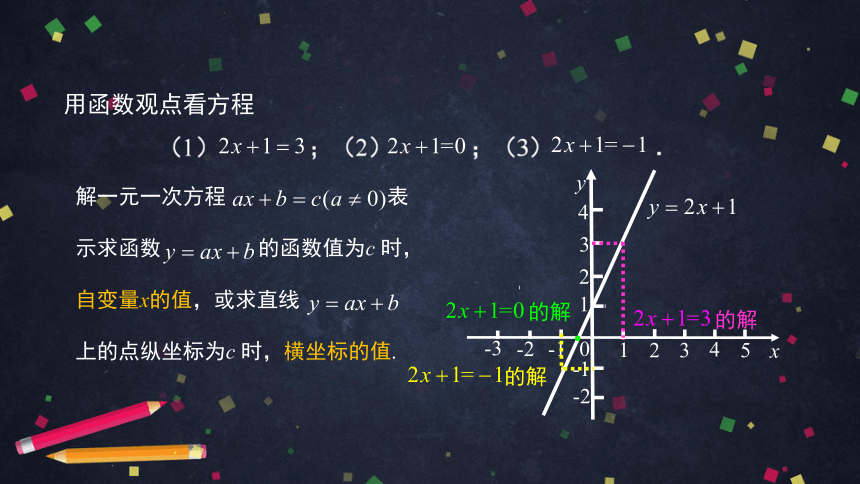
用函数观点看方程
(1)
;(2)
;(3)
.
用函数观点看方程
(1)
;(2)
;(3)
.
1
-1
-2
0
2
3
4
1
2
3
4
5
-1
-2
-3
x
y
用函数观点看方程
(1)
;(2)
;(3)
.
1
-1
-2
0
2
3
4
1
2
3
4
5
-1
-2
-3
x
y
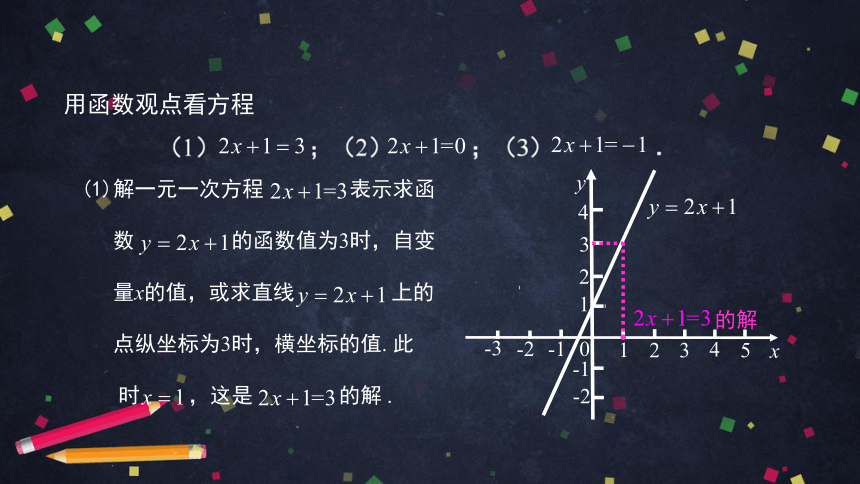
的解
解一元一次方程
表示求函
数
的函数值为3时,自变
量x的值,或求直线
上的
点纵坐标为3时,横坐标的值.
此
时
,这是
的解
.
用函数观点看方程
(1)
;(2)
;(3)
.
1
-1
-2
0
2
3
4
1
2
3
4
5
-1
-2
-3
x
y
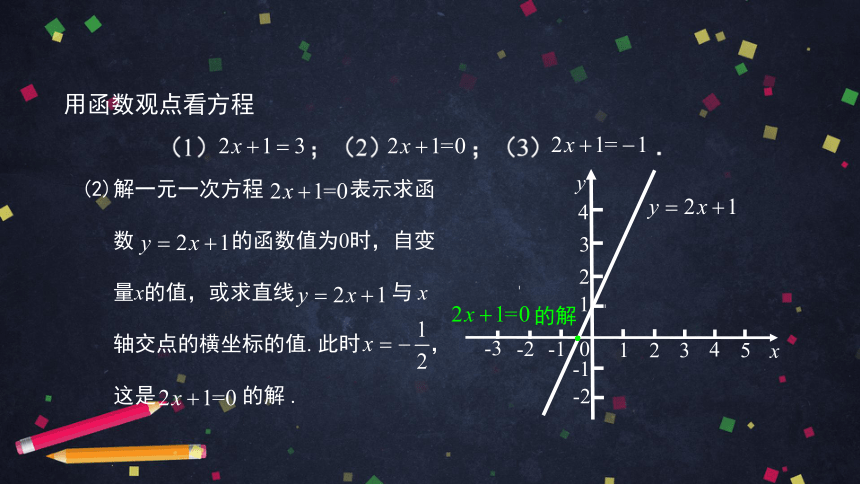
的解
(2)解一元一次方程
表示求函
数
的函数值为0时,自变
量x的值,或求直线
与
x
轴交点的横坐标的值.
此时
,
这是
的解
.
用函数观点看方程
(1)
;(2)
;(3)
.
1
-1
-2
0
2
3
4
1
2
3
4
5
-1
-2
-3
x
y
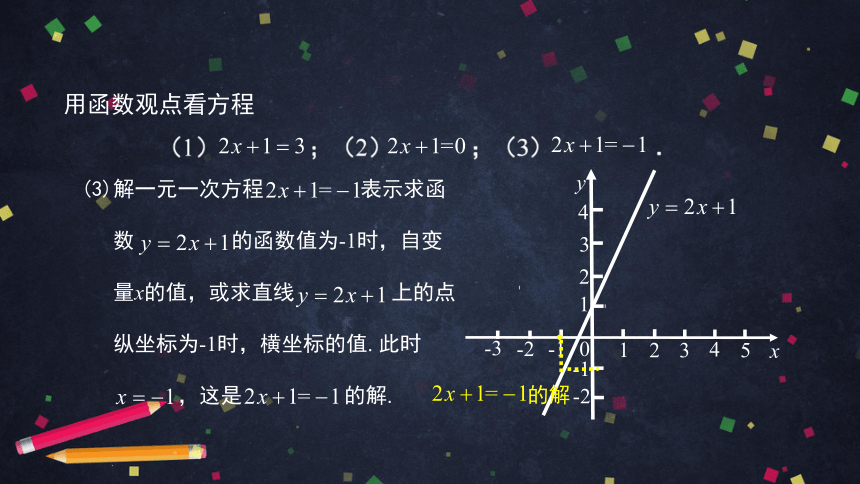
的解
(3)解一元一次方程
表示求函
数
的函数值为-1时,自变
量x的值,或求直线
上的点
纵坐标为-1时,横坐标的值.
此时
,这是
的解.
用函数观点看方程
(1)
;(2)
;(3)
.
1
-1
-2
0
2
3
4
1
2
3
4
5
-1
-2
-3
x
y
的解
的解
的解
解一元一次方程
表
示求函数
的函数值为c
时,
自变量x的值,或求直线
上的点纵坐标为c
时,横坐标的值.
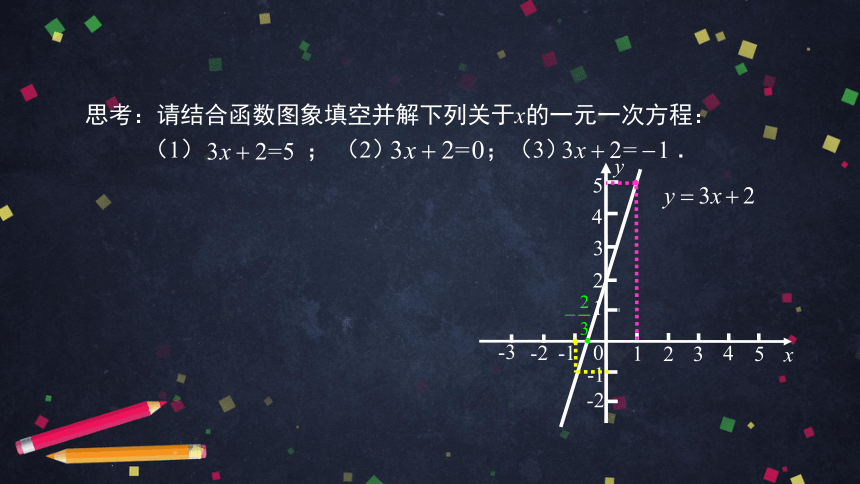
思考:请结合函数图象填空并解下列关于x的一元一次方程:
(1)
;
(2)
;(3)
.
1
-1
-2
0
2
3
4
1
2
3
4
5
-1
-2
-3
x
y
5
思考:请结合函数图象填空并解下列关于x的一元一次方程:
(1)
;
(2)
;(3)
.
1
-1
-2
0
2
3
4
1
2
3
4
5
-1
-2
-3
x
y
5
(1)解方程
表示求函数__________
的函数值为_5_时,自变量x的取值,也即
求直线__________上的点纵坐标为_5_时,
横坐标x的取值.
因此方程
的
解为_______.
1
-1
-2
0
2
3
4
1
2
3
4
5
-1
-2
-3
x
y
5
(2)解方程
表示求函数__________
的函数值为_0_时,自变量x的取值,也即
求直线__________与x轴交点的_横坐标
的
值.
因此方程
的解为_______.
思考:请结合函数图象填空并解下列关于x的一元一次方程:
(1)
;
(2)
;(3)
.
1
-1
-2
0
2
3
4
1
2
3
4
5
-1
-2
-3
x
y
5
(3)解方程
表示求函数__________
的函数值为_-1_时,自变量x的取值,也即
求直线__________上的点纵坐标为_-1_时,
横坐标x的取值.
因此方程
的
解为_______.
思考:请结合函数图象填空并解下列关于x的一元一次方程:
(1)
;
(2)
;(3)
.
思考:请结合函数图象填空并解下列关于x的一元一次方程:
(1)
;
(2)
;(3)
.
1
-1
-2
0
2
3
4
1
2
3
4
5
-1
-2
-3
x
y
5
解一元一次方程
表
示求函数
的函数值为c时,
自变量x的值,或求直线
上的点纵坐标为c
时,横坐标的值.
归纳小结:
归纳小结:
从函数的概念的角度来理解一元一次方程
的解,它是函数
在随自变量x变化过程中的一个状态,也就是函数值为c时的这个状态.
归纳小结:
从函数的概念的角度来理解一元一次方程
的解,它是函数
在随自变量x变化过程中的一个状态,也就是函数值为c时的这个状态.
求一元一次方程
的解.
求一次函数
的值为c时,对应的自变量x
的值.
从函数值看
1
-1
-2
0
2
3
4
1
2
3
4
5
-1
-2
-3
x
y
的解
的解
的解
求一元一次方程
的解.
求直线
上的点的纵坐标为c时横坐标x的值;当
时,即求直线与x轴交点的横坐标的值.
从函数图象看
2、一次函数与一元一次不等式:
问题2.
下面3个不等式有什么共同点和不同点?你能从函数的角
度对解这3个不等式进行解释吗?
(1)
;(2)
;(3)
.
2、一次函数与一元一次不等式:
相同之处:这3个不等式的不等号左边都是
不同之处:不等号及不等号右边不同.
问题2.
下面3个不等式有什么共同点和不同点?你能从函数的角
度对解这3个不等式进行解释吗?
(1)
;(2)
;(3)
.
用函数观点看下列不等式:
,
,
,
.
上述四个不等式的解集共用一个临界值
时,自变量的取值.
用函数观点看下列不等式:
,
,
,
.
1
-1
-2
0
2
3
4
1
2
3
4
-1
-2
-3
x
y
5
用函数观点看下列不等式:
,
,
,
.
1
-1
-2
0
2
3
4
1
2
3
4
-1
-2
-3
x
y
5
解
表示求函数
的函数值
大于5时,或求直线
在直线
的
上方时,自变量x的取值范围.
用函数观点看下列不等式:
,
,
,
.
1
-1
-2
0
2
3
4
1
2
3
4
-1
-2
-3
x
y
5
解
表示求函数
的函数值
大于5时,或求直线
在直线
的
上方时,自变量x的取值范围.所以
的解集为
.
用函数观点看下列不等式:
,
,
,
.
1
-1
-2
0
2
3
4
1
2
3
4
-1
-2
-3
x
y
5
解
表示求函数
的函数值
小于5时,或求直线
在直线
的
下方时,自变量x的取值范围.所以
的解集为
.
用函数观点看下列不等式:
,
,
,
.
1
-1
-2
0
2
3
4
1
2
3
4
-1
-2
-3
x
y
5
解
表示求函数
的函数值
大于等于5时,或求直线
在直线
的上方含交点时,自变量x的取值范
围.所以
的解集为
.
用函数观点看下列不等式:
,
,
,
.
1
-1
-2
0
2
3
4
1
2
3
4
-1
-2
-3
x
y
5
解
表示求函数
的函数值
小于等于5时,或求直线
在直线
的下方含交点时,自变量x的取值范
围.所以
的解集为
.
用函数观点看不等式
(2)
;
(3)
.
1
-1
-2
0
2
3
4
1
2
3
4
-1
-2
-3
x
y
5
用函数观点看不等式
(2)
;
(3)
.
1
-1
-2
0
2
3
4
1
2
3
4
-1
-2
-3
x
y
5
(2)解
表示求函数
的函数
值小于0时,或求直线
在x轴下
方时,自变量x的取值范围.所以
的解集为
.
用函数观点看不等式
(2)
;
(3)
.
1
-1
-2
0
2
3
4
1
2
3
4
-1
-2
-3
x
y
5
(3)解
表示求函数
的函
数值大于-1时,或求直线
在
上方时,自变量x的取值范围.所
以
的解集为
.
解一元一次不等式
就是求当函数
的函数值值大于c(小于c)时,或求直线
在直线
上方(或下方)时,自变量x
的取值范围.
用函数观点看解不等式:
(1)
;(2)
;(3)
.
归纳小结:
归纳小结:
从函数的概念的角度来理解一元一次不等式
(
)(
)
的解集,它是函数
在随自变量x变化过程中的一段状态,也就是函数值大于c(或大于等于c
)时的这段状态.
归纳小结:
从函数的概念的角度来理解一元一次不等式
(
)(
)
的解集,它是函数
在随自变量x变化过程中的一段状态,也就是函数值大于c(或大于等于c
)时的这段状态.
求一次函数
的值大于c(大于等于c)时,自变量x
的取值范围.
从函数值看
求
(
)
(
)
的解集.
确定直线
在
上方
(上方含交点)时,自变量x
的取值范围.
当
时,
为x轴.
从函数图象看
求
(
)
(
)
的解集.
确定直线
在
上方
(上方含交点)时,自变量x
的取值范围.
当
时,
为x轴.
从函数图象看
求
(
)
(
)
的解集.
请思考总结如何从函数值和函数图象两个角度来解释求一元一次不等式
和
吗?
3、一次函数与二元一次方程:
问题3.
1号探测气球从海拔5m处出发,以1m/min的速度上升.与此同时,2号探测气球从海拔15m处出发,以0.5m/min的速度上升.
两个气球都上升了1h.
(1)
请用解析式分别表示两个气球所在位置的海
拔y(单位:m)与气球上升时间x(单位:min)
的函数关系.
3、一次函数与二元一次方程:
问题3.
1号探测气球从海拔5m处出发,以1m/min的速度上升.与此同时,2号探测气球从海拔15m处出发,以0.5m/min的速度上升.
两个气球都上升了1h.
(1)
请用解析式分别表示两个气球所在位置的海
拔y(单位:m)与气球上升时间x(单位:min)
的函数关系.
气球1
海拔高度:
;
3、一次函数与二元一次方程:
问题3.
1号探测气球从海拔5m处出发,以1m/min的速度上升.与此同时,2号探测气球从海拔15m处出发,以0.5m/min的速度上升.
两个气球都上升了1h.
(1)
请用解析式分别表示两个气球所在位置的海
拔y(单位:m)与气球上升时间x(单位:min)
的函数关系.
气球1
海拔高度:
;
气球2
海拔高度:
.
(2)
在某时刻两个气球能否位于同一高度?如果能,这时气球上升了多
长时间?位于什么高度?
(2)
在某时刻两个气球能否位于同一高度?如果能,这时气球上升了多
长时间?位于什么高度?
解得:
从二元一次方程组(数)的角度:
当上升20min时,两个气球都位于海拔25m高度.
从一次函数图象(形)的角度:
从一次函数图象(形)的角度:
y
x
10
20
15
5
30
25
20
15
10
5
O
/min
/m
从一次函数图象(形)的角度:
y
x
10
20
15
5
30
25
20
15
10
5
O
/min
/m
从一次函数图象(形)的角度:
这表示当20min时,气球1和气球2都位于海拔25m的高度.
y
x
10
20
15
5
30
25
20
15
10
5
O
/min
/m
归纳小结:
归纳小结:
任何一个含有未知数x
和y
的二元一次方程都可以改写为
(k,b是常数,
)的形式,所以每一个这样的方程都对应着一个一次函数,于是也对应一条直线.
直线上每一个点的坐标
都是这个二元一次方程的解.
归纳小结:
任何一个含有未知数x
和y
的二元一次方程都可以改写为
(k,b是常数,
)的形式,所以每一个这样的方程都对应着一个一次函数,于是也对应一条直线.
直线上每一个点的坐标
都是这个二元一次方程的解.
求自变量x为何值时,两
个函数的函数值相同.
解由两个含有未知数x、y的二元一次方程组成的二元一次方程组
从函数值看
归纳小结:
求两条相应直线的交点坐标.
从函数图象看
解由两个含有未知数x、y的二元一次方程组成的二元一次方程组
例1:当自变量x
取何值时,函数
的值为0?当自变量x
取何值时,函数
的值为
?
例1:当自变量x
取何值时,函数
的值为0?当自变量x
取何值时,函数
的值为
?
解法一:令
y=0,则
,解得
.
所以当
时,
的函数值是0.
令
,则
,解得
.
所以当
时,
的函数值是
.
例1:当自变量x
取何值时,函数
的值为0?当自变量x
取何值时,函数
的值为
?
解法二:画出直线
与x
轴交于
点
.
所以当
时,
函数值为
0
.
1
-1
-2
0
2
3
4
5
1
2
3
4
-1
-2
-3
x
y
例1:当自变量x
取何值时,函数
的值为0?当自变量x
取何值时,函数
的值为
?
解法二:当
时,直线
与
直线
相交于点
.
所以当
时,函数值为
.
1
-1
-2
0
2
3
4
5
1
2
3
4
-1
-2
-3
x
y
例2:当自变量x
取何值时,函数
与函数
的值相
等?这个函数值是多少?
例2:当自变量x
取何值时,函数
与函数
的值相
等?这个函数值是多少?
解法一:联立得到
,利用代入消元,将方程2代入方程1中,
得
,解得
.
所以当
时,两个函数函数值相同为
.
例2:当自变量x
取何值时,函数
与函数
的值相
等?这个函数值是多少?
解法二:
例2:当自变量x
取何值时,函数
与函数
的值相
等?这个函数值是多少?
解法二:
1
-1
-2
0
2
3
4
5
1
2
3
4
-1
-2
-3
x
y
例2:当自变量x
取何值时,函数
与函数
的值相
等?这个函数值是多少?
解法二:
1
-1
-2
0
2
3
4
5
1
2
3
4
-1
-2
-3
x
y
例2:当自变量x
取何值时,函数
与函数
的值相
等?这个函数值是多少?
解法二:直线
与直线
相交于点
.
1
-1
-2
0
2
3
4
5
1
2
3
4
-1
-2
-3
x
y
例2:当自变量x
取何值时,函数
与函数
的值相
等?这个函数值是多少?
解法二:直线
与直线
相交于点
.
这表示当
时,两个函数函数值相同
为
.
1
-1
-2
0
2
3
4
5
1
2
3
4
-1
-2
-3
x
y
例3:当函数
的值小于函数
的值时,求自变量x
取值范围.
例3:当函数
的值小于函数
的值时,求自变量x
取值范围.
解法一:
函数
的值小于函数
的值,
,
解得:
.
这表示当
时,函数
的值小于函
数
的值.
例3:当函数
的值小于函数
的值时,求自变量x
取值范围.
解法二:
例3:当函数
的值小于函数
的值时,求自变量x
取值范围.
解法二:
1
-1
-2
0
2
3
4
5
1
2
3
4
-1
-2
-3
x
y
例3:当函数
的值小于函数
的值时,求自变量x
取值范围.
解法二:从函数图象上看,在直线
右侧时,直线
在直线
的下方,所以当
时,函数
的值小于函
数
的值.
1
-1
-2
0
2
3
4
5
1
2
3
4
-1
-2
-3
x
y
5
-5
-10
0
10
15
20
5
10
15
-5
-10
x
y
例4:根据函数
的图象,确定x取何范围时,有:
(1)
;
(2)
.
5
-5
-10
0
10
15
20
5
10
15
-5
-10
x
y
例4:根据函数
的图象,确定x取何范围时,有:
(1)
;
(2)
.
5
-5
-10
0
10
15
20
5
10
15
-5
-10
x
y
解:(1)
函数值大
于0,也即直线在x轴上方.
例4:根据函数
的图象,确定x取何范围时,有:
(1)
;
(2)
.
5
-5
-10
0
10
15
20
5
10
15
-5
-10
x
y
解:(1)
函数值大
于0,也即直线在x轴上方.
此时
,
所以当
时
.
例4:根据函数
的图象,确定x取何范围时,有:
(1)
;
(2)
.
5
-5
-10
0
10
15
20
5
10
15
-5
-10
x
y
解:(2)
函数值小
于5,也即直线在
下
方.
例4:根据函数
的图象,确定x取何范围时,有:
(1)
;
(2)
.
5
-5
-10
0
10
15
20
5
10
15
-5
-10
x
y
解:(2)
函数值小
于5,也即直线在
下
方.此时
,所以当
时,
.
例4:根据函数
的图象,确定x取何范围时,有:
(1)
;
(2)
.
课堂总结:
课堂总结:
一次函数与一元一次方程之间的关系:
(1)解一元一次方程
相当于求一次函数
的值为c时,自变量x
的值,或求直线
上的点的纵坐标为c时横坐标x的值.
当
时,即求直线与x轴交点的横坐标的值.
课堂总结:
一次函数与一元一次不等式之间的关系:
(2)求
()
的解集相当于求一次函数
的值大于c(或大于等于c)时,自变量x
的取值范围,即确定直线
在
上方
(或上方含交点)时,自变量x
的取值范围.
课堂总结:
一次函数与一元一次不等式之间的关系:
(2)求
()
的解集相当于求一次函数
的值大于c(或大于等于c)时,自变量x
的取值范围,即确定直线
在
上方
(或上方含交点)时,自变量x
的取值范围.
请思考总结一元一次不等式
和
与一次函数之间的关系.
课堂总结:
一次函数二元一次方程(组)之间的关系:
(3)任何一个含有未知数x
和y
的二元一次方程都可以改写为
(k,b是常数,
)的形式,解由两个含有未知数的二元一次方程
组成的二元一次方程组相当于求自变量x为何值时,两个函数的函数值相
等,即确定两条相应直线的交点坐标.
课后作业:
考虑下面两种移动电话的计费方式:
方式一
方式二
月租费/(元/月)
30
0
本地通话费/(元/min)
0.30
0.40
用函数方法解答何时两种计费方式费用相等.
再
见
初二年级
数学
一次函数与方程、不等式
学习目标
1.理解一次函数与一元一次方程、
一元一次不等式、和二元一次方程(组)之间的关系.会用函数观点解释方程(组)和不等式及其解(解集)的意义.
2.经历用函数图象表示方程(组)、不等式的过程,进一步体会“以形表示数,以数解释形”的数形结合思想.
1、一次函数与一元一次方程:
问题1.
下面3个方程有什么共同点和不同点?你能从函数的角度
对解这3个方程进行解释吗?
(1)
;(2)
;(3)
.
1、一次函数与一元一次方程:
问题1.
下面3个方程有什么共同点和不同点?你能从函数的角度
对解这3个方程进行解释吗?
(1)
;(2)
;(3)
.
相同之处:这3个方程等号的左边都是
;
不同之处:等号右边分别为
3、0、-1.
用函数观点看方程
(1)
;(2)
;(3)
.
用函数观点看方程
(1)
;(2)
;(3)
.
1
-1
-2
0
2
3
4
1
2
3
4
5
-1
-2
-3
x
y
用函数观点看方程
(1)
;(2)
;(3)
.
1
-1
-2
0
2
3
4
1
2
3
4
5
-1
-2
-3
x
y
的解
解一元一次方程
表示求函
数
的函数值为3时,自变
量x的值,或求直线
上的
点纵坐标为3时,横坐标的值.
此
时
,这是
的解
.
用函数观点看方程
(1)
;(2)
;(3)
.
1
-1
-2
0
2
3
4
1
2
3
4
5
-1
-2
-3
x
y
的解
(2)解一元一次方程
表示求函
数
的函数值为0时,自变
量x的值,或求直线
与
x
轴交点的横坐标的值.
此时
,
这是
的解
.
用函数观点看方程
(1)
;(2)
;(3)
.
1
-1
-2
0
2
3
4
1
2
3
4
5
-1
-2
-3
x
y
的解
(3)解一元一次方程
表示求函
数
的函数值为-1时,自变
量x的值,或求直线
上的点
纵坐标为-1时,横坐标的值.
此时
,这是
的解.
用函数观点看方程
(1)
;(2)
;(3)
.
1
-1
-2
0
2
3
4
1
2
3
4
5
-1
-2
-3
x
y
的解
的解
的解
解一元一次方程
表
示求函数
的函数值为c
时,
自变量x的值,或求直线
上的点纵坐标为c
时,横坐标的值.
思考:请结合函数图象填空并解下列关于x的一元一次方程:
(1)
;
(2)
;(3)
.
1
-1
-2
0
2
3
4
1
2
3
4
5
-1
-2
-3
x
y
5
思考:请结合函数图象填空并解下列关于x的一元一次方程:
(1)
;
(2)
;(3)
.
1
-1
-2
0
2
3
4
1
2
3
4
5
-1
-2
-3
x
y
5
(1)解方程
表示求函数__________
的函数值为_5_时,自变量x的取值,也即
求直线__________上的点纵坐标为_5_时,
横坐标x的取值.
因此方程
的
解为_______.
1
-1
-2
0
2
3
4
1
2
3
4
5
-1
-2
-3
x
y
5
(2)解方程
表示求函数__________
的函数值为_0_时,自变量x的取值,也即
求直线__________与x轴交点的_横坐标
的
值.
因此方程
的解为_______.
思考:请结合函数图象填空并解下列关于x的一元一次方程:
(1)
;
(2)
;(3)
.
1
-1
-2
0
2
3
4
1
2
3
4
5
-1
-2
-3
x
y
5
(3)解方程
表示求函数__________
的函数值为_-1_时,自变量x的取值,也即
求直线__________上的点纵坐标为_-1_时,
横坐标x的取值.
因此方程
的
解为_______.
思考:请结合函数图象填空并解下列关于x的一元一次方程:
(1)
;
(2)
;(3)
.
思考:请结合函数图象填空并解下列关于x的一元一次方程:
(1)
;
(2)
;(3)
.
1
-1
-2
0
2
3
4
1
2
3
4
5
-1
-2
-3
x
y
5
解一元一次方程
表
示求函数
的函数值为c时,
自变量x的值,或求直线
上的点纵坐标为c
时,横坐标的值.
归纳小结:
归纳小结:
从函数的概念的角度来理解一元一次方程
的解,它是函数
在随自变量x变化过程中的一个状态,也就是函数值为c时的这个状态.
归纳小结:
从函数的概念的角度来理解一元一次方程
的解,它是函数
在随自变量x变化过程中的一个状态,也就是函数值为c时的这个状态.
求一元一次方程
的解.
求一次函数
的值为c时,对应的自变量x
的值.
从函数值看
1
-1
-2
0
2
3
4
1
2
3
4
5
-1
-2
-3
x
y
的解
的解
的解
求一元一次方程
的解.
求直线
上的点的纵坐标为c时横坐标x的值;当
时,即求直线与x轴交点的横坐标的值.
从函数图象看
2、一次函数与一元一次不等式:
问题2.
下面3个不等式有什么共同点和不同点?你能从函数的角
度对解这3个不等式进行解释吗?
(1)
;(2)
;(3)
.
2、一次函数与一元一次不等式:
相同之处:这3个不等式的不等号左边都是
不同之处:不等号及不等号右边不同.
问题2.
下面3个不等式有什么共同点和不同点?你能从函数的角
度对解这3个不等式进行解释吗?
(1)
;(2)
;(3)
.
用函数观点看下列不等式:
,
,
,
.
上述四个不等式的解集共用一个临界值
时,自变量的取值.
用函数观点看下列不等式:
,
,
,
.
1
-1
-2
0
2
3
4
1
2
3
4
-1
-2
-3
x
y
5
用函数观点看下列不等式:
,
,
,
.
1
-1
-2
0
2
3
4
1
2
3
4
-1
-2
-3
x
y
5
解
表示求函数
的函数值
大于5时,或求直线
在直线
的
上方时,自变量x的取值范围.
用函数观点看下列不等式:
,
,
,
.
1
-1
-2
0
2
3
4
1
2
3
4
-1
-2
-3
x
y
5
解
表示求函数
的函数值
大于5时,或求直线
在直线
的
上方时,自变量x的取值范围.所以
的解集为
.
用函数观点看下列不等式:
,
,
,
.
1
-1
-2
0
2
3
4
1
2
3
4
-1
-2
-3
x
y
5
解
表示求函数
的函数值
小于5时,或求直线
在直线
的
下方时,自变量x的取值范围.所以
的解集为
.
用函数观点看下列不等式:
,
,
,
.
1
-1
-2
0
2
3
4
1
2
3
4
-1
-2
-3
x
y
5
解
表示求函数
的函数值
大于等于5时,或求直线
在直线
的上方含交点时,自变量x的取值范
围.所以
的解集为
.
用函数观点看下列不等式:
,
,
,
.
1
-1
-2
0
2
3
4
1
2
3
4
-1
-2
-3
x
y
5
解
表示求函数
的函数值
小于等于5时,或求直线
在直线
的下方含交点时,自变量x的取值范
围.所以
的解集为
.
用函数观点看不等式
(2)
;
(3)
.
1
-1
-2
0
2
3
4
1
2
3
4
-1
-2
-3
x
y
5
用函数观点看不等式
(2)
;
(3)
.
1
-1
-2
0
2
3
4
1
2
3
4
-1
-2
-3
x
y
5
(2)解
表示求函数
的函数
值小于0时,或求直线
在x轴下
方时,自变量x的取值范围.所以
的解集为
.
用函数观点看不等式
(2)
;
(3)
.
1
-1
-2
0
2
3
4
1
2
3
4
-1
-2
-3
x
y
5
(3)解
表示求函数
的函
数值大于-1时,或求直线
在
上方时,自变量x的取值范围.所
以
的解集为
.
解一元一次不等式
就是求当函数
的函数值值大于c(小于c)时,或求直线
在直线
上方(或下方)时,自变量x
的取值范围.
用函数观点看解不等式:
(1)
;(2)
;(3)
.
归纳小结:
归纳小结:
从函数的概念的角度来理解一元一次不等式
(
)(
)
的解集,它是函数
在随自变量x变化过程中的一段状态,也就是函数值大于c(或大于等于c
)时的这段状态.
归纳小结:
从函数的概念的角度来理解一元一次不等式
(
)(
)
的解集,它是函数
在随自变量x变化过程中的一段状态,也就是函数值大于c(或大于等于c
)时的这段状态.
求一次函数
的值大于c(大于等于c)时,自变量x
的取值范围.
从函数值看
求
(
)
(
)
的解集.
确定直线
在
上方
(上方含交点)时,自变量x
的取值范围.
当
时,
为x轴.
从函数图象看
求
(
)
(
)
的解集.
确定直线
在
上方
(上方含交点)时,自变量x
的取值范围.
当
时,
为x轴.
从函数图象看
求
(
)
(
)
的解集.
请思考总结如何从函数值和函数图象两个角度来解释求一元一次不等式
和
吗?
3、一次函数与二元一次方程:
问题3.
1号探测气球从海拔5m处出发,以1m/min的速度上升.与此同时,2号探测气球从海拔15m处出发,以0.5m/min的速度上升.
两个气球都上升了1h.
(1)
请用解析式分别表示两个气球所在位置的海
拔y(单位:m)与气球上升时间x(单位:min)
的函数关系.
3、一次函数与二元一次方程:
问题3.
1号探测气球从海拔5m处出发,以1m/min的速度上升.与此同时,2号探测气球从海拔15m处出发,以0.5m/min的速度上升.
两个气球都上升了1h.
(1)
请用解析式分别表示两个气球所在位置的海
拔y(单位:m)与气球上升时间x(单位:min)
的函数关系.
气球1
海拔高度:
;
3、一次函数与二元一次方程:
问题3.
1号探测气球从海拔5m处出发,以1m/min的速度上升.与此同时,2号探测气球从海拔15m处出发,以0.5m/min的速度上升.
两个气球都上升了1h.
(1)
请用解析式分别表示两个气球所在位置的海
拔y(单位:m)与气球上升时间x(单位:min)
的函数关系.
气球1
海拔高度:
;
气球2
海拔高度:
.
(2)
在某时刻两个气球能否位于同一高度?如果能,这时气球上升了多
长时间?位于什么高度?
(2)
在某时刻两个气球能否位于同一高度?如果能,这时气球上升了多
长时间?位于什么高度?
解得:
从二元一次方程组(数)的角度:
当上升20min时,两个气球都位于海拔25m高度.
从一次函数图象(形)的角度:
从一次函数图象(形)的角度:
y
x
10
20
15
5
30
25
20
15
10
5
O
/min
/m
从一次函数图象(形)的角度:
y
x
10
20
15
5
30
25
20
15
10
5
O
/min
/m
从一次函数图象(形)的角度:
这表示当20min时,气球1和气球2都位于海拔25m的高度.
y
x
10
20
15
5
30
25
20
15
10
5
O
/min
/m
归纳小结:
归纳小结:
任何一个含有未知数x
和y
的二元一次方程都可以改写为
(k,b是常数,
)的形式,所以每一个这样的方程都对应着一个一次函数,于是也对应一条直线.
直线上每一个点的坐标
都是这个二元一次方程的解.
归纳小结:
任何一个含有未知数x
和y
的二元一次方程都可以改写为
(k,b是常数,
)的形式,所以每一个这样的方程都对应着一个一次函数,于是也对应一条直线.
直线上每一个点的坐标
都是这个二元一次方程的解.
求自变量x为何值时,两
个函数的函数值相同.
解由两个含有未知数x、y的二元一次方程组成的二元一次方程组
从函数值看
归纳小结:
求两条相应直线的交点坐标.
从函数图象看
解由两个含有未知数x、y的二元一次方程组成的二元一次方程组
例1:当自变量x
取何值时,函数
的值为0?当自变量x
取何值时,函数
的值为
?
例1:当自变量x
取何值时,函数
的值为0?当自变量x
取何值时,函数
的值为
?
解法一:令
y=0,则
,解得
.
所以当
时,
的函数值是0.
令
,则
,解得
.
所以当
时,
的函数值是
.
例1:当自变量x
取何值时,函数
的值为0?当自变量x
取何值时,函数
的值为
?
解法二:画出直线
与x
轴交于
点
.
所以当
时,
函数值为
0
.
1
-1
-2
0
2
3
4
5
1
2
3
4
-1
-2
-3
x
y
例1:当自变量x
取何值时,函数
的值为0?当自变量x
取何值时,函数
的值为
?
解法二:当
时,直线
与
直线
相交于点
.
所以当
时,函数值为
.
1
-1
-2
0
2
3
4
5
1
2
3
4
-1
-2
-3
x
y
例2:当自变量x
取何值时,函数
与函数
的值相
等?这个函数值是多少?
例2:当自变量x
取何值时,函数
与函数
的值相
等?这个函数值是多少?
解法一:联立得到
,利用代入消元,将方程2代入方程1中,
得
,解得
.
所以当
时,两个函数函数值相同为
.
例2:当自变量x
取何值时,函数
与函数
的值相
等?这个函数值是多少?
解法二:
例2:当自变量x
取何值时,函数
与函数
的值相
等?这个函数值是多少?
解法二:
1
-1
-2
0
2
3
4
5
1
2
3
4
-1
-2
-3
x
y
例2:当自变量x
取何值时,函数
与函数
的值相
等?这个函数值是多少?
解法二:
1
-1
-2
0
2
3
4
5
1
2
3
4
-1
-2
-3
x
y
例2:当自变量x
取何值时,函数
与函数
的值相
等?这个函数值是多少?
解法二:直线
与直线
相交于点
.
1
-1
-2
0
2
3
4
5
1
2
3
4
-1
-2
-3
x
y
例2:当自变量x
取何值时,函数
与函数
的值相
等?这个函数值是多少?
解法二:直线
与直线
相交于点
.
这表示当
时,两个函数函数值相同
为
.
1
-1
-2
0
2
3
4
5
1
2
3
4
-1
-2
-3
x
y
例3:当函数
的值小于函数
的值时,求自变量x
取值范围.
例3:当函数
的值小于函数
的值时,求自变量x
取值范围.
解法一:
函数
的值小于函数
的值,
,
解得:
.
这表示当
时,函数
的值小于函
数
的值.
例3:当函数
的值小于函数
的值时,求自变量x
取值范围.
解法二:
例3:当函数
的值小于函数
的值时,求自变量x
取值范围.
解法二:
1
-1
-2
0
2
3
4
5
1
2
3
4
-1
-2
-3
x
y
例3:当函数
的值小于函数
的值时,求自变量x
取值范围.
解法二:从函数图象上看,在直线
右侧时,直线
在直线
的下方,所以当
时,函数
的值小于函
数
的值.
1
-1
-2
0
2
3
4
5
1
2
3
4
-1
-2
-3
x
y
5
-5
-10
0
10
15
20
5
10
15
-5
-10
x
y
例4:根据函数
的图象,确定x取何范围时,有:
(1)
;
(2)
.
5
-5
-10
0
10
15
20
5
10
15
-5
-10
x
y
例4:根据函数
的图象,确定x取何范围时,有:
(1)
;
(2)
.
5
-5
-10
0
10
15
20
5
10
15
-5
-10
x
y
解:(1)
函数值大
于0,也即直线在x轴上方.
例4:根据函数
的图象,确定x取何范围时,有:
(1)
;
(2)
.
5
-5
-10
0
10
15
20
5
10
15
-5
-10
x
y
解:(1)
函数值大
于0,也即直线在x轴上方.
此时
,
所以当
时
.
例4:根据函数
的图象,确定x取何范围时,有:
(1)
;
(2)
.
5
-5
-10
0
10
15
20
5
10
15
-5
-10
x
y
解:(2)
函数值小
于5,也即直线在
下
方.
例4:根据函数
的图象,确定x取何范围时,有:
(1)
;
(2)
.
5
-5
-10
0
10
15
20
5
10
15
-5
-10
x
y
解:(2)
函数值小
于5,也即直线在
下
方.此时
,所以当
时,
.
例4:根据函数
的图象,确定x取何范围时,有:
(1)
;
(2)
.
课堂总结:
课堂总结:
一次函数与一元一次方程之间的关系:
(1)解一元一次方程
相当于求一次函数
的值为c时,自变量x
的值,或求直线
上的点的纵坐标为c时横坐标x的值.
当
时,即求直线与x轴交点的横坐标的值.
课堂总结:
一次函数与一元一次不等式之间的关系:
(2)求
()
的解集相当于求一次函数
的值大于c(或大于等于c)时,自变量x
的取值范围,即确定直线
在
上方
(或上方含交点)时,自变量x
的取值范围.
课堂总结:
一次函数与一元一次不等式之间的关系:
(2)求
()
的解集相当于求一次函数
的值大于c(或大于等于c)时,自变量x
的取值范围,即确定直线
在
上方
(或上方含交点)时,自变量x
的取值范围.
请思考总结一元一次不等式
和
与一次函数之间的关系.
课堂总结:
一次函数二元一次方程(组)之间的关系:
(3)任何一个含有未知数x
和y
的二元一次方程都可以改写为
(k,b是常数,
)的形式,解由两个含有未知数的二元一次方程
组成的二元一次方程组相当于求自变量x为何值时,两个函数的函数值相
等,即确定两条相应直线的交点坐标.
课后作业:
考虑下面两种移动电话的计费方式:
方式一
方式二
月租费/(元/月)
30
0
本地通话费/(元/min)
0.30
0.40
用函数方法解答何时两种计费方式费用相等.
再
见
