等腰三角形
图片预览

文档简介
(共17张PPT)
营山县三元小学 余志明
等腰三角形
九年义务教育八年级数学上册
等腰三角形
10
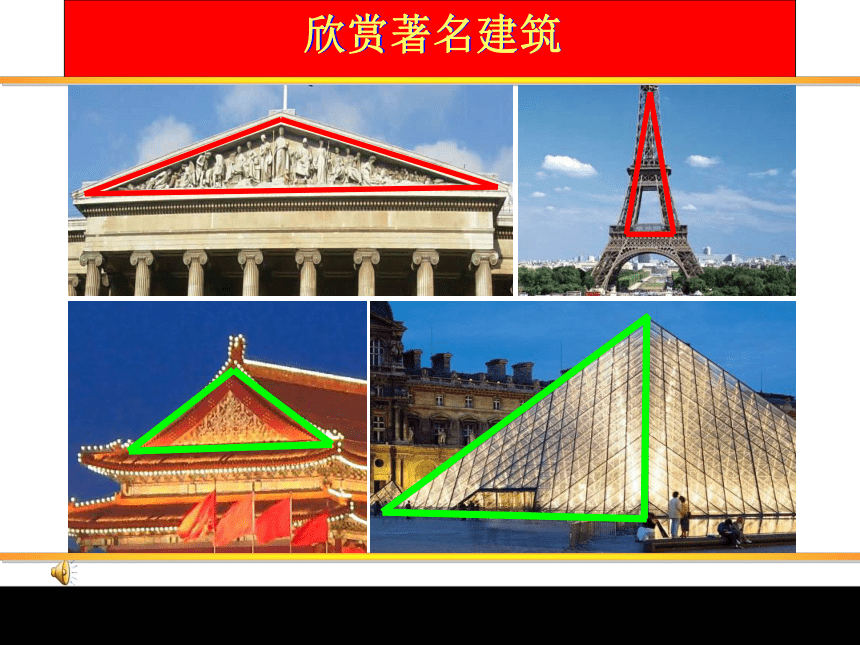
欣赏著名建筑
北京天安门
埃菲儿铁塔
巴黎卢浮宫
伦敦白金汉宫
欣赏著名建筑
A
B
C
底边
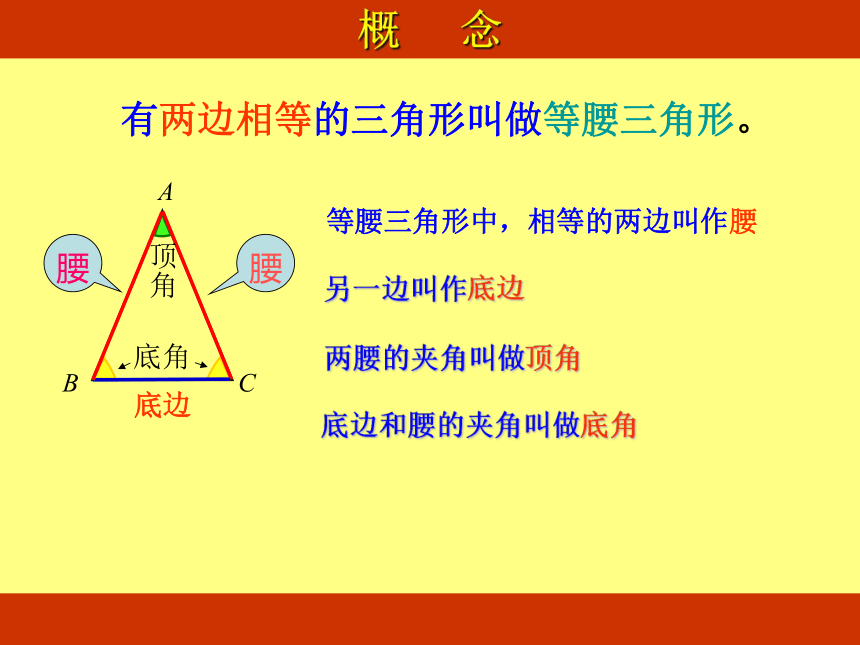
顶角
底角
等腰三角形中,相等的两边叫作腰
两腰的夹角叫做顶角
底边和腰的夹角叫做底角
有两边相等的三角形叫做等腰三角形。
概 念
腰
腰
另一边叫作底边
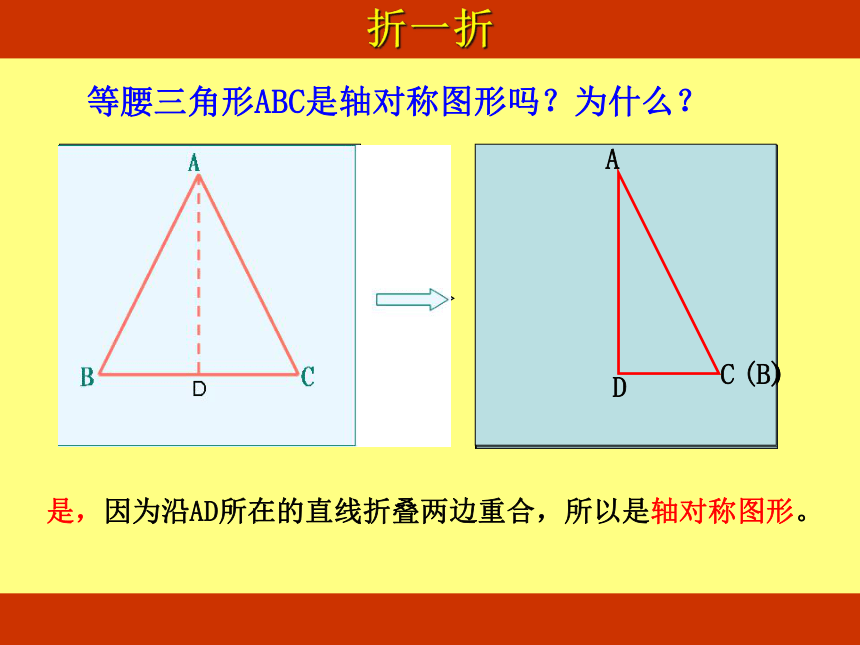
等腰三角形ABC是轴对称图形吗?为什么?
是,因为沿AD所在的直线折叠两边重合,所以是轴对称图形。
A
C
B
A
C
B
B
A
C
B
A
C
A
C
B
A
C
B
A
C
B
B
A
C
(B)
A
C
B
A
C
A
C
B
A
C
B
A
C
B
B
A
C
B
A
C
A
C
B
A
C
B
A
C
B
B
A
C
B
A
C
A
C
B
A
C
B
A
C
B
B
A
C
(B)
A
C
(B)
A
C
A
C
B
折一折
D
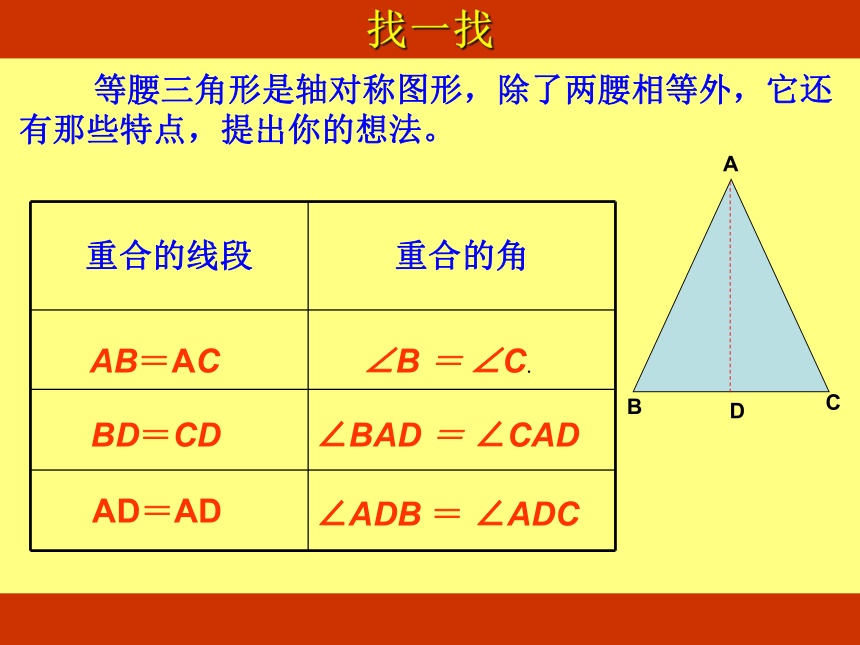
重合的线段 重合的角
A
C
B
D
AB=AC
BD=CD
AD=AD
∠B = ∠C.
∠BAD = ∠CAD
∠ADB = ∠ADC
找一找
等腰三角形是轴对称图形,除了两腰相等外,它还有那些特点,提出你的想法。
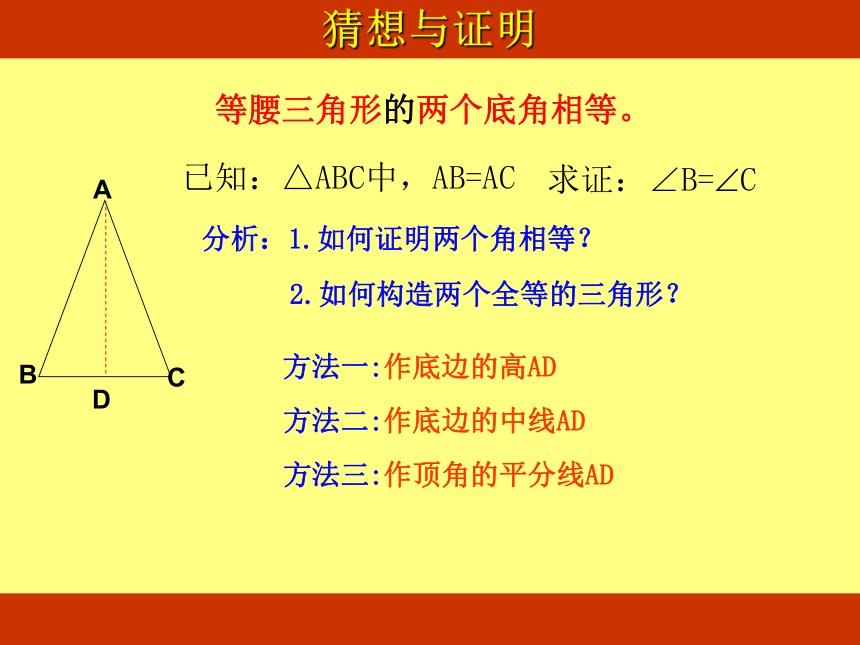
等腰三角形的两个底角相等。
已知:△ABC中,AB=AC
求证:∠B= C
分析:1.如何证明两个角相等?
2.如何构造两个全等的三角形?
A
B
C
D
猜想与证明
方法一:作底边的高AD
方法二:作底边的中线AD
方法三:作顶角的平分线AD
D
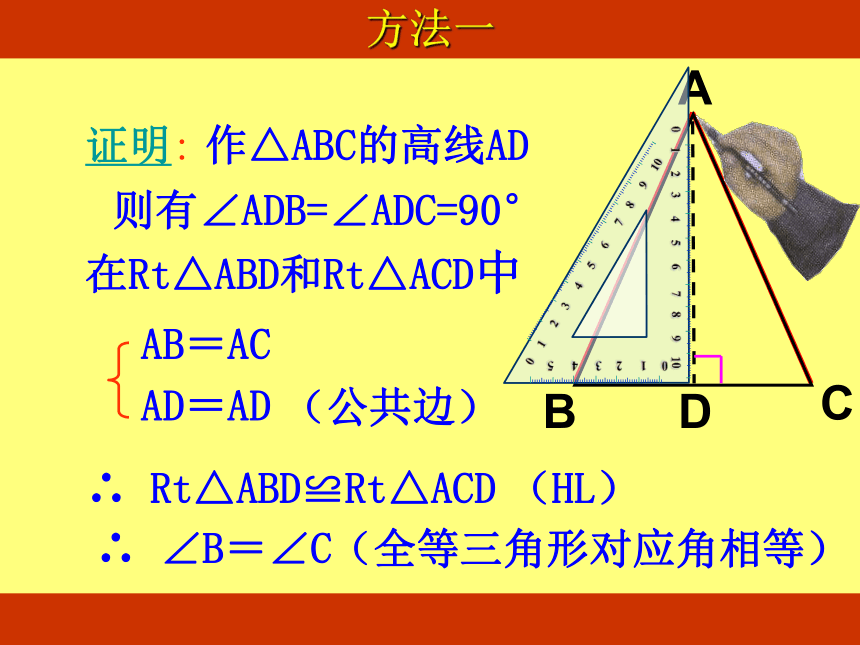
在Rt△ABD和Rt△ACD中
AB=AC
AD=AD
(公共边)
∴ Rt△ABD≌Rt△ACD
(HL)
∴ ∠B=∠C
(全等三角形对应角相等)
证明: 作△ABC的高线AD
方法一
则有∠ADB=∠ADC=90°
A
B
C
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
A
B
C
D
在△ABD和△ACD中
AB=AC
BD=CD
AD=AD
(公共边)
∴ △ABD≌△ACD
(SSS)
∴ ∠B=∠C
(全等三角形对应角相等)
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
证明: 作△ABC的中线AD
则有BD=CD
方法二
A
B
C
D
1
2
在△ABD和△ACD中
AB=AC
∠1=∠2
AD=AD
(公共边)
∴ △ABD≌△ACD
(SAS)
∴ ∠B=∠C
(全等三角形对应角相等)
则∠1=∠2
证明: 作顶角的平分线AD,
方法三
性质1:等腰三角形的两个底角相等(简写成“等边对等角”).
A
B
C
在△ABC中,
∵AB=AC(已知)
∴∠B =∠C(等边对等角)
用符号语言表示为:
等腰三角形的性质一
(等腰三角形底边上的中线平分顶角并且垂直于底边.)
(等腰三角形顶角的平分线平分底边并且垂直于底边.)
∵AD是∠BAC的平分线∴ ⊥ , = 。
(等腰三角形底边上的高平分顶角并且平分底边.)
∵AD ⊥ BC ∴∠ = ∠ , = 。
∵AD是底边BC的中线∴ ⊥ ,∠ =∠ 。
用符号语言表示为:
性质2:等腰三角形顶角平分线、底边上的中线、底边上的高相互重合.(简写成“三线合一”)
在△ABC中,AB =AC, 点 D在BC上
1
2
BD
CD
AD
BC
1
2
AD
BC
BD
CD
`
A
B
D
C
1
2
等腰三角形的性质二
在等腰三角形中,顶角平分线,底边上的中线,底边上的高有一个成立,其余两个也同时成立。
⒈等腰三角形一个顶角为80°,它的另外两个
角为___________________ ;
⒉等腰三角形一个角为80°,它的另外两个角
为____________________________ ;
⒊等腰三角形一个角为120°,它的另外两个角
为___________________ 。
50°, 50°
50°, 50°或80°, 20°
30°, 30°
小试牛刀
想一想:
等腰三角形的底角可以是直角或钝角吗?为什么?
顶角= -2×底角
<顶角<180°
<底角<90°
180°
0°
0°
( )(1)等腰三角形的角平分线、中线和高相互重合.
( )(2)等腰三角形底边上的高就是顶角的平分线.
( )(3)等腰三角形是轴对称图形,共有3条对称轴.
×
√
×
再创佳绩
A
B
C
D
例题:如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,
解:设∠A=X,
∴ ∠BDC=∠C=∠ABC=2X,
∴ ∠A=∠ABD=X
又∵BD=BC AB=AC,
∴ ∠BDC=∠A+∠ABD=2X,
于是在△ABC中,有
∠A+∠ABC+∠C=X+2X+2X=180°
解得X=36°.
在△ABC中,∠A=36°,∠ABC=∠C=72°.
x
x
2x
2x
2x
问题一:由条件,你能在图中找出几个等腰三角形?
分析:
三个等腰三角形:
△ABC、 △ABD、 △BDC
问题二:因此,你能在找出那些相等的角?它们之间有何关系?
问题三:你用什么方法能快速地表达出图中各角之间的关系?
用设未知数列方程的方法,即方程思想来解决。
∵ AD=BD
∠1=∠2 ∠3=∠5=∠4
∠3=∠5=∠4= 2∠1=2∠2
例题讲解
求△ABC各角的度数。
1
2
3
5
4
1
2
3
x
我的收获
我有哪些收获?
等腰三角形的概念
等腰三角形的性质
利用等腰三角形的性质解题
本节课你有哪些收获?有何感想?
作 业
1.必做题:教科书第51页练习1、2、3,第56页习
题12.3第6题;
2.选做题:教科书第56页习题12.3第1、3题.
营山县三元小学 余志明
谢 谢 大 家
谢 谢 大 家
营山县三元小学 余志明
等腰三角形
九年义务教育八年级数学上册
等腰三角形
10
欣赏著名建筑
北京天安门
埃菲儿铁塔
巴黎卢浮宫
伦敦白金汉宫
欣赏著名建筑
A
B
C
底边
顶角
底角
等腰三角形中,相等的两边叫作腰
两腰的夹角叫做顶角
底边和腰的夹角叫做底角
有两边相等的三角形叫做等腰三角形。
概 念
腰
腰
另一边叫作底边
等腰三角形ABC是轴对称图形吗?为什么?
是,因为沿AD所在的直线折叠两边重合,所以是轴对称图形。
A
C
B
A
C
B
B
A
C
B
A
C
A
C
B
A
C
B
A
C
B
B
A
C
(B)
A
C
B
A
C
A
C
B
A
C
B
A
C
B
B
A
C
B
A
C
A
C
B
A
C
B
A
C
B
B
A
C
B
A
C
A
C
B
A
C
B
A
C
B
B
A
C
(B)
A
C
(B)
A
C
A
C
B
折一折
D
重合的线段 重合的角
A
C
B
D
AB=AC
BD=CD
AD=AD
∠B = ∠C.
∠BAD = ∠CAD
∠ADB = ∠ADC
找一找
等腰三角形是轴对称图形,除了两腰相等外,它还有那些特点,提出你的想法。
等腰三角形的两个底角相等。
已知:△ABC中,AB=AC
求证:∠B= C
分析:1.如何证明两个角相等?
2.如何构造两个全等的三角形?
A
B
C
D
猜想与证明
方法一:作底边的高AD
方法二:作底边的中线AD
方法三:作顶角的平分线AD
D
在Rt△ABD和Rt△ACD中
AB=AC
AD=AD
(公共边)
∴ Rt△ABD≌Rt△ACD
(HL)
∴ ∠B=∠C
(全等三角形对应角相等)
证明: 作△ABC的高线AD
方法一
则有∠ADB=∠ADC=90°
A
B
C
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
A
B
C
D
在△ABD和△ACD中
AB=AC
BD=CD
AD=AD
(公共边)
∴ △ABD≌△ACD
(SSS)
∴ ∠B=∠C
(全等三角形对应角相等)
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
证明: 作△ABC的中线AD
则有BD=CD
方法二
A
B
C
D
1
2
在△ABD和△ACD中
AB=AC
∠1=∠2
AD=AD
(公共边)
∴ △ABD≌△ACD
(SAS)
∴ ∠B=∠C
(全等三角形对应角相等)
则∠1=∠2
证明: 作顶角的平分线AD,
方法三
性质1:等腰三角形的两个底角相等(简写成“等边对等角”).
A
B
C
在△ABC中,
∵AB=AC(已知)
∴∠B =∠C(等边对等角)
用符号语言表示为:
等腰三角形的性质一
(等腰三角形底边上的中线平分顶角并且垂直于底边.)
(等腰三角形顶角的平分线平分底边并且垂直于底边.)
∵AD是∠BAC的平分线∴ ⊥ , = 。
(等腰三角形底边上的高平分顶角并且平分底边.)
∵AD ⊥ BC ∴∠ = ∠ , = 。
∵AD是底边BC的中线∴ ⊥ ,∠ =∠ 。
用符号语言表示为:
性质2:等腰三角形顶角平分线、底边上的中线、底边上的高相互重合.(简写成“三线合一”)
在△ABC中,AB =AC, 点 D在BC上
1
2
BD
CD
AD
BC
1
2
AD
BC
BD
CD
`
A
B
D
C
1
2
等腰三角形的性质二
在等腰三角形中,顶角平分线,底边上的中线,底边上的高有一个成立,其余两个也同时成立。
⒈等腰三角形一个顶角为80°,它的另外两个
角为___________________ ;
⒉等腰三角形一个角为80°,它的另外两个角
为____________________________ ;
⒊等腰三角形一个角为120°,它的另外两个角
为___________________ 。
50°, 50°
50°, 50°或80°, 20°
30°, 30°
小试牛刀
想一想:
等腰三角形的底角可以是直角或钝角吗?为什么?
顶角= -2×底角
<顶角<180°
<底角<90°
180°
0°
0°
( )(1)等腰三角形的角平分线、中线和高相互重合.
( )(2)等腰三角形底边上的高就是顶角的平分线.
( )(3)等腰三角形是轴对称图形,共有3条对称轴.
×
√
×
再创佳绩
A
B
C
D
例题:如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,
解:设∠A=X,
∴ ∠BDC=∠C=∠ABC=2X,
∴ ∠A=∠ABD=X
又∵BD=BC AB=AC,
∴ ∠BDC=∠A+∠ABD=2X,
于是在△ABC中,有
∠A+∠ABC+∠C=X+2X+2X=180°
解得X=36°.
在△ABC中,∠A=36°,∠ABC=∠C=72°.
x
x
2x
2x
2x
问题一:由条件,你能在图中找出几个等腰三角形?
分析:
三个等腰三角形:
△ABC、 △ABD、 △BDC
问题二:因此,你能在找出那些相等的角?它们之间有何关系?
问题三:你用什么方法能快速地表达出图中各角之间的关系?
用设未知数列方程的方法,即方程思想来解决。
∵ AD=BD
∠1=∠2 ∠3=∠5=∠4
∠3=∠5=∠4= 2∠1=2∠2
例题讲解
求△ABC各角的度数。
1
2
3
5
4
1
2
3
x
我的收获
我有哪些收获?
等腰三角形的概念
等腰三角形的性质
利用等腰三角形的性质解题
本节课你有哪些收获?有何感想?
作 业
1.必做题:教科书第51页练习1、2、3,第56页习
题12.3第6题;
2.选做题:教科书第56页习题12.3第1、3题.
营山县三元小学 余志明
谢 谢 大 家
谢 谢 大 家
