人教版九年级下册数学 28.1锐角三角函数 ——特殊角的三角函数值课件 (共18张PPT)
文档属性
| 名称 | 人教版九年级下册数学 28.1锐角三角函数 ——特殊角的三角函数值课件 (共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 530.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-20 10:03:51 | ||
图片预览




文档简介
(共19张PPT)
新人教版九年级数学(下册)第二十八章
28.1锐角三角函数(3)
——特殊角的三角函数值
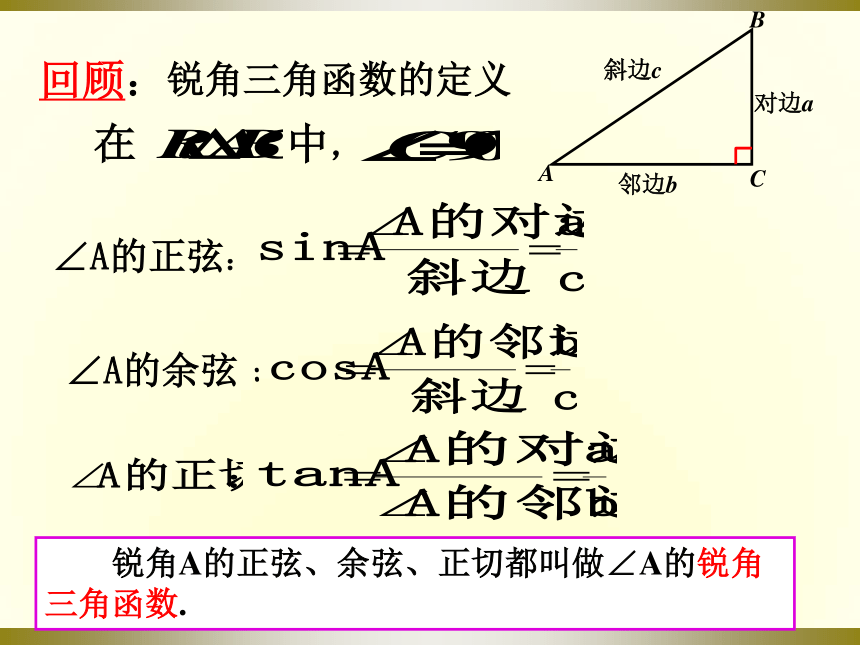
回顾:
锐角三角函数的定义
在
中,
∠A的余弦
:
∠A的正弦:
锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数.
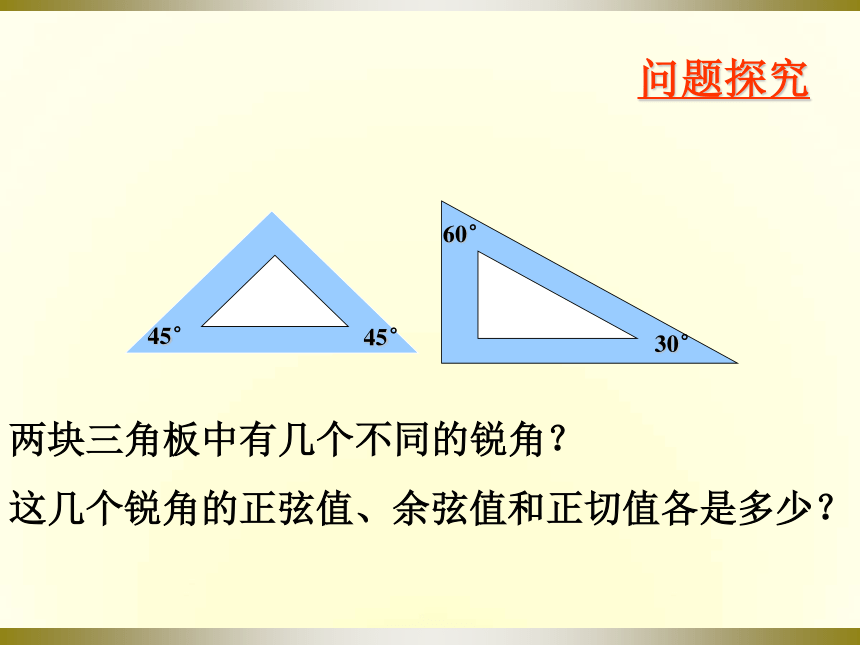
两块三角板中有几个不同的锐角?
这几个锐角的正弦值、余弦值和正切值各是多少?
30°
60°
45°
45°
问题探究
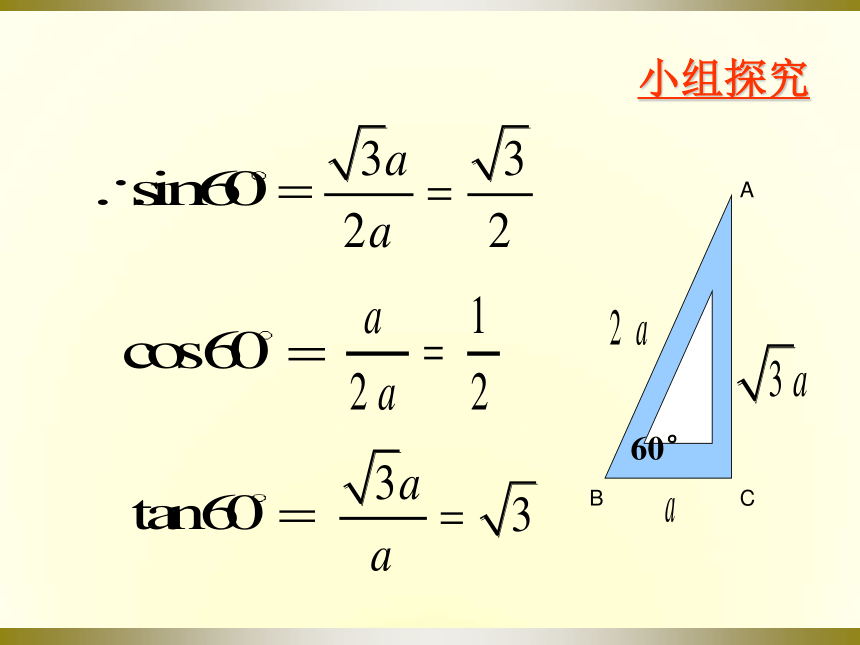
设30°所对的直角边长为a,那么斜边长为2a
另一条直角边长=
问题探究
A
B
C
30°
小组探究
A
B
C
设两条直角边长为a,
则斜边长=
45°
小组探究
A
B
C
┌
┌
300
600
450
a
a
a
2a
┌
a
2a
特殊角的三角函数值
活动成果
三角函数
锐角α
300
450
600
sin
α
cos
α
tan
α
sin45°=
cos30°=
tan30°=
cos60°=
cos45°=
tan45°=
tan60°=
1
sin30°=
例1
求下列各式的值:
(1)cos260°+sin260°
(2)
求下列各式的值:
(1)1-2
sin30°cos30°
(2)3tan30°-tan45°+2sin60°
解:
(1)1-2
sin30°cos30°
(2)3tan30°-tan45°+2sin60°
巩固训练
(1)若∠A是锐角,sinA=
,则∠A=(
)
(2)若∠C是锐角,tanC=
,
则∠C
=(
)
600
300
反过来,由锐角的三角函数值求锐角的度数
由锐角的三角函数值反求锐角(逆向思维)
∠A=
∠A=
∠A=
∠A=
∠A=
∠A=
∠A=
∠A=
∠A=
例2
(1)如图,在Rt△ABC中,∠C=90°,
,
求∠A的度数.
解:
在Rt△ABC中,∠C=90°
应用新知
(2)如图,AO是圆锥的高,OB是底面半径,
AO=
OB
倍,求
a
的度数.
解:在Rt△AOB中,∠
AOB
=90°
A
B
O
当A,B为锐角
时,若A≠B,则
sinA≠sinB,
cosA≠cosB,
tanA≠tanB.
在Rt△ABC中,∠C=90°,
求∠A、∠B的度数.(课本67页第2题)
B
A
C
∴
∠
A=30°
∠B
=
90°-
∠
A
=
90°-30°=
60°
解:在Rt△
ABC中,∠C=90°
巩固训练
1.
cos30°=(
)
2.
计算
2sin45°的结果等于(
)
3.计算:
【解析】
随堂练习
A.
B.
C.
D.
A.
B.
C.
D.
C
A
30°、45°、60°角的正弦值、余弦值和正切值如下表:
对于sinα与tanα,角度越大,函数值也越大;
对于cosα,角度越大,函数值越小。
课堂小结
锐角a
三角函数
30°
45°
60°
sin
a
cos
a
tan
a
课本69页
练习第3题
课堂作业
新人教版九年级数学(下册)第二十八章
28.1锐角三角函数(3)
——特殊角的三角函数值
回顾:
锐角三角函数的定义
在
中,
∠A的余弦
:
∠A的正弦:
锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数.
两块三角板中有几个不同的锐角?
这几个锐角的正弦值、余弦值和正切值各是多少?
30°
60°
45°
45°
问题探究
设30°所对的直角边长为a,那么斜边长为2a
另一条直角边长=
问题探究
A
B
C
30°
小组探究
A
B
C
设两条直角边长为a,
则斜边长=
45°
小组探究
A
B
C
┌
┌
300
600
450
a
a
a
2a
┌
a
2a
特殊角的三角函数值
活动成果
三角函数
锐角α
300
450
600
sin
α
cos
α
tan
α
sin45°=
cos30°=
tan30°=
cos60°=
cos45°=
tan45°=
tan60°=
1
sin30°=
例1
求下列各式的值:
(1)cos260°+sin260°
(2)
求下列各式的值:
(1)1-2
sin30°cos30°
(2)3tan30°-tan45°+2sin60°
解:
(1)1-2
sin30°cos30°
(2)3tan30°-tan45°+2sin60°
巩固训练
(1)若∠A是锐角,sinA=
,则∠A=(
)
(2)若∠C是锐角,tanC=
,
则∠C
=(
)
600
300
反过来,由锐角的三角函数值求锐角的度数
由锐角的三角函数值反求锐角(逆向思维)
∠A=
∠A=
∠A=
∠A=
∠A=
∠A=
∠A=
∠A=
∠A=
例2
(1)如图,在Rt△ABC中,∠C=90°,
,
求∠A的度数.
解:
在Rt△ABC中,∠C=90°
应用新知
(2)如图,AO是圆锥的高,OB是底面半径,
AO=
OB
倍,求
a
的度数.
解:在Rt△AOB中,∠
AOB
=90°
A
B
O
当A,B为锐角
时,若A≠B,则
sinA≠sinB,
cosA≠cosB,
tanA≠tanB.
在Rt△ABC中,∠C=90°,
求∠A、∠B的度数.(课本67页第2题)
B
A
C
∴
∠
A=30°
∠B
=
90°-
∠
A
=
90°-30°=
60°
解:在Rt△
ABC中,∠C=90°
巩固训练
1.
cos30°=(
)
2.
计算
2sin45°的结果等于(
)
3.计算:
【解析】
随堂练习
A.
B.
C.
D.
A.
B.
C.
D.
C
A
30°、45°、60°角的正弦值、余弦值和正切值如下表:
对于sinα与tanα,角度越大,函数值也越大;
对于cosα,角度越大,函数值越小。
课堂小结
锐角a
三角函数
30°
45°
60°
sin
a
cos
a
tan
a
课本69页
练习第3题
课堂作业
