人教版数学七年级上册1.4.1有理数的乘法(1)课件(25张PPT)
文档属性
| 名称 | 人教版数学七年级上册1.4.1有理数的乘法(1)课件(25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 574.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-19 00:00:00 | ||
图片预览




文档简介
(共25张PPT)
1.4.1 有理数的乘法
有理数
人教版-数学-七年级上册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-拓展提升
知识回顾
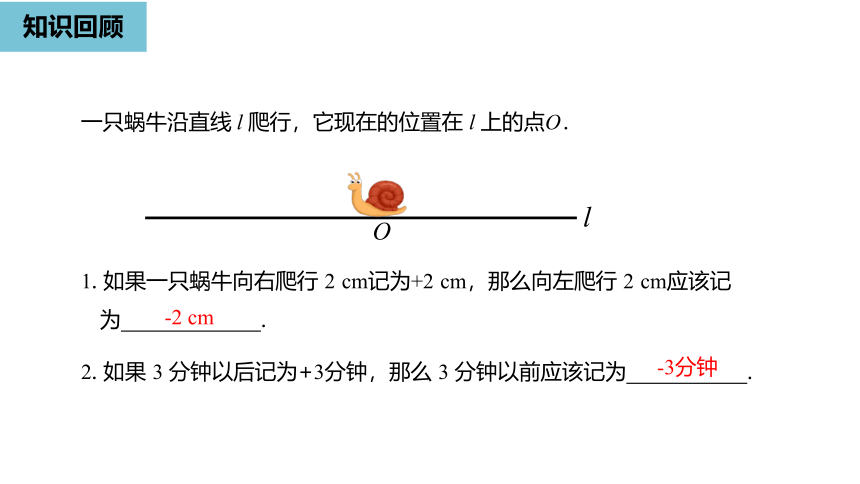
一只蜗牛沿直线
l
爬行,它现在的位置在
l
上的点O.
l
O
1.
如果一只蜗牛向右爬行
2
cm记为+2
cm,那么向左爬行
2
cm应该记为
.
2.
如果
3
分钟以后记为+3分钟,那么
3
分钟以前应该记为
.
-2
cm
-3分钟
学习目标
1.掌握有理数的乘法法则并能熟练运算.
2.掌握多个有理数相乘的积的符号法则.
课堂导入
我们已经熟悉正数及0的乘法运算.与加法类似,引入负数后,将出现
3×(-3),(-3)×3,(-3)×(-3)这样的乘法.该怎样进行这一类的运算呢?
知识点1
新知探究
2
0
2
6
4
l
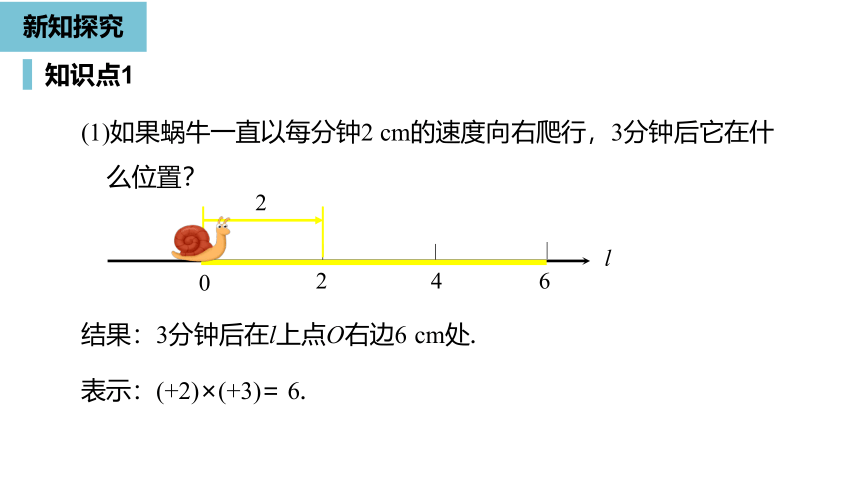
结果:3分钟后在l上点O右边6
cm处.
表示:(+2)×(+3)=
6.
(1)如果蜗牛一直以每分钟2
cm的速度向右爬行,3分钟后它在什么位置?
知识点1
新知探究
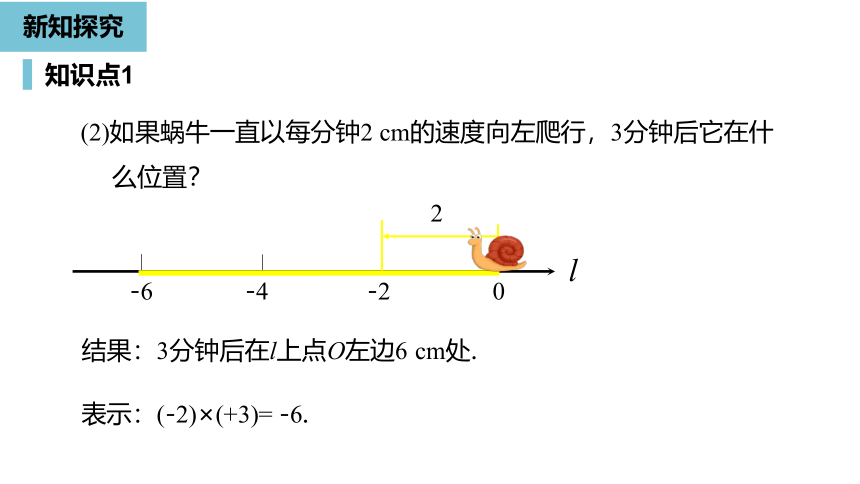
(2)如果蜗牛一直以每分钟2
cm的速度向左爬行,3分钟后它在什么位置?
-6
-4
0
-2
2
l
结果:3分钟后在l上点O左边6
cm处.
表示:(-2)×(+3)=
-6.
知识点1
新知探究
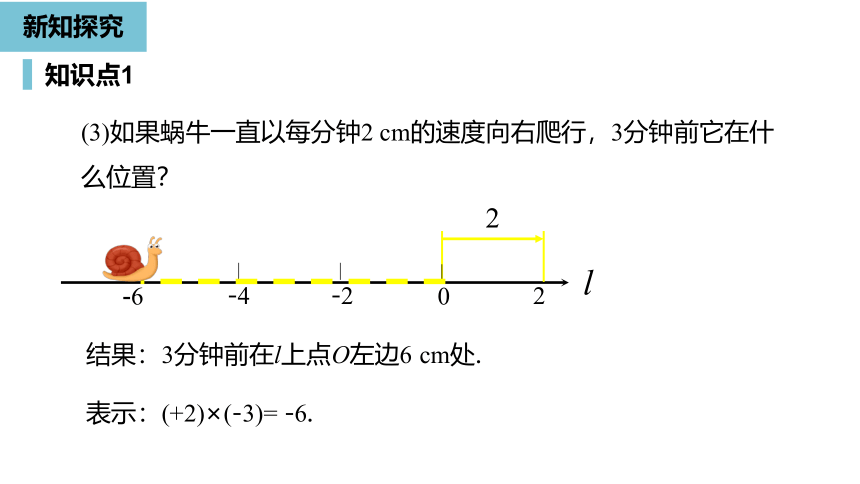
(3)如果蜗牛一直以每分钟2
cm的速度向右爬行,3分钟前它在什么位置?
2
-6
-4
0
-2
2
l
结果:3分钟前在l上点O左边6
cm处.
表示:(+2)×(-3)=
-6.
知识点1
新知探究
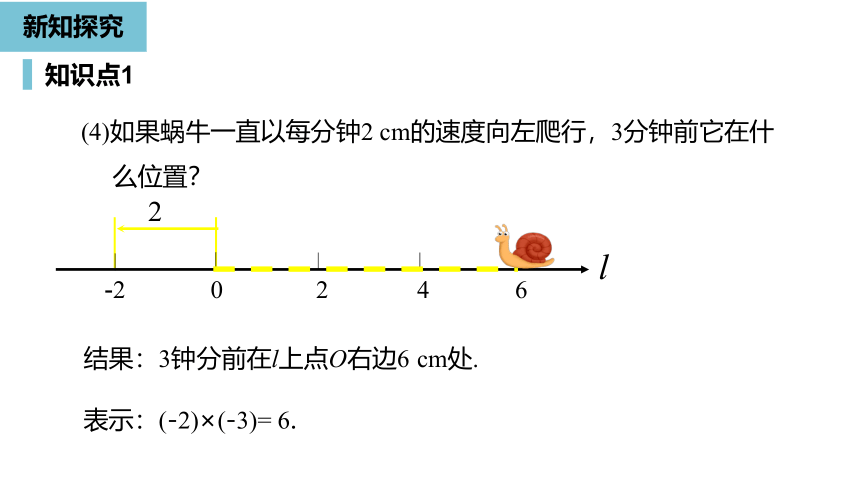
(4)如果蜗牛一直以每分钟2
cm的速度向左爬行,3分钟前它在什么位置?
2
0
2
6
4
-2
l
结果:3钟分前在l上点O右边6
cm处.
表示:(-2)×(-3)=
6.
知识点1
新知探究
结果:都是仍在原处,即结果都是
,
用式子表达:
(5)原地不动或运动了零次,结果是什么?
0×3=0;0×(-3)=0;
2×0=0;(-2)×0=0.
0
O
知识点1
新知探究
1.正数乘正数积为
数;负数乘负数积为
数;
2.负数乘正数积为
数;正数乘负数积为
数;
3.乘积的绝对值等于各乘数绝对值的
;
正
正
负
负
积
(同号得正)
(异号得负)
4.零与任何数相乘或任何数与零相乘结果是
.
零
根据上面结果可知:
(+2)×(+3)=+6
(-2)×(-3)=+6
(-2)×(+3)=-6
(+2)×(-3)=-6
2×0=0
(-2)×0=0
知识点1
新知探究
有理数乘法法则
1.两数相乘,同号得正,异号得负,并把绝对值相乘.
2.任何数同0相乘,都得0.
“同号得正,异号得负”只适用于两个非0的有理数相乘.
知识点1
新知探究
1.两个非0有理数相乘时,先确定积的符号,再确定积的绝对值.
2.两个有理数相乘,当因数中有带分数时,应先把带分数化为假分数再相乘;当因数中既有分数又有小数时,可根据两个数的特点,把分数统一化为小数或把小数统一化为分数再相乘.
3.任何数同1相乘都等于它本身,任何数同-1相乘都等于它的相反数.
知识点1
新知探究
判断下列各式的积是正的还是负的?
2×3×4×(-5)
2×3×(-4)×(-5)
2×(-3)×(-4)×(-5)
(-2)×(-3)×(-4)×(-5)
7.8×(-8.1)×0×(-19.6)
负
正
负
正
零
几个有理数相乘,因数都不为
0
时,积的符号怎样确定?
有一因数为
0
时,积是多少?
知识点1
新知探究
几个不等于零的数相乘,积的符号由_______________决定.
当负因数有_____个时,积为负;
当负因数有_____个时,积为正.
几个数相乘,如果其中有因数为0,_________.
负因数的个数
奇数
偶数
积等于0
}
奇负偶正
跟踪训练
新知探究
计算:
(1)
(-3)×(-4);
(2)
3;
(3)
解:(1)
(-3)×(-4)
=3×4
=12.
(2)
3
=-3
=-
=-12.
(3)=0.
知识点2
新知探究
有理数中,乘积是1的两个数互为倒数.
计算并观察结果有何特点?
(1)
×2; (2)
(-0.25)×(-4).
a≠0
时,a
的倒数是
.
倒数是两个数之间的一种关系,其中一个数叫做另一个数的倒数,单独一个数不能称其为倒数.
知识点2
新知探究
1.求一个不为0的整数的倒数,是用这个数作分母,1作分子的分数,例如:3的倒数是
;
2.求一个真分数的倒数,就是把这个分数的分子和分母交换位置,例如:
-
的倒数是-;
3.求一个带分数的倒数,要先把带分数化成假分数,再交换分子和分母的位置,例如:-,所以-的倒数是;
4.求一个小数的倒数,要先把小数化成分数,再求其倒数,例如:
-0.5=-,所以-0.5的倒数是-2.
求一个数的倒数的方法
知识点2
新知探究
2.倒数等于它本身的数是±1.
1.根据有理数乘法法则中“同号得正”可知:互为倒数的两个数的符号相同,即正数的倒数是正数,负数的倒数是负数,0没有倒数.
跟踪训练
新知探究
求下列各数的倒数.
(1)
-1;
(2)-;
(3)
-1.25;
(4)
2;
(5)
6.5.
解:(1)
-1
的倒数是
-1;
(2)-
的倒数是-;
(3)
-1.25=,所以
-1.25
的倒数是-;
(4)
因为2,所以
的倒数是
;
(5)
因为6.5=,所以
6.5
的倒数是.
随堂练习
1
选择:
(1)
计算
(-1)×(
-2)
的结果是(
)
A.2
B.1
C.
-2
D.
-3
A
(2)
的倒数是(
)
A.2018
B.-2018
C.
D.
A
计算:
(1)
(
-2)×3×4×
(
-5);
(2)
(
-5)
×(-6)
×3×
(
-2);
(3)
(-2016)×(-2017)×2×(-2018)×0×(-2019).
随堂练习
2
解:
(1)
(
-2)×3×4×(-5)
=2×3×4×5
=120.
计算:
(1)
(
-2)×3×4×
(
-5);
(2)
(
-5)
×(-6)
×3×
(
-2);
(3)
(-2016)×(-2017)×2×(-2018)×0×(-2019).
随堂练习
2
解:
(2)
(-5)×(-6)×3×(-2)
=
-5×6×3×2
=
-180.
计算:
(1)
(
-2)×3×4×
(
-5);
(2)
(
-5)
×(-6)
×3×
(
-2);
(3)
(-2016)×(-2017)×2×(-2018)×0×(-2019).
随堂练习
2
解:(3)
(-2016)×(-2017)×2×(
-2018)×0×(
-2019)
=0.
课堂小结
1.有理数乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘.任何数同0相乘,都得0.
2.几个不是零的数相乘,负因数的个数为
奇数时,积为负数.
偶数时,积为正数.
3.几个数相乘,若有因数为零,则积为零.
4.有理数乘法的求解步骤:
有理数相乘,先确定积的符号,再确定积的绝对值.
5.乘积是1的两个数互为倒数.
拓展提升
1
已知有理数
a,b,c,d,m,它们之间有如下关系:a,b互为相反数,c,d
互为倒数,m
的绝对值为
2,则
(a+b+cd
)m-cd
的值是多少?
解:因为
a,b
互为相反数,所以
a+b=0.
因为
c,d
互为倒数,所以
cd=1.
因为
m
的绝对值为
2,所以
m=±2.
当
m=2
时,(a+b+cd)m-cd=(0+1)×2-1=1;
当
m=-2
时,
(a+b+cd)m-cd=(0+1)×(-2)-1=-3.
所以
(a+b+cd)m-cd
的值是
1
或
-3.
1.4.1 有理数的乘法
有理数
人教版-数学-七年级上册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-拓展提升
知识回顾
一只蜗牛沿直线
l
爬行,它现在的位置在
l
上的点O.
l
O
1.
如果一只蜗牛向右爬行
2
cm记为+2
cm,那么向左爬行
2
cm应该记为
.
2.
如果
3
分钟以后记为+3分钟,那么
3
分钟以前应该记为
.
-2
cm
-3分钟
学习目标
1.掌握有理数的乘法法则并能熟练运算.
2.掌握多个有理数相乘的积的符号法则.
课堂导入
我们已经熟悉正数及0的乘法运算.与加法类似,引入负数后,将出现
3×(-3),(-3)×3,(-3)×(-3)这样的乘法.该怎样进行这一类的运算呢?
知识点1
新知探究
2
0
2
6
4
l
结果:3分钟后在l上点O右边6
cm处.
表示:(+2)×(+3)=
6.
(1)如果蜗牛一直以每分钟2
cm的速度向右爬行,3分钟后它在什么位置?
知识点1
新知探究
(2)如果蜗牛一直以每分钟2
cm的速度向左爬行,3分钟后它在什么位置?
-6
-4
0
-2
2
l
结果:3分钟后在l上点O左边6
cm处.
表示:(-2)×(+3)=
-6.
知识点1
新知探究
(3)如果蜗牛一直以每分钟2
cm的速度向右爬行,3分钟前它在什么位置?
2
-6
-4
0
-2
2
l
结果:3分钟前在l上点O左边6
cm处.
表示:(+2)×(-3)=
-6.
知识点1
新知探究
(4)如果蜗牛一直以每分钟2
cm的速度向左爬行,3分钟前它在什么位置?
2
0
2
6
4
-2
l
结果:3钟分前在l上点O右边6
cm处.
表示:(-2)×(-3)=
6.
知识点1
新知探究
结果:都是仍在原处,即结果都是
,
用式子表达:
(5)原地不动或运动了零次,结果是什么?
0×3=0;0×(-3)=0;
2×0=0;(-2)×0=0.
0
O
知识点1
新知探究
1.正数乘正数积为
数;负数乘负数积为
数;
2.负数乘正数积为
数;正数乘负数积为
数;
3.乘积的绝对值等于各乘数绝对值的
;
正
正
负
负
积
(同号得正)
(异号得负)
4.零与任何数相乘或任何数与零相乘结果是
.
零
根据上面结果可知:
(+2)×(+3)=+6
(-2)×(-3)=+6
(-2)×(+3)=-6
(+2)×(-3)=-6
2×0=0
(-2)×0=0
知识点1
新知探究
有理数乘法法则
1.两数相乘,同号得正,异号得负,并把绝对值相乘.
2.任何数同0相乘,都得0.
“同号得正,异号得负”只适用于两个非0的有理数相乘.
知识点1
新知探究
1.两个非0有理数相乘时,先确定积的符号,再确定积的绝对值.
2.两个有理数相乘,当因数中有带分数时,应先把带分数化为假分数再相乘;当因数中既有分数又有小数时,可根据两个数的特点,把分数统一化为小数或把小数统一化为分数再相乘.
3.任何数同1相乘都等于它本身,任何数同-1相乘都等于它的相反数.
知识点1
新知探究
判断下列各式的积是正的还是负的?
2×3×4×(-5)
2×3×(-4)×(-5)
2×(-3)×(-4)×(-5)
(-2)×(-3)×(-4)×(-5)
7.8×(-8.1)×0×(-19.6)
负
正
负
正
零
几个有理数相乘,因数都不为
0
时,积的符号怎样确定?
有一因数为
0
时,积是多少?
知识点1
新知探究
几个不等于零的数相乘,积的符号由_______________决定.
当负因数有_____个时,积为负;
当负因数有_____个时,积为正.
几个数相乘,如果其中有因数为0,_________.
负因数的个数
奇数
偶数
积等于0
}
奇负偶正
跟踪训练
新知探究
计算:
(1)
(-3)×(-4);
(2)
3;
(3)
解:(1)
(-3)×(-4)
=3×4
=12.
(2)
3
=-3
=-
=-12.
(3)=0.
知识点2
新知探究
有理数中,乘积是1的两个数互为倒数.
计算并观察结果有何特点?
(1)
×2; (2)
(-0.25)×(-4).
a≠0
时,a
的倒数是
.
倒数是两个数之间的一种关系,其中一个数叫做另一个数的倒数,单独一个数不能称其为倒数.
知识点2
新知探究
1.求一个不为0的整数的倒数,是用这个数作分母,1作分子的分数,例如:3的倒数是
;
2.求一个真分数的倒数,就是把这个分数的分子和分母交换位置,例如:
-
的倒数是-;
3.求一个带分数的倒数,要先把带分数化成假分数,再交换分子和分母的位置,例如:-,所以-的倒数是;
4.求一个小数的倒数,要先把小数化成分数,再求其倒数,例如:
-0.5=-,所以-0.5的倒数是-2.
求一个数的倒数的方法
知识点2
新知探究
2.倒数等于它本身的数是±1.
1.根据有理数乘法法则中“同号得正”可知:互为倒数的两个数的符号相同,即正数的倒数是正数,负数的倒数是负数,0没有倒数.
跟踪训练
新知探究
求下列各数的倒数.
(1)
-1;
(2)-;
(3)
-1.25;
(4)
2;
(5)
6.5.
解:(1)
-1
的倒数是
-1;
(2)-
的倒数是-;
(3)
-1.25=,所以
-1.25
的倒数是-;
(4)
因为2,所以
的倒数是
;
(5)
因为6.5=,所以
6.5
的倒数是.
随堂练习
1
选择:
(1)
计算
(-1)×(
-2)
的结果是(
)
A.2
B.1
C.
-2
D.
-3
A
(2)
的倒数是(
)
A.2018
B.-2018
C.
D.
A
计算:
(1)
(
-2)×3×4×
(
-5);
(2)
(
-5)
×(-6)
×3×
(
-2);
(3)
(-2016)×(-2017)×2×(-2018)×0×(-2019).
随堂练习
2
解:
(1)
(
-2)×3×4×(-5)
=2×3×4×5
=120.
计算:
(1)
(
-2)×3×4×
(
-5);
(2)
(
-5)
×(-6)
×3×
(
-2);
(3)
(-2016)×(-2017)×2×(-2018)×0×(-2019).
随堂练习
2
解:
(2)
(-5)×(-6)×3×(-2)
=
-5×6×3×2
=
-180.
计算:
(1)
(
-2)×3×4×
(
-5);
(2)
(
-5)
×(-6)
×3×
(
-2);
(3)
(-2016)×(-2017)×2×(-2018)×0×(-2019).
随堂练习
2
解:(3)
(-2016)×(-2017)×2×(
-2018)×0×(
-2019)
=0.
课堂小结
1.有理数乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘.任何数同0相乘,都得0.
2.几个不是零的数相乘,负因数的个数为
奇数时,积为负数.
偶数时,积为正数.
3.几个数相乘,若有因数为零,则积为零.
4.有理数乘法的求解步骤:
有理数相乘,先确定积的符号,再确定积的绝对值.
5.乘积是1的两个数互为倒数.
拓展提升
1
已知有理数
a,b,c,d,m,它们之间有如下关系:a,b互为相反数,c,d
互为倒数,m
的绝对值为
2,则
(a+b+cd
)m-cd
的值是多少?
解:因为
a,b
互为相反数,所以
a+b=0.
因为
c,d
互为倒数,所以
cd=1.
因为
m
的绝对值为
2,所以
m=±2.
当
m=2
时,(a+b+cd)m-cd=(0+1)×2-1=1;
当
m=-2
时,
(a+b+cd)m-cd=(0+1)×(-2)-1=-3.
所以
(a+b+cd)m-cd
的值是
1
或
-3.
