北师大版九年级下册数学 1.1 锐角三角函数(第1课时)课件 (共24张PPT)
文档属性
| 名称 | 北师大版九年级下册数学 1.1 锐角三角函数(第1课时)课件 (共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-20 10:08:27 | ||
图片预览







文档简介
(共24张PPT)
第一章
直角三角形的边角关系
1.1
锐角三角函数(第1课时)
梯子,地面与墙之间就形成一个直角三角形。墙AC和地面BC看成是直角边,梯子AB看成是斜边。
铅直高度
水平宽度
梯子与地面的夹角∠ABC称为倾斜角
从梯子的底端B到墙角C的距离,称为梯子的水平宽度
A
C
B
从梯子的顶端A到墙角C的距离,称为梯子的铅直高度
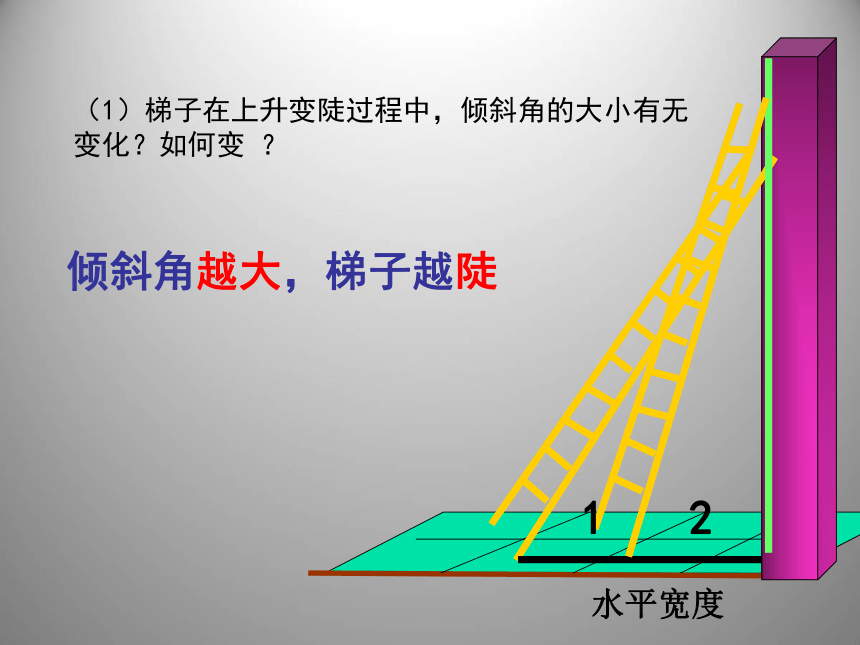
(1)梯子在上升变陡过程中,倾斜角的大小有无变化?如何变
?
水平宽度
1
2
倾斜角越大,梯子越陡
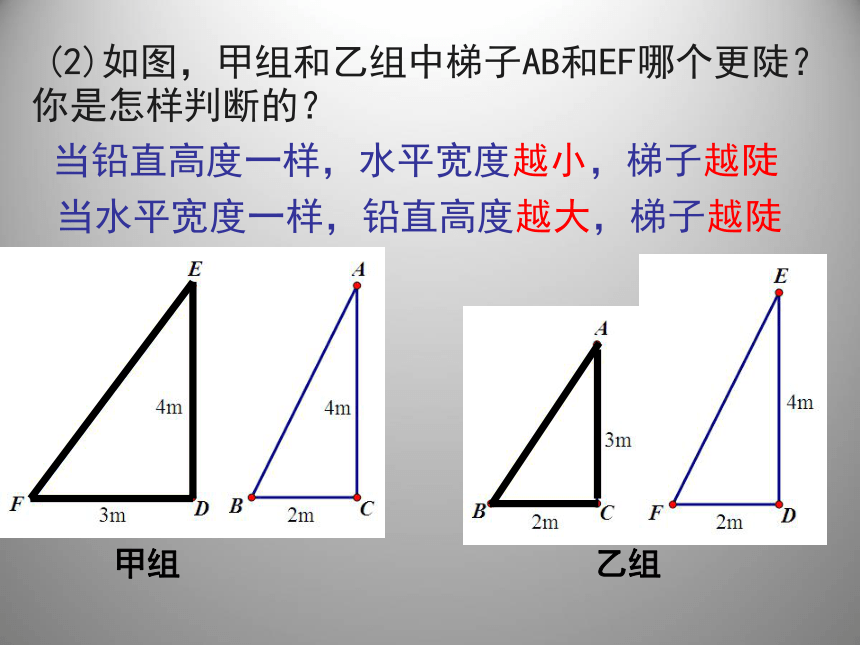
(2)如图,甲组和乙组中梯子AB和EF哪个更陡?
你是怎样判断的?
当铅直高度一样,水平宽度越小,梯子越陡
当水平宽度一样,铅直高度越大,梯子越陡
(3)在下图中,梯子AB和EF哪个更陡?你是怎样判断的?
(4)
右图中哪个梯子更陡?
想一想:如图,小明想通过测量
及
,算出他们的比,来说明梯子的倾斜程度;而小亮则认为,通过测量
及
,算出他们的比,也能说明梯子的倾斜程度你同意小亮的看法吗?
(1)Rt
和
有什么关系?
(2)
和
有什么关系?
(3)若改变
在梯子上的位置?你能得什么结论
相似
相等
正切的定义:
在
Rt△ABC
中,锐角A的对边与邻边的比叫做∠A的正切,记作tanA,即
tanA=
议一议:
梯子的倾斜程度与tanA有什么关系?
tanA的值越大,梯子越陡,∠A越大;
∠A越大,梯子越陡,tanA的值越大。
试一试:
如图,梯子AB和EF哪个更陡?
例1
下图表示两个自动扶梯的几何模型,那一个自动扶梯比较陡?
解:甲梯中
乙梯中
∵
tanα>
tanβ
∴甲梯更陡
请你用不同的符号表示下列图形中两个锐角的正切
定义中应该注意的几个问题:
1、tanA是在直角三角形中定义的,∠A是一个锐角(注意数形结合,构造直角三角形)
2、tanA是一个完整的符号,表示∠A的正切,习惯省去“∠”;
用希腊字母表示角时也可省略;但用三个字母表示角和用阿拉伯数字表示角时,不能省略角的符号“∠”。
3、tanA是一个比值(直角边之比,
注意比的顺序);且tanA﹥0,无单位;
4、tanA的大小只与∠A的大小有关,而与直角三角形的大小无关。
5、两角相等,则其正切值相等;两锐角的正切值相等,则这两个锐角相等。
×
如图
(2)
tanA=
(
)
(3)tanA=
(
)
(4)tanA=0.7m(
)
(5)
tanB=
(
)
×
√
×
×
2、在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,tanA的值(
)
A、扩大100倍
B、缩小100倍
C、不变
D、不能确定
3、已知∠A、∠B为锐角
(1)
若∠A=∠B,则tanA
tanB
(2)若tanA=tanB,则∠A
∠B。
C
=
=
生活中的数学运用
如图:AB称为坡面,
∠
A称为坡角,
注意:坡度也叫坡比,常用i表示
i
=BC/AC
正切经常用来描述山坡的坡度。
坡度(坡比)就是坡面的铅直高度BC与水平宽度AC的比。
坡度是坡角的正切
如图,有一山坡在水平方向上每前进100m,就升高60
m,
那么山坡的坡度(即坡角α的正切——tanα)就是
tanα=
=
1、在右图中
求tanA的值
随堂练习(口答):
2.如图,△ABC是等腰直角三角形,你能根据图中所给数据求出tanC吗?
4、在上图中,若BD=6,CD=12,求tanA的值。
CD
AC
BC
BD
AD
CD
1
2
分析
tanA=tan∠2
=
=
=
5、在梯形ABCD中,AD//BC,AB=DC=13,AD=8,BC=18,求tanB。
E
F
在Rt△ABC中,
如果
锐角A确定,
那么
∠A的对边与邻边的比
随之确定,
这个比叫做
∠A的正切,
记作:tanA
tanA=
∠A的对边
∠A的邻边
∠A的对边
∠A的邻边
tanA越大,梯子越陡,
∠A越大
课堂小结:
坡度(坡比)是坡角的正切。
作业(第4页):
1、在Rt△ABC中,∠C=90°,
AC=5,AB=13,求tanA和tanB.
2
、在Rt△ABC中,∠C=90°,
BC=3,tanA=
,求AC
和AB。
第一章
直角三角形的边角关系
1.1
锐角三角函数(第1课时)
梯子,地面与墙之间就形成一个直角三角形。墙AC和地面BC看成是直角边,梯子AB看成是斜边。
铅直高度
水平宽度
梯子与地面的夹角∠ABC称为倾斜角
从梯子的底端B到墙角C的距离,称为梯子的水平宽度
A
C
B
从梯子的顶端A到墙角C的距离,称为梯子的铅直高度
(1)梯子在上升变陡过程中,倾斜角的大小有无变化?如何变
?
水平宽度
1
2
倾斜角越大,梯子越陡
(2)如图,甲组和乙组中梯子AB和EF哪个更陡?
你是怎样判断的?
当铅直高度一样,水平宽度越小,梯子越陡
当水平宽度一样,铅直高度越大,梯子越陡
(3)在下图中,梯子AB和EF哪个更陡?你是怎样判断的?
(4)
右图中哪个梯子更陡?
想一想:如图,小明想通过测量
及
,算出他们的比,来说明梯子的倾斜程度;而小亮则认为,通过测量
及
,算出他们的比,也能说明梯子的倾斜程度你同意小亮的看法吗?
(1)Rt
和
有什么关系?
(2)
和
有什么关系?
(3)若改变
在梯子上的位置?你能得什么结论
相似
相等
正切的定义:
在
Rt△ABC
中,锐角A的对边与邻边的比叫做∠A的正切,记作tanA,即
tanA=
议一议:
梯子的倾斜程度与tanA有什么关系?
tanA的值越大,梯子越陡,∠A越大;
∠A越大,梯子越陡,tanA的值越大。
试一试:
如图,梯子AB和EF哪个更陡?
例1
下图表示两个自动扶梯的几何模型,那一个自动扶梯比较陡?
解:甲梯中
乙梯中
∵
tanα>
tanβ
∴甲梯更陡
请你用不同的符号表示下列图形中两个锐角的正切
定义中应该注意的几个问题:
1、tanA是在直角三角形中定义的,∠A是一个锐角(注意数形结合,构造直角三角形)
2、tanA是一个完整的符号,表示∠A的正切,习惯省去“∠”;
用希腊字母表示角时也可省略;但用三个字母表示角和用阿拉伯数字表示角时,不能省略角的符号“∠”。
3、tanA是一个比值(直角边之比,
注意比的顺序);且tanA﹥0,无单位;
4、tanA的大小只与∠A的大小有关,而与直角三角形的大小无关。
5、两角相等,则其正切值相等;两锐角的正切值相等,则这两个锐角相等。
×
如图
(2)
tanA=
(
)
(3)tanA=
(
)
(4)tanA=0.7m(
)
(5)
tanB=
(
)
×
√
×
×
2、在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,tanA的值(
)
A、扩大100倍
B、缩小100倍
C、不变
D、不能确定
3、已知∠A、∠B为锐角
(1)
若∠A=∠B,则tanA
tanB
(2)若tanA=tanB,则∠A
∠B。
C
=
=
生活中的数学运用
如图:AB称为坡面,
∠
A称为坡角,
注意:坡度也叫坡比,常用i表示
i
=BC/AC
正切经常用来描述山坡的坡度。
坡度(坡比)就是坡面的铅直高度BC与水平宽度AC的比。
坡度是坡角的正切
如图,有一山坡在水平方向上每前进100m,就升高60
m,
那么山坡的坡度(即坡角α的正切——tanα)就是
tanα=
=
1、在右图中
求tanA的值
随堂练习(口答):
2.如图,△ABC是等腰直角三角形,你能根据图中所给数据求出tanC吗?
4、在上图中,若BD=6,CD=12,求tanA的值。
CD
AC
BC
BD
AD
CD
1
2
分析
tanA=tan∠2
=
=
=
5、在梯形ABCD中,AD//BC,AB=DC=13,AD=8,BC=18,求tanB。
E
F
在Rt△ABC中,
如果
锐角A确定,
那么
∠A的对边与邻边的比
随之确定,
这个比叫做
∠A的正切,
记作:tanA
tanA=
∠A的对边
∠A的邻边
∠A的对边
∠A的邻边
tanA越大,梯子越陡,
∠A越大
课堂小结:
坡度(坡比)是坡角的正切。
作业(第4页):
1、在Rt△ABC中,∠C=90°,
AC=5,AB=13,求tanA和tanB.
2
、在Rt△ABC中,∠C=90°,
BC=3,tanA=
,求AC
和AB。
