人教版数学七年级上册1.2.4绝对值课件(21张PPT)
文档属性
| 名称 | 人教版数学七年级上册1.2.4绝对值课件(21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 329.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-19 22:09:51 | ||
图片预览







文档简介
(共21张PPT)
1.2.4绝对值
有理数
人教版-数学-七年级上册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-拓展提升
知识回顾
1.什么是数轴?
数轴是规定了原点、正方向、单位长度的直线.
2.什么是相反数?
只有符号不同的两个数叫做互为相反数.
规定:0的相反数是0.
学习目标
1.理解绝对值的概念及性质.
3.通过探究得出有理数大小的比较方法.
4.能利用数轴及绝对值的知识,比较两个有理数的大小.
2.会求一个有理数的绝对值.
课堂导入
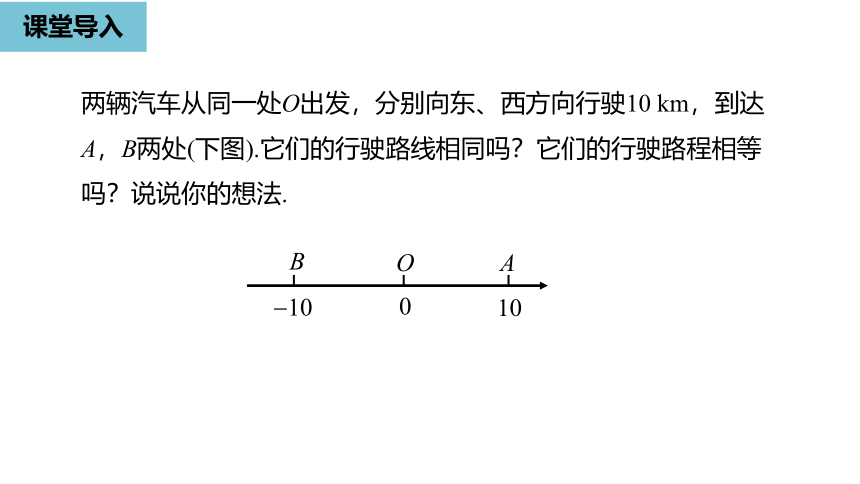
两辆汽车从同一处O出发,分别向东、西方向行驶10
km,到达A,B两处(下图).它们的行驶路线相同吗?它们的行驶路程相等吗?说说你的想法.
-10
10
0
B
A
O
知识点1
新知探究
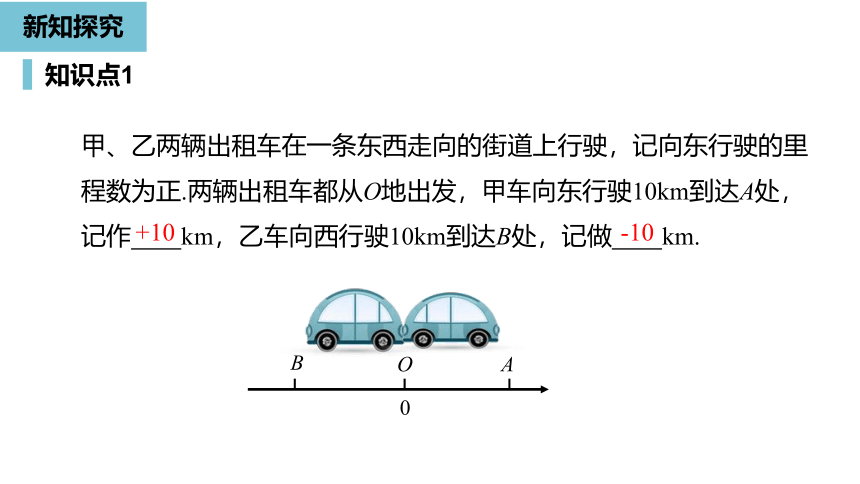
甲、乙两辆出租车在一条东西走向的街道上行驶,记向东行驶的里程数为正.两辆出租车都从O地出发,甲车向东行驶10km到达A处,记作
km,乙车向西行驶10km到达B处,记做
km.
+10
-10
0
O
B
A
知识点1
新知探究
一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值,记作|a|
.
(这里的数a可以是正数、负数和0).
任何数都有绝对值,并且只有一个,数a的绝对值,是表示它的点到原点的距离.因为距离不可能是负数,所以数a的绝对值|a|为非负数,即|a|≥0.
知识点1
新知探究
|5|=5
|-10|=10
|3.5|=
3.5
|100|=100
|-3|=3
|50|=50
|-4.5|=4.5
|-5000|=5000
|0|=0
…..
一个正数的绝对值是什么?
一个负数的绝对值是什么?
0的绝对值是什么?
观察这些表示绝对值的数,它们有什么共同点?
绝对值的性质
一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对
值是0.即
(1)
如果a>0,那么|a|=a;
(2)
如果a=0,那么|a|=0;
(3)
如果a<0,那么|a|=-a.
知识点1
新知探究
(1)
任何数的绝对值都不小于它本身,即|a|≥a.
(2)若几个数的绝对值之和为0,则这个算式中的每个数都为0,即若|a|
+
|b|
+...+
|m|=0,则a=b=…=m
=0.
知识点1
新知探究
活学巧记
绝对值,总非负,
它的符号是两竖.
正数和0取绝对值,
结果都是它本身.
负数若取绝对值,
结果是其相反数.
知识点1
新知探究
(1)
在数轴上,表示一个数的点离原点越近,这个数的绝对值越小;离原点越远,这个数的绝对值越大.
(2)
绝对值是它本身的数是非负数,即若|a|
=a,则a≥0;绝对值是其相反数的数是非正数,即若|a|=-a,则a≤0.
(3)绝对值是某个正数的数有两个,它们互为相反数,即若|x|
=a
(a>0),则x=±a,如|x|=2,则x=±2.
(4)
互为相反数的两个数的绝对值相等,即若a=-b,则|a|=|b|;绝对值相等的两个数相等或互为相反数,即若|a|=|b|,则a=b或a=-b.
跟踪训练
新知探究
计算:
(1)
|-19|-|10|;(2)
-|8-6|;(3)
;(4)
|-2|×||.
解:(1)
|-19|-|10|=19-10=9.
(2)
-|8-6|=-|2|=-2.
(3)
.
(4)
|-2|×||=2×=3.
知识点2
新知探究
下面是某一天我国5个城市的最低气温.
武汉5
℃
北京-10℃ 上海0℃
广州10℃
哈尔滨-20℃
你能将上述五个城市的最低气温按从低到高的顺序依次排列吗?
哈尔滨
-20℃
北京
-10℃
上海
0℃
武汉
5℃
广州
10℃
<
<
<
<
知识点2
新知探究
这五个数的大小与它们在数轴上的位置有什么关系?
越
来
越
大
-20
-10
0
5
10
●
●
●
●
●
哈尔滨
-20℃
北京
-10℃
上海
0℃
武汉
5℃
广州
10℃
<
<
<
<
知识点2
新知探究
有理数大小的比较方法1:
数轴比较法:
在数轴上表示的两个数,右边的数总比左边的数大.
-5
-4
-3
-2
-1
0
1
2
3
4
5
小
大
知识点2
新知探究
对于正数、0、负数这三类数,它们之间有什么大小关系?两个负数之间如何比较大小?
根据法则比较有理数的大小:
(1)正数大于0,0大于负数,正数大于负数;
(2)两个负数,绝对值大的反而小.
知识点2
新知探究
利用法则比较两个数的大小时,可按数的性质符号分类.具体如下:
两数同号
同为正号,绝对值大的数大
同为负号,绝对值大的反而小
两数异号
正数大于负数
一数为0
正数与0,正数大于0
负数与0,负数小于0
跟踪训练
新知探究
比较下列各对数的大小:
(1)
3和-5;
(2)
-3和-5.
解:(1)
3>-5;
(2)
-3>-5.
随堂练习
1
如果a=-4,且|a|=|b|,求|b+4|的值.
解:因为a=-4,所以|b|=|a|=|-4|=4.
所以b=4或b=-4.
当b=4时,|b+4|=|4+4|=8;
当b=-4时,|b+4|=|-4+4|=0.
所以|b+4|的值是8或0.
随堂练习
2
把有理数
-1,1,0,-3,-5,3
按从小到大的顺序用“<”号连接起来.
解:-5<
-3<-1<0<1<3.
课堂小结
3.比较有理数大小的方法
方法①:数轴上表示的两个数,右边的总比左边的大.
方法②:正数大于0,0大于负数,正数大于负数;两个负数,绝对值大的反而小.
1.数轴上表示数a的点与原点的距离叫做数a的绝对值.
2.绝对值的性质
(1)|a|≥0;
(2)
拓展提升
1
若|a-1|+|b-2|=0,求a+b的值.
解:因为|a-1|+|b-2|=0,且|a-1|≥0,|b-2|≥0,
所以|a-1|=0,|b-2|=0.
所以a-1=0,b-
2=0,即a=1,b=2.
所以a+b=1+2=3.
利用绝对值的非负性求值
绝对值的定义揭示了绝对值的一个重要性质:非负性,即对任意有理数a,|a|≥0.若几个非负数的和为0,则这些非负数均为0.
1.2.4绝对值
有理数
人教版-数学-七年级上册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-拓展提升
知识回顾
1.什么是数轴?
数轴是规定了原点、正方向、单位长度的直线.
2.什么是相反数?
只有符号不同的两个数叫做互为相反数.
规定:0的相反数是0.
学习目标
1.理解绝对值的概念及性质.
3.通过探究得出有理数大小的比较方法.
4.能利用数轴及绝对值的知识,比较两个有理数的大小.
2.会求一个有理数的绝对值.
课堂导入
两辆汽车从同一处O出发,分别向东、西方向行驶10
km,到达A,B两处(下图).它们的行驶路线相同吗?它们的行驶路程相等吗?说说你的想法.
-10
10
0
B
A
O
知识点1
新知探究
甲、乙两辆出租车在一条东西走向的街道上行驶,记向东行驶的里程数为正.两辆出租车都从O地出发,甲车向东行驶10km到达A处,记作
km,乙车向西行驶10km到达B处,记做
km.
+10
-10
0
O
B
A
知识点1
新知探究
一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值,记作|a|
.
(这里的数a可以是正数、负数和0).
任何数都有绝对值,并且只有一个,数a的绝对值,是表示它的点到原点的距离.因为距离不可能是负数,所以数a的绝对值|a|为非负数,即|a|≥0.
知识点1
新知探究
|5|=5
|-10|=10
|3.5|=
3.5
|100|=100
|-3|=3
|50|=50
|-4.5|=4.5
|-5000|=5000
|0|=0
…..
一个正数的绝对值是什么?
一个负数的绝对值是什么?
0的绝对值是什么?
观察这些表示绝对值的数,它们有什么共同点?
绝对值的性质
一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对
值是0.即
(1)
如果a>0,那么|a|=a;
(2)
如果a=0,那么|a|=0;
(3)
如果a<0,那么|a|=-a.
知识点1
新知探究
(1)
任何数的绝对值都不小于它本身,即|a|≥a.
(2)若几个数的绝对值之和为0,则这个算式中的每个数都为0,即若|a|
+
|b|
+...+
|m|=0,则a=b=…=m
=0.
知识点1
新知探究
活学巧记
绝对值,总非负,
它的符号是两竖.
正数和0取绝对值,
结果都是它本身.
负数若取绝对值,
结果是其相反数.
知识点1
新知探究
(1)
在数轴上,表示一个数的点离原点越近,这个数的绝对值越小;离原点越远,这个数的绝对值越大.
(2)
绝对值是它本身的数是非负数,即若|a|
=a,则a≥0;绝对值是其相反数的数是非正数,即若|a|=-a,则a≤0.
(3)绝对值是某个正数的数有两个,它们互为相反数,即若|x|
=a
(a>0),则x=±a,如|x|=2,则x=±2.
(4)
互为相反数的两个数的绝对值相等,即若a=-b,则|a|=|b|;绝对值相等的两个数相等或互为相反数,即若|a|=|b|,则a=b或a=-b.
跟踪训练
新知探究
计算:
(1)
|-19|-|10|;(2)
-|8-6|;(3)
;(4)
|-2|×||.
解:(1)
|-19|-|10|=19-10=9.
(2)
-|8-6|=-|2|=-2.
(3)
.
(4)
|-2|×||=2×=3.
知识点2
新知探究
下面是某一天我国5个城市的最低气温.
武汉5
℃
北京-10℃ 上海0℃
广州10℃
哈尔滨-20℃
你能将上述五个城市的最低气温按从低到高的顺序依次排列吗?
哈尔滨
-20℃
北京
-10℃
上海
0℃
武汉
5℃
广州
10℃
<
<
<
<
知识点2
新知探究
这五个数的大小与它们在数轴上的位置有什么关系?
越
来
越
大
-20
-10
0
5
10
●
●
●
●
●
哈尔滨
-20℃
北京
-10℃
上海
0℃
武汉
5℃
广州
10℃
<
<
<
<
知识点2
新知探究
有理数大小的比较方法1:
数轴比较法:
在数轴上表示的两个数,右边的数总比左边的数大.
-5
-4
-3
-2
-1
0
1
2
3
4
5
小
大
知识点2
新知探究
对于正数、0、负数这三类数,它们之间有什么大小关系?两个负数之间如何比较大小?
根据法则比较有理数的大小:
(1)正数大于0,0大于负数,正数大于负数;
(2)两个负数,绝对值大的反而小.
知识点2
新知探究
利用法则比较两个数的大小时,可按数的性质符号分类.具体如下:
两数同号
同为正号,绝对值大的数大
同为负号,绝对值大的反而小
两数异号
正数大于负数
一数为0
正数与0,正数大于0
负数与0,负数小于0
跟踪训练
新知探究
比较下列各对数的大小:
(1)
3和-5;
(2)
-3和-5.
解:(1)
3>-5;
(2)
-3>-5.
随堂练习
1
如果a=-4,且|a|=|b|,求|b+4|的值.
解:因为a=-4,所以|b|=|a|=|-4|=4.
所以b=4或b=-4.
当b=4时,|b+4|=|4+4|=8;
当b=-4时,|b+4|=|-4+4|=0.
所以|b+4|的值是8或0.
随堂练习
2
把有理数
-1,1,0,-3,-5,3
按从小到大的顺序用“<”号连接起来.
解:-5<
-3<-1<0<1<3.
课堂小结
3.比较有理数大小的方法
方法①:数轴上表示的两个数,右边的总比左边的大.
方法②:正数大于0,0大于负数,正数大于负数;两个负数,绝对值大的反而小.
1.数轴上表示数a的点与原点的距离叫做数a的绝对值.
2.绝对值的性质
(1)|a|≥0;
(2)
拓展提升
1
若|a-1|+|b-2|=0,求a+b的值.
解:因为|a-1|+|b-2|=0,且|a-1|≥0,|b-2|≥0,
所以|a-1|=0,|b-2|=0.
所以a-1=0,b-
2=0,即a=1,b=2.
所以a+b=1+2=3.
利用绝对值的非负性求值
绝对值的定义揭示了绝对值的一个重要性质:非负性,即对任意有理数a,|a|≥0.若几个非负数的和为0,则这些非负数均为0.
