人教版数学七年级上册1.3.1有理数的加法(2)课件(22张PPT)
文档属性
| 名称 | 人教版数学七年级上册1.3.1有理数的加法(2)课件(22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 370.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-19 22:11:33 | ||
图片预览








文档简介
(共22张PPT)
1.3.1 有理数的加法
有理数
人教版-数学-七年级上册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-拓展提升
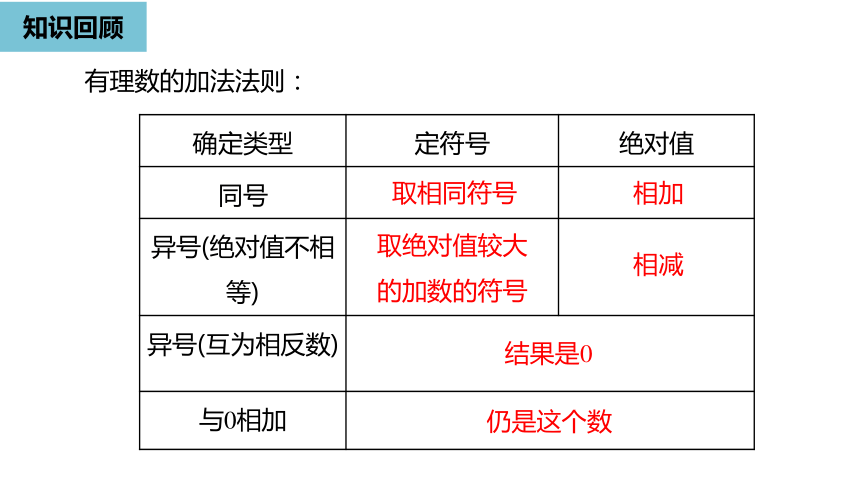
知识回顾
确定类型
定符号
绝对值
同号
异号(绝对值不相等)
异号(互为相反数)
与0相加
取相同符号
取绝对值较大的加数的符号
相加
相减
结果是0
仍是这个数
有理数的加法法则:
学习目标
1.能概括出有理数的加法交换律和结合律.
2.灵活熟练地运用加法交换律、结合律简化运算.
课堂导入
为了防止水土流失,保护环境,某县从
2013
年起开始实施植树造林,其中
2013
年完成
786
亩,2014
年完成
957
亩,2015
年完成
1
214
亩,2016
年完成
1
543
亩.该县从
2013
年到
2016
年一共完成植树造林多少亩?看谁算得又对又快!
知识点1
新知探究
-2
-2
填一填:(1)
3+(-5)=
;
(-5)+3=
.
(2)
13+(-9)=
;
(-9)+13=
.
4
4
(1)比较以上各组两个算式的结果,每组两个算式有什么特征?
(2)小学学的加法交换律在有理数的加法中还适用吗?
知识点1
新知探究
a+b=b+a.
加法结合律:
用字母表示为:
在有理数加法中,两个数相加,交换加数的位置,和不变.
填一填:(1)
[3+(-5)]-(-7)=
;
3+[(-5)-(-7)]=
.
(2)
[8+(-4)]+(-6)=
;
8+[(-4)+(-6)]=
.
知识点1
新知探究
5
5
-2
-2
(1)比较以上各组两个算式的结果,每组两个算式有什么特征?
(2)小学学的加法结合律在有理数的加法中还适用吗?
知识点1
新知探究
(a+b)+c=a+(b+c).
加法结合律:
用字母表示为:
在有理数的加法中,三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.
知识点1
新知探究
例
计算16+(-25)+24+(-35).
解:
16+(-25)+24+(-35)
=16+24+[(-25)+
(-35)]
=40+(-60)
=-20.
“同号结合法”进行有理数的加法运算
在多个有理数相加时,若既有正数又有负数,可将所有的正数结合在一起,所有的负数结合在一起,分别相加,再进行计算.这种方法可减少异号两数相加的次数,达到简化运算的目的.
知识点1
新知探究
1.有理数的加法运算律不但适用于两个数或三个数相加,而且适用于三个以
上有理数相加.
2.利用有理数的加法交换律时,要适当加括号,如-6.6+2+(-3.4)=2+(
-6.6)
+(
-3.4).
3.灵活运用加法运算律,能使运算过程简化,通常有以下规律:
①互为相反数的两数先相加;
②符号相同的数先相加;
③分母相同的数先相加;
④相加能得到整数的数先相加;
⑤带分数相加时,先拆成整数和分数,再利用加法运算律相加.
知识点1
新知探究
例
每袋小麦的标准重量为
90
千克,10
袋小麦称重记录如图所示,与标准重量比较,10
袋小麦总计超过多少千克或不足多少千克?10
袋小麦的总重量是多少?
91
91
91.3
88.7
91.5
89
91.2
88.8
91.8
91.1
知识点1
新知探究
解法1:先计算10袋小麦的总重量:
91+91+91.5+89+91.2+91.3+88.7+88.8+91.8+91.1=905.4;
再计算总计超过多少千克:
905.4-90×10=5.4.
答:10袋小麦总计超过标准重量5.4千克,总重量是905.4千克.
91
91
91.3
88.7
91.5
89
91.2
88.8
91.8
91.1
知识点1
新知探究
解法2:每袋小麦超过标准重量的千克数记作正数,不足的千克数记作负
数,10袋小麦对应的数为+1,+1,+1.5,-1,+1.2,+1.3,-1.3,
-1.2,+1.8,+1.1.
1+1+1.5+(-1)+1.2+1.3+(-1.3)+(-1.2)+1.8+1.1
=[1+(-1)]+[1.2+(-1.2)]+[1.3+(-1.3)]+(1+1.5+1.8+1.1)
=5.4.
90×10+5.4=905.4.
答:10袋小麦总计超过标准重量5.4千克,总重量是905.4千克.
91
91
91.3
88.7
91.5
89
91.2
88.8
91.8
91.1
跟踪训练
新知探究
计算:.
解:
=
=
=.
随堂练习
1
计算:
(1)
23+(-17)+6+(-22);
=(23+6)+[(-27)+(-22)]
=29-49
=-20.
=(3+1+2)+[(-2)+(-3)+(-4)]
=6-9
=-3.
(2)
(-2)+3+1+(-3)+2+(-4).
解:(1)
23+(-17)+6+(-22)
(2)
(-2)+3+1+(-3)+2+(-4)
随堂练习
2
计算:25.3+(-7.3)+(-13.7)+7.7.
解:
25.3+(-7.3)+(-13.7)+7.7
=(25.3+7.7)+[(-7.3)+(-13.7)]
=33+(-21)
=12.
凑整法
多个有理数相加时,如果既有分数,也有小数,一般将存在数量少的形式转化成数量多的形式,把能凑成整数的数结合在一起,可以使计算简便,这种方法简称“凑整法".
随堂练习
3
计算:.
解:
=
=
=
=.
课堂小结
加法运算律
加法的交换律:a+b=b+a.
加法的结合律:
a+b+c=a+(b+c)=a+(b+c)
.
简化运算
拓展提升
1
计算:(-3)+4+(+2)+(-6)+7+(-5).
解:
(-3)+4+(+2)+(-6)+7+(-5)
=
(-3)+(-6)+(-5)+4+(+2)+7
=
[(-3)+(-6)+(-5)]+[4+(+2)+7]
=
(-14)+13
=
-1.
拓展提升
2
计算:.
解:
=
=
=.
拓展提升
3
为了有效防止酒后驾车,某市一辆交通巡逻车在一条东西方向的公路上巡逻.如果规定向东为正,向西为负,那么该汽车从出发点开始行驶的路程为:+2,-3,+2,+1,-2,-1,-2
(单位:千米).
(1)
此时,这辆交通巡逻车的司机该如何向队长描述他的位置?
(2)
如果队长命令他马上返回出发点,那么这次巡逻(含返回)共耗油多少升?(已知这辆交通巡逻车每千米耗油
0.2
升)
解:(1)
(+2)+(-3)+(+2)+(+1)+(-2)+(-1)+(-2)=-3,
所以此时这辆交通巡逻车位于出发点正西方向
3
千米处.
拓展提升
3
解:(2)
这辆交通巡逻车行驶的总路程(含返回)为:
|+2|+|-3|+|+2|+|+1|+|-2|+|-1|+|-2|+3=16
(千米).
16×0.2=3.2
(升).
答:这次巡逻共耗油
3.2
升.
为了有效防止酒后驾车,某市一辆交通巡逻车在一条东西方向的公路上巡逻.如果规定向东为正,向西为负,那么该汽车从出发点开始行驶的过程为:+2,-3,+2,+1,-2,-1,-2
(单位:千米).
(1)
此时,这辆交通巡逻车的司机该如何向队长描述他的位置?
(2)
如果队长命令他马上返回出发点,那么这次巡逻(含返回)共耗油多少升?(已知这辆交通巡逻车每千米耗油
0.2
升)
1.3.1 有理数的加法
有理数
人教版-数学-七年级上册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-拓展提升
知识回顾
确定类型
定符号
绝对值
同号
异号(绝对值不相等)
异号(互为相反数)
与0相加
取相同符号
取绝对值较大的加数的符号
相加
相减
结果是0
仍是这个数
有理数的加法法则:
学习目标
1.能概括出有理数的加法交换律和结合律.
2.灵活熟练地运用加法交换律、结合律简化运算.
课堂导入
为了防止水土流失,保护环境,某县从
2013
年起开始实施植树造林,其中
2013
年完成
786
亩,2014
年完成
957
亩,2015
年完成
1
214
亩,2016
年完成
1
543
亩.该县从
2013
年到
2016
年一共完成植树造林多少亩?看谁算得又对又快!
知识点1
新知探究
-2
-2
填一填:(1)
3+(-5)=
;
(-5)+3=
.
(2)
13+(-9)=
;
(-9)+13=
.
4
4
(1)比较以上各组两个算式的结果,每组两个算式有什么特征?
(2)小学学的加法交换律在有理数的加法中还适用吗?
知识点1
新知探究
a+b=b+a.
加法结合律:
用字母表示为:
在有理数加法中,两个数相加,交换加数的位置,和不变.
填一填:(1)
[3+(-5)]-(-7)=
;
3+[(-5)-(-7)]=
.
(2)
[8+(-4)]+(-6)=
;
8+[(-4)+(-6)]=
.
知识点1
新知探究
5
5
-2
-2
(1)比较以上各组两个算式的结果,每组两个算式有什么特征?
(2)小学学的加法结合律在有理数的加法中还适用吗?
知识点1
新知探究
(a+b)+c=a+(b+c).
加法结合律:
用字母表示为:
在有理数的加法中,三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.
知识点1
新知探究
例
计算16+(-25)+24+(-35).
解:
16+(-25)+24+(-35)
=16+24+[(-25)+
(-35)]
=40+(-60)
=-20.
“同号结合法”进行有理数的加法运算
在多个有理数相加时,若既有正数又有负数,可将所有的正数结合在一起,所有的负数结合在一起,分别相加,再进行计算.这种方法可减少异号两数相加的次数,达到简化运算的目的.
知识点1
新知探究
1.有理数的加法运算律不但适用于两个数或三个数相加,而且适用于三个以
上有理数相加.
2.利用有理数的加法交换律时,要适当加括号,如-6.6+2+(-3.4)=2+(
-6.6)
+(
-3.4).
3.灵活运用加法运算律,能使运算过程简化,通常有以下规律:
①互为相反数的两数先相加;
②符号相同的数先相加;
③分母相同的数先相加;
④相加能得到整数的数先相加;
⑤带分数相加时,先拆成整数和分数,再利用加法运算律相加.
知识点1
新知探究
例
每袋小麦的标准重量为
90
千克,10
袋小麦称重记录如图所示,与标准重量比较,10
袋小麦总计超过多少千克或不足多少千克?10
袋小麦的总重量是多少?
91
91
91.3
88.7
91.5
89
91.2
88.8
91.8
91.1
知识点1
新知探究
解法1:先计算10袋小麦的总重量:
91+91+91.5+89+91.2+91.3+88.7+88.8+91.8+91.1=905.4;
再计算总计超过多少千克:
905.4-90×10=5.4.
答:10袋小麦总计超过标准重量5.4千克,总重量是905.4千克.
91
91
91.3
88.7
91.5
89
91.2
88.8
91.8
91.1
知识点1
新知探究
解法2:每袋小麦超过标准重量的千克数记作正数,不足的千克数记作负
数,10袋小麦对应的数为+1,+1,+1.5,-1,+1.2,+1.3,-1.3,
-1.2,+1.8,+1.1.
1+1+1.5+(-1)+1.2+1.3+(-1.3)+(-1.2)+1.8+1.1
=[1+(-1)]+[1.2+(-1.2)]+[1.3+(-1.3)]+(1+1.5+1.8+1.1)
=5.4.
90×10+5.4=905.4.
答:10袋小麦总计超过标准重量5.4千克,总重量是905.4千克.
91
91
91.3
88.7
91.5
89
91.2
88.8
91.8
91.1
跟踪训练
新知探究
计算:.
解:
=
=
=.
随堂练习
1
计算:
(1)
23+(-17)+6+(-22);
=(23+6)+[(-27)+(-22)]
=29-49
=-20.
=(3+1+2)+[(-2)+(-3)+(-4)]
=6-9
=-3.
(2)
(-2)+3+1+(-3)+2+(-4).
解:(1)
23+(-17)+6+(-22)
(2)
(-2)+3+1+(-3)+2+(-4)
随堂练习
2
计算:25.3+(-7.3)+(-13.7)+7.7.
解:
25.3+(-7.3)+(-13.7)+7.7
=(25.3+7.7)+[(-7.3)+(-13.7)]
=33+(-21)
=12.
凑整法
多个有理数相加时,如果既有分数,也有小数,一般将存在数量少的形式转化成数量多的形式,把能凑成整数的数结合在一起,可以使计算简便,这种方法简称“凑整法".
随堂练习
3
计算:.
解:
=
=
=
=.
课堂小结
加法运算律
加法的交换律:a+b=b+a.
加法的结合律:
a+b+c=a+(b+c)=a+(b+c)
.
简化运算
拓展提升
1
计算:(-3)+4+(+2)+(-6)+7+(-5).
解:
(-3)+4+(+2)+(-6)+7+(-5)
=
(-3)+(-6)+(-5)+4+(+2)+7
=
[(-3)+(-6)+(-5)]+[4+(+2)+7]
=
(-14)+13
=
-1.
拓展提升
2
计算:.
解:
=
=
=.
拓展提升
3
为了有效防止酒后驾车,某市一辆交通巡逻车在一条东西方向的公路上巡逻.如果规定向东为正,向西为负,那么该汽车从出发点开始行驶的路程为:+2,-3,+2,+1,-2,-1,-2
(单位:千米).
(1)
此时,这辆交通巡逻车的司机该如何向队长描述他的位置?
(2)
如果队长命令他马上返回出发点,那么这次巡逻(含返回)共耗油多少升?(已知这辆交通巡逻车每千米耗油
0.2
升)
解:(1)
(+2)+(-3)+(+2)+(+1)+(-2)+(-1)+(-2)=-3,
所以此时这辆交通巡逻车位于出发点正西方向
3
千米处.
拓展提升
3
解:(2)
这辆交通巡逻车行驶的总路程(含返回)为:
|+2|+|-3|+|+2|+|+1|+|-2|+|-1|+|-2|+3=16
(千米).
16×0.2=3.2
(升).
答:这次巡逻共耗油
3.2
升.
为了有效防止酒后驾车,某市一辆交通巡逻车在一条东西方向的公路上巡逻.如果规定向东为正,向西为负,那么该汽车从出发点开始行驶的过程为:+2,-3,+2,+1,-2,-1,-2
(单位:千米).
(1)
此时,这辆交通巡逻车的司机该如何向队长描述他的位置?
(2)
如果队长命令他马上返回出发点,那么这次巡逻(含返回)共耗油多少升?(已知这辆交通巡逻车每千米耗油
0.2
升)
