人教版数学七年级上册1.3.2有理数的减法(1)课件(17张PPT)
文档属性
| 名称 | 人教版数学七年级上册1.3.2有理数的减法(1)课件(17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 123.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-19 22:12:29 | ||
图片预览





文档简介
(共17张PPT)
1.3.2 有理数的减法
有理数
人教版-数学-七年级上册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-拓展提升
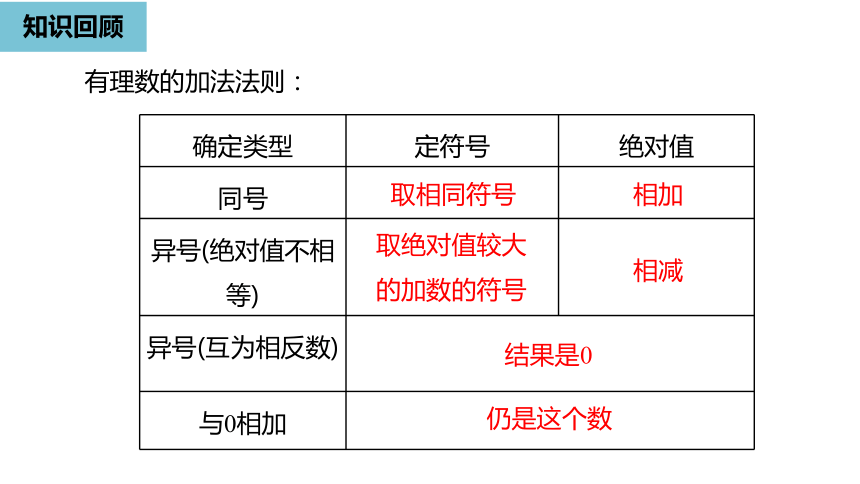
知识回顾
确定类型
定符号
绝对值
同号
异号(绝对值不相等)
异号(互为相反数)
与0相加
取相同符号
取绝对值较大的加数的符号
相加
相减
结果是0
仍是这个数
有理数的加法法则:
学习目标
1.理解、掌握有理数的减法法则,会将有理数的减法运算转化为加法运算.
2.通过把有理数的减法运算转化为加法运算,渗透转化思想,培养运算能力.
课堂导入
北京某天气温是-3?C~3?C,你能列式表示这天的温差是多少摄氏度吗?
知识点1
新知探究
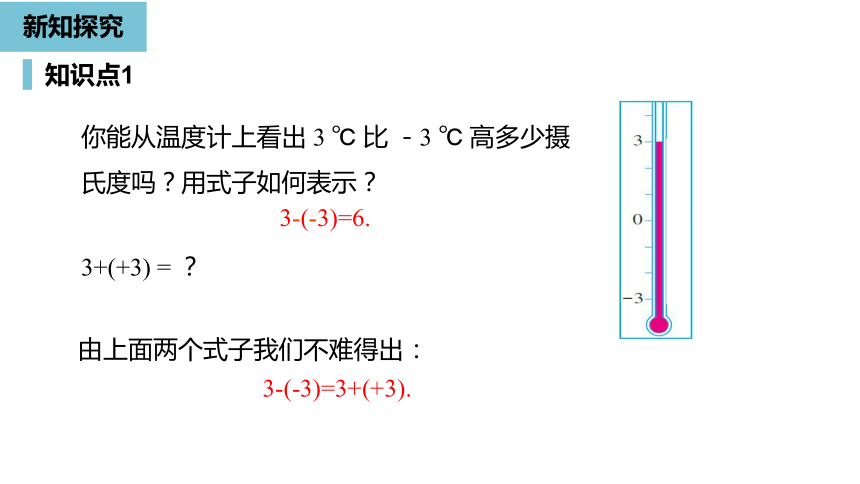
你能从温度计上看出
3
℃
比
-3
℃
高多少摄氏度吗?用式子如何表示?
3-(-3)=6.
3-(-3)=3+(+3).
3+(+3)
=
?
由上面两个式子我们不难得出:
知识点1
新知探究
用上面的方法考虑:
0-(-3)=___,
0+(+3)=___;
1-(-3)=___,
1+(+3)=___;
-5-(-3)=___,
-5+(+3)=___.
3
-2
4
-2
4
3
1
1
8
8
这些数减?3的结果与它们加+3的结果相同吗?
计算
9-8=___;
9+(-8)=____;
15-7=___;
15+(-7)=____.
知识点1
新知探究
减去一个数,等于加上这个数的相反数.
表达式为:a
-
b=a
+
(-b).
有理数减法法则
知识点1
新知探究
有理数的减法是有理数的加法的逆运算,做减法运算时,常将减法转化为加法再计算,转化过程中,应注意“两变一不变”.
“两变”是指运算符号“
-
”变成“+”,减数变成它的相反数;
“一不变”是指被减数不变.
0减去任何数都等于这个数的相反数.例如:0-2=-2,0-(-2)
=2.
知识点1
新知探究
两数相减差的符号
(1)
较大的数-较小的数=正数,即若
a>b,则
a-b>0,反之亦然.
(2)
较小的数-较大的数=负数,即若
aa-b<0,反之亦然.
(3)
相等的两个数的差为
0,即若
a=b,则
a-b=0,反之亦然.
知识点1
新知探究
(1)
(-3)-(-5);
(2)
0-7;
(3)
7.2-(-4.8);
(4)
(-3)-5
.
解:(1)
(-3)-(-5)=
(-3)+5=2.
例
计算:
(2)
0-7=0+(-7)=-7.
(3)
7.2-(-4.8)=7.2+4.8=12.
(4)
(-3)-5=-3+(-5)=-8.
跟踪训练
新知探究
口算:
(1)
6-9;
(2)
(+4)-(-7);
(3)
(-5)-(-8)
;
(4)
(-4)-9;
(5)
0-(-5);
?
(6)
0-5.
-3
3
-13
5
-5
11
随堂练习
1
计算:6-(3-5)=
.
8
随堂练习
2
某市有一天的最高气温为
2
℃,最低气温为
-8
℃
,则这天的最高气温比最低气温高(
)
A.10
℃
B.6
℃
C.
-6
℃
D.
-10
℃
A
课堂小结
减去一个数,等于加上这个数的相反数.
表达式为:a
-
b=a
+
(-b).
有理数减法法则
下列说法中正确的有(
)
①
减去一个负数等于加这个数的相反数;
②
正数减负数,差为正数;
③
0减去一个数,仍得这个数;
④
两数相减,差小于被减数;
⑤
两数相减,差不一定小于被减数;
⑥
互为相反数的两数相减差一定为0.
A.2个
B.3个
C.4个
D.5个
拓展提升
1
B
拓展提升
2
若
|x|=3,则
|x|-x
等于
.
0
或
6
拓展提升
3
已知
a,b,c,d
为有理数,其中
a,b,c,d
在数轴上的位置如图所示,试求
|a-b|-|b-c|+|c|-|b+d|
的值.
解:观察题中数轴可知,a>b,b0,b<0,d<0,
所以
a-b>0,b-c<0,|c|=c,|b+d|=-(b+d).
所以原式=(a-b)-[-(b-c)]+c-[-(b+d)]
=a-b+(b-c)+c+(b+d)
=a-b+b-c+c+b+d
=a+b+d.
1.3.2 有理数的减法
有理数
人教版-数学-七年级上册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-拓展提升
知识回顾
确定类型
定符号
绝对值
同号
异号(绝对值不相等)
异号(互为相反数)
与0相加
取相同符号
取绝对值较大的加数的符号
相加
相减
结果是0
仍是这个数
有理数的加法法则:
学习目标
1.理解、掌握有理数的减法法则,会将有理数的减法运算转化为加法运算.
2.通过把有理数的减法运算转化为加法运算,渗透转化思想,培养运算能力.
课堂导入
北京某天气温是-3?C~3?C,你能列式表示这天的温差是多少摄氏度吗?
知识点1
新知探究
你能从温度计上看出
3
℃
比
-3
℃
高多少摄氏度吗?用式子如何表示?
3-(-3)=6.
3-(-3)=3+(+3).
3+(+3)
=
?
由上面两个式子我们不难得出:
知识点1
新知探究
用上面的方法考虑:
0-(-3)=___,
0+(+3)=___;
1-(-3)=___,
1+(+3)=___;
-5-(-3)=___,
-5+(+3)=___.
3
-2
4
-2
4
3
1
1
8
8
这些数减?3的结果与它们加+3的结果相同吗?
计算
9-8=___;
9+(-8)=____;
15-7=___;
15+(-7)=____.
知识点1
新知探究
减去一个数,等于加上这个数的相反数.
表达式为:a
-
b=a
+
(-b).
有理数减法法则
知识点1
新知探究
有理数的减法是有理数的加法的逆运算,做减法运算时,常将减法转化为加法再计算,转化过程中,应注意“两变一不变”.
“两变”是指运算符号“
-
”变成“+”,减数变成它的相反数;
“一不变”是指被减数不变.
0减去任何数都等于这个数的相反数.例如:0-2=-2,0-(-2)
=2.
知识点1
新知探究
两数相减差的符号
(1)
较大的数-较小的数=正数,即若
a>b,则
a-b>0,反之亦然.
(2)
较小的数-较大的数=负数,即若
a
(3)
相等的两个数的差为
0,即若
a=b,则
a-b=0,反之亦然.
知识点1
新知探究
(1)
(-3)-(-5);
(2)
0-7;
(3)
7.2-(-4.8);
(4)
(-3)-5
.
解:(1)
(-3)-(-5)=
(-3)+5=2.
例
计算:
(2)
0-7=0+(-7)=-7.
(3)
7.2-(-4.8)=7.2+4.8=12.
(4)
(-3)-5=-3+(-5)=-8.
跟踪训练
新知探究
口算:
(1)
6-9;
(2)
(+4)-(-7);
(3)
(-5)-(-8)
;
(4)
(-4)-9;
(5)
0-(-5);
?
(6)
0-5.
-3
3
-13
5
-5
11
随堂练习
1
计算:6-(3-5)=
.
8
随堂练习
2
某市有一天的最高气温为
2
℃,最低气温为
-8
℃
,则这天的最高气温比最低气温高(
)
A.10
℃
B.6
℃
C.
-6
℃
D.
-10
℃
A
课堂小结
减去一个数,等于加上这个数的相反数.
表达式为:a
-
b=a
+
(-b).
有理数减法法则
下列说法中正确的有(
)
①
减去一个负数等于加这个数的相反数;
②
正数减负数,差为正数;
③
0减去一个数,仍得这个数;
④
两数相减,差小于被减数;
⑤
两数相减,差不一定小于被减数;
⑥
互为相反数的两数相减差一定为0.
A.2个
B.3个
C.4个
D.5个
拓展提升
1
B
拓展提升
2
若
|x|=3,则
|x|-x
等于
.
0
或
6
拓展提升
3
已知
a,b,c,d
为有理数,其中
a,b,c,d
在数轴上的位置如图所示,试求
|a-b|-|b-c|+|c|-|b+d|
的值.
解:观察题中数轴可知,a>b,b
所以
a-b>0,b-c<0,|c|=c,|b+d|=-(b+d).
所以原式=(a-b)-[-(b-c)]+c-[-(b+d)]
=a-b+(b-c)+c+(b+d)
=a-b+b-c+c+b+d
=a+b+d.
