人教版九年级下册数学 27.2.3相似三角形应用举例课件(共25张PPT)
文档属性
| 名称 | 人教版九年级下册数学 27.2.3相似三角形应用举例课件(共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-20 10:11:15 | ||
图片预览






文档简介
(共25张PPT)
27.2
.3相似三角形应用举例(1)
人教版九年级(下册)第二十七章
1、判定三角形相似的方法:
方法1:定义法
方法5:两角对应相等.(AA)
方法6:斜边直角边对应成比例.(HL)
方法2:(平行法)平行于三角形一边的直线和其它两边相交
,
所构成的三角形与原三角形相似。
方法3:三边对应成比例.(SSS)
方法4:两边对应成比例且夹角相等.(SAS)
知识回顾
2、相似三角形的性质:
(1)三角对应相等,三边对应成比例.
(2)对应线段的比等于相似比(对应中线的比、对应高
的比、对应角平分线的比都等于相似比.)
(3)周长的比等于相似比.
(4)面积的比等于相似比的平方.
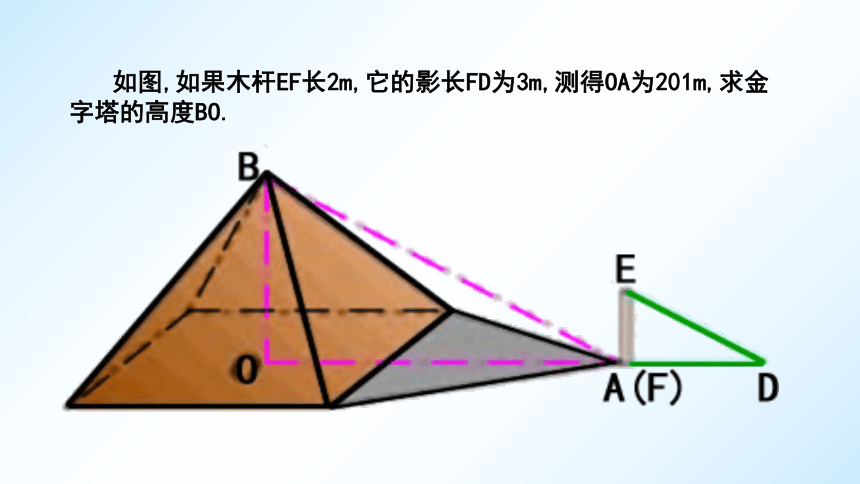
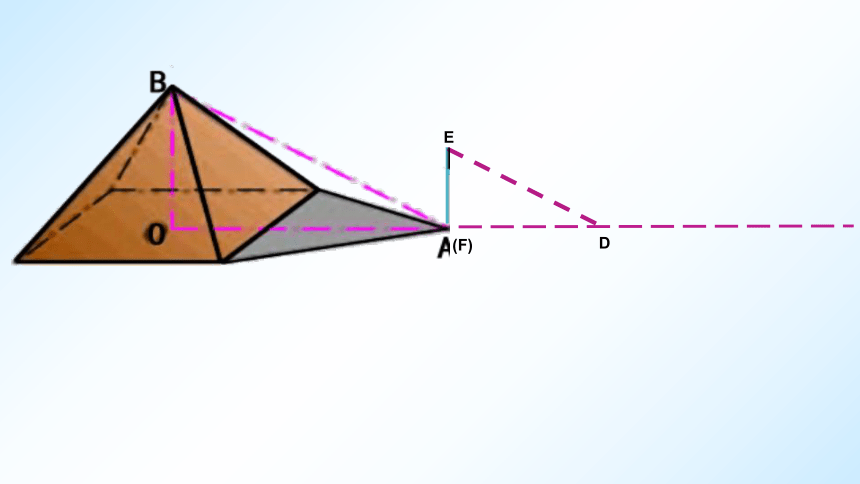
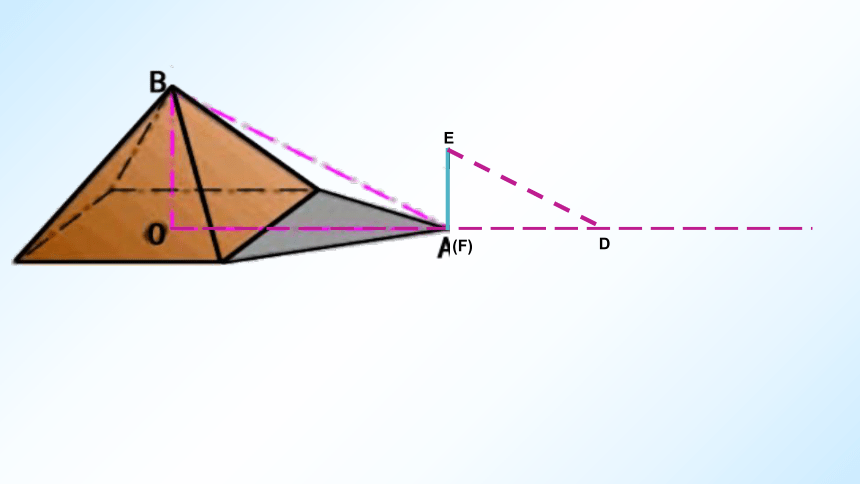
例1.据史料记载,古希腊数学家,天文学家泰勒斯曾利用相似三角形的原理,在金字塔影子的顶部立一根木杆.借助太阳光线构成两个相似三角形,来测量金字塔的高度.
如图,如果木杆EF长2m,它的影长FD为3m,测得OA为201m,求金字塔的高度BO.
例2、如图,为了估算河的宽度,我们可以在河对岸选定一个目标点P,在河的这一边取点Q和S,使点P、Q、S共线且直线PS与河垂直,接着在过点S且与PS垂直的直线a上选择适当的点T,确定PT与过点Q且垂直PS的直线b的交点为R.如果测得QS=45m,ST=90m,QR=60m,求河的宽度PQ.
解:∵∠PQR=∠PST=90°,∠P=∠P
∴△PQR∽△PST
因此河宽大约为90m.
如图,为了估算河的宽度,我们也可以在河对岸选定一个目标作为点P,再在河的这一边选点Q和点S,使PQ⊥QS,然后,再选点R,使RS⊥QS,用视线确定PR和QS的交点T,分别测出
QT,TS,RS的长度即可求出PQ.?
1、如图,九年级某班数学兴趣小组的同学想利用所学数学知识测量学校旗杆的高度,当身高1.6米的楚阳同学站在C处时,他头顶端的影子正好与旗杆顶端的影子重合,同一时刻,其他成员测得AC=2米,BC=10米,则旗杆的高度是______米.
9.6
2、在某一时刻,测得一根高为1.8m的竹竿的影长为3m,同时测得一栋高楼的影长为90m,这栋高楼的高度是
m.
54
针对训练
3、如图是小明设计用手电来测量某古城墙高度的示意图,点P处放一水平的平面镜,光线从点A出发经平面镜反射后,刚好射到古城墙的顶端C处,已知AB=2米,且测得BP=3米,DP=12米,那么该古城
墙的高度是(
)
A.
6米
B.
8米
C.
18米
D.
24米
B
4、如图,铁道口的栏杆短臂长1m,长臂长16m,当短臂端点下降0.5m时,长臂端点升高
m。
8
1、如图,△ABC是一块锐角三角形余料,边BC=120毫米,高AD=80毫米,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?
拓展训练
拓展训练
2、某同学想利用树影测量树高.他在某一时刻测得小树EF高为1.5米时,其影长FG为1.2米,当他测量教学楼旁的一棵大树AB影长时,因大树靠近教学楼,有一部分影子在墙上.经测量,地面部分影长BC为6.4米,墙上影长CD为1.4米,那么这棵大树AB高多少米?
课堂小结
1.在实际生活中,
我们面对不能直接测量物体的高度和宽度时.
可以把它们转化为数学问题,建立相似三角形模型,再利用对应边的比相等来达到求解的目的!
2.掌握并应用一些简单的相似三角形模型.
1、课本43页第8,9,10题.
2、学案上的课后练习
课后作业
27.2
.3相似三角形应用举例(1)
人教版九年级(下册)第二十七章
1、判定三角形相似的方法:
方法1:定义法
方法5:两角对应相等.(AA)
方法6:斜边直角边对应成比例.(HL)
方法2:(平行法)平行于三角形一边的直线和其它两边相交
,
所构成的三角形与原三角形相似。
方法3:三边对应成比例.(SSS)
方法4:两边对应成比例且夹角相等.(SAS)
知识回顾
2、相似三角形的性质:
(1)三角对应相等,三边对应成比例.
(2)对应线段的比等于相似比(对应中线的比、对应高
的比、对应角平分线的比都等于相似比.)
(3)周长的比等于相似比.
(4)面积的比等于相似比的平方.
例1.据史料记载,古希腊数学家,天文学家泰勒斯曾利用相似三角形的原理,在金字塔影子的顶部立一根木杆.借助太阳光线构成两个相似三角形,来测量金字塔的高度.
如图,如果木杆EF长2m,它的影长FD为3m,测得OA为201m,求金字塔的高度BO.
例2、如图,为了估算河的宽度,我们可以在河对岸选定一个目标点P,在河的这一边取点Q和S,使点P、Q、S共线且直线PS与河垂直,接着在过点S且与PS垂直的直线a上选择适当的点T,确定PT与过点Q且垂直PS的直线b的交点为R.如果测得QS=45m,ST=90m,QR=60m,求河的宽度PQ.
解:∵∠PQR=∠PST=90°,∠P=∠P
∴△PQR∽△PST
因此河宽大约为90m.
如图,为了估算河的宽度,我们也可以在河对岸选定一个目标作为点P,再在河的这一边选点Q和点S,使PQ⊥QS,然后,再选点R,使RS⊥QS,用视线确定PR和QS的交点T,分别测出
QT,TS,RS的长度即可求出PQ.?
1、如图,九年级某班数学兴趣小组的同学想利用所学数学知识测量学校旗杆的高度,当身高1.6米的楚阳同学站在C处时,他头顶端的影子正好与旗杆顶端的影子重合,同一时刻,其他成员测得AC=2米,BC=10米,则旗杆的高度是______米.
9.6
2、在某一时刻,测得一根高为1.8m的竹竿的影长为3m,同时测得一栋高楼的影长为90m,这栋高楼的高度是
m.
54
针对训练
3、如图是小明设计用手电来测量某古城墙高度的示意图,点P处放一水平的平面镜,光线从点A出发经平面镜反射后,刚好射到古城墙的顶端C处,已知AB=2米,且测得BP=3米,DP=12米,那么该古城
墙的高度是(
)
A.
6米
B.
8米
C.
18米
D.
24米
B
4、如图,铁道口的栏杆短臂长1m,长臂长16m,当短臂端点下降0.5m时,长臂端点升高
m。
8
1、如图,△ABC是一块锐角三角形余料,边BC=120毫米,高AD=80毫米,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?
拓展训练
拓展训练
2、某同学想利用树影测量树高.他在某一时刻测得小树EF高为1.5米时,其影长FG为1.2米,当他测量教学楼旁的一棵大树AB影长时,因大树靠近教学楼,有一部分影子在墙上.经测量,地面部分影长BC为6.4米,墙上影长CD为1.4米,那么这棵大树AB高多少米?
课堂小结
1.在实际生活中,
我们面对不能直接测量物体的高度和宽度时.
可以把它们转化为数学问题,建立相似三角形模型,再利用对应边的比相等来达到求解的目的!
2.掌握并应用一些简单的相似三角形模型.
1、课本43页第8,9,10题.
2、学案上的课后练习
课后作业
