人教版数学七年级上册2.1整式(3)课件(17张PPT)
文档属性
| 名称 | 人教版数学七年级上册2.1整式(3)课件(17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 243.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-19 22:18:53 | ||
图片预览





文档简介
(共17张PPT)
2.1 整式
整式的加减
人教版-数学-七年级上册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-拓展提升
知识回顾
1.什么叫单项式?
2.怎么确定一个单项式的系数和次数?
如果一个式子是数或字母的积,那么这个式子叫做单项式.
系数
次数
单项式中的数字因数;
所有字母的指数的和.
学习目标
1.理解多项式、整式的概念.
2.会确定一个多项式的项数和次数.
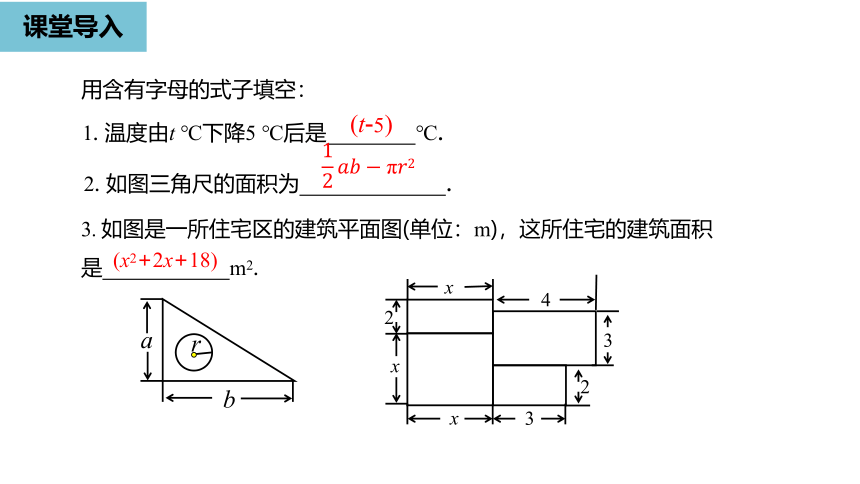
课堂导入
1.
温度由t
℃下降5
℃后是
℃.
(t-5)
2.
如图三角尺的面积为
.
3.
如图是一所住宅区的建筑平面图(单位:m),这所住宅的建筑面积
是
m2.
(x2+2x+18)
a
b
r
x
x
x
2
4
3
2
3
用含有字母的式子填空:
知识点1
新知探究
3x+5y+2z
x2+2x+18
t-5
观察下面这些式子,它们是单项式吗?这些式子有什么共同特点?与单项式有什么关系?
上述几个式子都是两个或者多个单项式相加的形式.
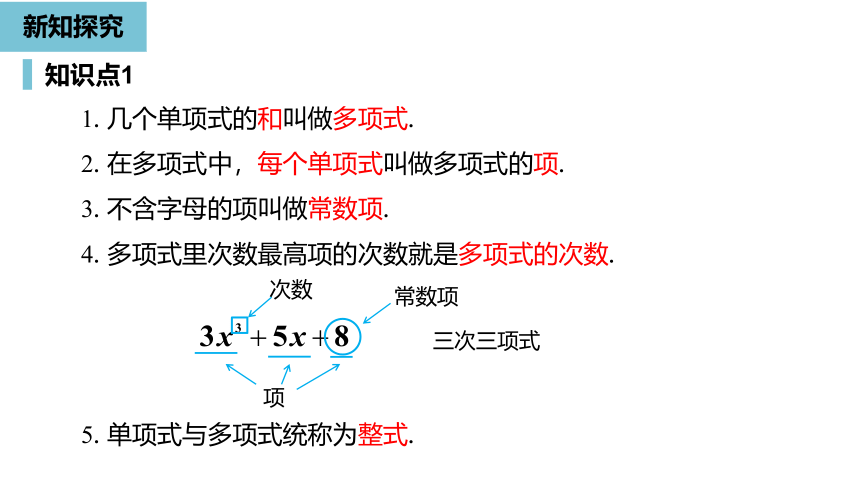
知识点1
新知探究
1.
几个单项式的和叫做多项式.
2.
在多项式中,每个单项式叫做多项式的项.
3.
不含字母的项叫做常数项.
4.
多项式里次数最高项的次数就是多项式的次数.
5.
单项式与多项式统称为整式.
次数
三次三项式
常数项
项
知识点1
新知探究
整式、单项式、多项式之间的关系:
多项式由几个单项式的和组成;
所有的单项式与多项式都是整式;
既不是单项式也不是多项式的式子一定不是整式.
知识点1
新知探究
(1)多项式的各项应包括它前面的符号;
(3)要确定一个多项式的次数,先要确定此多项式中各项(单项式)的次数,然后找次数最高的;
(4)一个多项式的最高次项可以不唯一.
(2)多项式没有系数的概念,但其每一项均有系数,每一项的系数也包括前面的符号;
知识点1
新知探究
例
如图,用式子表示圆环的面积.当R=15
cm,r=10
cm
时,求圆环的面积(π取3.14).
解:外圆的面积减去内圆的面积就是圆环的面积,所以圆环的面积是πR2-πr2
.
当R=15
cm,r=10
cm时,圆环的面积(单位:cm2)是
πR2-πr2
=3.14×152-3.14×102=392.5(cm2).
跟踪训练
新知探究
指出下列各式中,哪些是单项式,哪些是多项式,哪些是整式.
x-3,,8-,,x2-
+1,,-6,.
解:单项式有:,-6,.
多项式有:x-3,,x2-
+1.
整式有:x-3,,,x2-
+1,,-6,.
随堂练习
1
下列说法中正确的是(
)
A.的系数是-2
B.32ab3的系数是9
C.3x2y3+2xy+1的系数是3
D.x2+x-1的常数项是1
B
随堂练习
2
一个只含有y的二次三项式,它的二次项系数为-1,一次项系数为2,常数项为7,则这个二次三项式为(
)
A.
-y2
+2y-7
B.y2
-2y-7
C.
-y2
+2y+7
D.y2-2y+7
C
随堂练习
3
已知多项式-xym+1+x3y-2x3+(n+1)x+3是关于x,y的六次四项式,求m-n的值.
解:因为多项式-xym+1+x3y-2x3+(n+1)x+3是关于x,y的六次四项式,
所以1+m+1=6,n+1=0,
解得m=4,n=-1,所以m-n=4-(-1)=5.
课堂小结
(其中不含字母的项叫做常数项)
次数:多项式中次数最高的项的次数.
项:式中的每个单项式叫多项式的项.
次数:所有字母的指数和
系数:数字因数
单项式
多项式
整式
拓展提升
1
若2m+n=4,则6-2m-n
的值为
.
2
拓展提升
2
当x=1时,式子ax3-3bx+4的值是7,则当x=-1时,这个式子的值是(
)
A.7
B.3
C.1
D.-7
C
拓展提升
3
已知多项式-8x2ym+2-xy3+x是关于x,y的七次多项式,关于x,y的单项式6x2nym+2与该多项式的次数相同,求(n-
m)3的值.
解:因为多项式-8x2ym+2-xy3+x是关于x,y的七次多项式,
所以2+m+2=7,解得m=3.
因为关于x,y的单项式6x2nym+2与该多项式的次数相同,
所以2n+m+2=7,把m=3代入,得2n+3+2=7,解得n=1.
所以(n-m)3=(1-3)3=(-2)3=-8.
2.1 整式
整式的加减
人教版-数学-七年级上册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-拓展提升
知识回顾
1.什么叫单项式?
2.怎么确定一个单项式的系数和次数?
如果一个式子是数或字母的积,那么这个式子叫做单项式.
系数
次数
单项式中的数字因数;
所有字母的指数的和.
学习目标
1.理解多项式、整式的概念.
2.会确定一个多项式的项数和次数.
课堂导入
1.
温度由t
℃下降5
℃后是
℃.
(t-5)
2.
如图三角尺的面积为
.
3.
如图是一所住宅区的建筑平面图(单位:m),这所住宅的建筑面积
是
m2.
(x2+2x+18)
a
b
r
x
x
x
2
4
3
2
3
用含有字母的式子填空:
知识点1
新知探究
3x+5y+2z
x2+2x+18
t-5
观察下面这些式子,它们是单项式吗?这些式子有什么共同特点?与单项式有什么关系?
上述几个式子都是两个或者多个单项式相加的形式.
知识点1
新知探究
1.
几个单项式的和叫做多项式.
2.
在多项式中,每个单项式叫做多项式的项.
3.
不含字母的项叫做常数项.
4.
多项式里次数最高项的次数就是多项式的次数.
5.
单项式与多项式统称为整式.
次数
三次三项式
常数项
项
知识点1
新知探究
整式、单项式、多项式之间的关系:
多项式由几个单项式的和组成;
所有的单项式与多项式都是整式;
既不是单项式也不是多项式的式子一定不是整式.
知识点1
新知探究
(1)多项式的各项应包括它前面的符号;
(3)要确定一个多项式的次数,先要确定此多项式中各项(单项式)的次数,然后找次数最高的;
(4)一个多项式的最高次项可以不唯一.
(2)多项式没有系数的概念,但其每一项均有系数,每一项的系数也包括前面的符号;
知识点1
新知探究
例
如图,用式子表示圆环的面积.当R=15
cm,r=10
cm
时,求圆环的面积(π取3.14).
解:外圆的面积减去内圆的面积就是圆环的面积,所以圆环的面积是πR2-πr2
.
当R=15
cm,r=10
cm时,圆环的面积(单位:cm2)是
πR2-πr2
=3.14×152-3.14×102=392.5(cm2).
跟踪训练
新知探究
指出下列各式中,哪些是单项式,哪些是多项式,哪些是整式.
x-3,,8-,,x2-
+1,,-6,.
解:单项式有:,-6,.
多项式有:x-3,,x2-
+1.
整式有:x-3,,,x2-
+1,,-6,.
随堂练习
1
下列说法中正确的是(
)
A.的系数是-2
B.32ab3的系数是9
C.3x2y3+2xy+1的系数是3
D.x2+x-1的常数项是1
B
随堂练习
2
一个只含有y的二次三项式,它的二次项系数为-1,一次项系数为2,常数项为7,则这个二次三项式为(
)
A.
-y2
+2y-7
B.y2
-2y-7
C.
-y2
+2y+7
D.y2-2y+7
C
随堂练习
3
已知多项式-xym+1+x3y-2x3+(n+1)x+3是关于x,y的六次四项式,求m-n的值.
解:因为多项式-xym+1+x3y-2x3+(n+1)x+3是关于x,y的六次四项式,
所以1+m+1=6,n+1=0,
解得m=4,n=-1,所以m-n=4-(-1)=5.
课堂小结
(其中不含字母的项叫做常数项)
次数:多项式中次数最高的项的次数.
项:式中的每个单项式叫多项式的项.
次数:所有字母的指数和
系数:数字因数
单项式
多项式
整式
拓展提升
1
若2m+n=4,则6-2m-n
的值为
.
2
拓展提升
2
当x=1时,式子ax3-3bx+4的值是7,则当x=-1时,这个式子的值是(
)
A.7
B.3
C.1
D.-7
C
拓展提升
3
已知多项式-8x2ym+2-xy3+x是关于x,y的七次多项式,关于x,y的单项式6x2nym+2与该多项式的次数相同,求(n-
m)3的值.
解:因为多项式-8x2ym+2-xy3+x是关于x,y的七次多项式,
所以2+m+2=7,解得m=3.
因为关于x,y的单项式6x2nym+2与该多项式的次数相同,
所以2n+m+2=7,把m=3代入,得2n+3+2=7,解得n=1.
所以(n-m)3=(1-3)3=(-2)3=-8.
