人教版数学七年级上册2.2整式的加减(1)课件(26张PPT)
文档属性
| 名称 | 人教版数学七年级上册2.2整式的加减(1)课件(26张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 241.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-19 22:21:29 | ||
图片预览








文档简介
(共26张PPT)
2.2 整式的加减
整式的加减
人教版-数学-七年级上册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-拓展提升
知识回顾
(其中不含字母的项叫做常数项)
次数:多项式中次数最高项的次数.
项:式中的每个单项式叫多项式的项.
次数:所有字母的指数和
系数:数字因数
单项式
多项式
整式
学习目标
1.知道同类项的概念,会识别同类项.
2.掌握合并同类项的法则,并能准确合并同类项.
3.能在合并同类项的基础上进行化简、求值运算.
课堂导入
如果有一罐硬币(分别为一角、五角、一元的),你会如何去数呢?
知识点1
新知探究
8n
5n
3ab2
-ab2
6xy
-3xy
-7a2b
2a2b
观察下列各组单项式有什么特点?
1.所含字母相同.
2.相同字母的指数也相同.
知识点1
新知探究
所含字母相同,并且相同字母的指数也相同的项叫做同类项.
几个常数项也是同类项.
(1)是不是同类项有“两个无关”:①与系数无关;②与字母的排列顺序无关,如3mn与-nm是同类项;
(2)同类项都是单项式.
知识点1
新知探究
抓住“两个相同”:一是所含的字母要完全相同,二是相同字母的指数要相同,这两个条件缺一不可.
同类项的判别方法:
跟踪训练
新知探究
下列各组单项式:①y与y2
;②-a2b3与2a2b3
;③2x2y与5yx2;
④-2
019与0.其中是同类项的有(
)
A.4组
B.3组
C.2组
D.1组
B
知识点2
新知探究
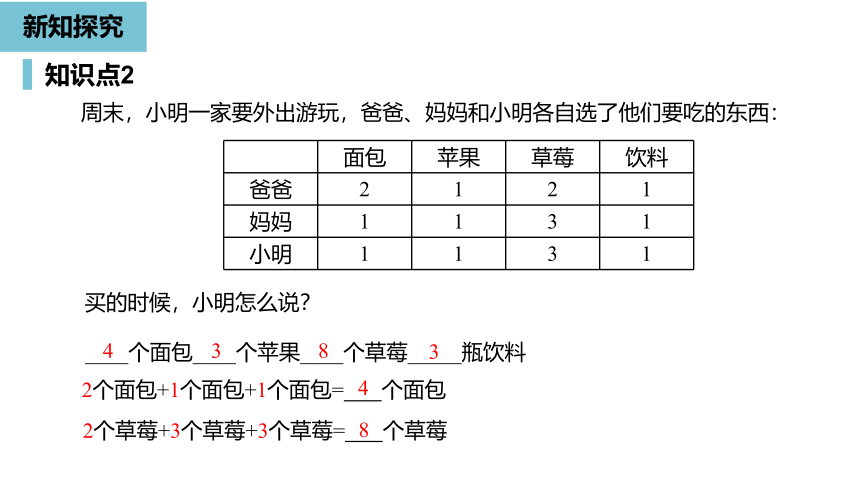
周末,小明一家要外出游玩,爸爸、妈妈和小明各自选了他们要吃的东西:
买的时候,小明怎么说?
____个面包____个苹果____个草莓_____瓶饮料
4
2个面包+1个面包+1个面包=
个面包
2个草莓+3个草莓+3个草莓=
个草莓
4
8
面包
苹果
草莓
饮料
爸爸
2
1
2
1
妈妈
1
1
3
1
小明
1
1
3
1
3
8
3
知识点2
新知探究
合并同类项的法则:
合并同类项后,所得项的系数是合并前各同类项的系数的和,且字母连同它的指数不变.
把多项式中的同类项合并成一项,叫做合并同类项.
3
ab?+
5
ab?
=
8
ab?
相加
不变
知识点2
新知探究
合并同类项的一般步骤:
一找:找出同类项,当项数较多时,通常在同类项的下面做相同的标记;
二移:运用加法交换律、结合律将多项式中的同类项结合;
三合:利用合并同类项法则,合并同类项;
四排:合并后的结果按某一个字母的降幂(或升幂)排列.
知识点2
新知探究
1.合并同类项时,只能把同类项合并成一项,不是同类项的不能合并,不能合并的项,在每一步运算中都要写出,不能漏掉.
2.所有的常数项都是同类项,合并时把它们结合在一起,运用有理数的运算法则进行合并.
3.若两个同类项的系数互为相反数,则合并同类项的结果为0.
知识点2
新知探究
活学巧记
合并同类项,
法则不能忘,
只求系数和,
字母、指数不变样.
知识点2
新知探究
例合并下列各式的同类项:
(1)xy2-xy2;(2)-3x2y+2x2y+3xy2-2xy2;(3)4a2
+
3b2
+2ab-4a2
-4b2.
解:(1)
xy2-xy2=(
1-)xy2=xy2.
(2)
-3x2y+2x2y+3xy2
-
2xy2
=(-3+2)
x2y+(3-2)
xy2
=-
x2y+xy2.
知识点2
新知探究
解:(3)
4a2
+
3b2
+2ab-4a2
-4b2
=
(4a2-4a2)
+
(
3b2
-4b2)
+
2ab
=
(4-4)a2
+
(3-4)b2
+
2ab
=-b2
+
2ab.
例合并下列各式的同类项:
(1)xy2-xy2;(2)-3x2y+2x2y+3xy2-2xy2;(3)4a2
+
3b2
+2ab-4a2
-4b2.
知识点2
新知探究
合并同类项时要注意“一相加,两不变”,“一相加”是指各同类项的系数相加;“两不变”是指字母连同它的指数不变.
知识点2
新知探究
例(1)求多项式
2x2-5x+x2+4x-3x2-2
的值,其中x=;
(2)求多项式
3a+abc-c2-3a+c2的值,其中
a=,b=2,c=-3.
分析:在求多项式的值时,可以先将多项式中的同类项合并,然后再求值,这样做往往可以简化计算.
知识点2
新知探究
解:
(1)
2x2-5x+x2+4x-3x2-2
=
(2+1-3)
x2
+
(-5+4)
x-2
=-x-2.
当
x=时,原式=2=-.
例(1)求多项式
2x2-5x+x2+4x-3x2-2
的值,其中x=;
(2)求多项式
3a+abc-c2-3a+c2的值,其中
a=,b=2,c=-3.
知识点2
新知探究
解:
例(1)求多项式
2x2-5x+x2+4x-3x2-2
的值,其中x=;
(2)求多项式
3a+abc-c2-3a+c2的值,其中
a=,b=2,c=-3.
跟踪训练
新知探究
计算:xy2-5y3-2xy2+5y3.
解:xy2-5y3-2xy2+5y3
=(xy2
-2xy2)+(-5y3
+5y3)
=(1-2)xy2
+(-5+5)y3
=-xy2.
随堂练习
1
若单项式
am-1b2
与
a2bn
的和仍是单项式,则
nm
的值是(
)
A.3
B.6
C.8
D.9
C
随堂练习
2
计算3x2-x2的结果是(
)
A.2
B.2x2
C.2x
D.4x2
B
随堂练习
3
水库中水位第一天连续下降了a小时,每小时平均下降2
cm;第二天连续上升了a小时,每小时平均上升0.5
cm,这两天水位总的变化情况如何?
解:把下降的水位变化量记为负,上升的水位变化量记为正.
第一天水位的变化量是-2a
cm,第二天水位的变化量是0.5a
cm.
两天水位的总变化量(单位:cm)是
-2a+0.5a=(-2+0.5)a=-1.5a(cm).
这两天水位总的变化情况为下降了1.5a
cm.
课堂小结
同
类
项
合并同类项
法则
(1)字母相同;
(1)系数相加;
(2)字母连同它的指数不变.
步骤
一找、二移、三合、四排
(一加两不变)
两无关
两相同
(2)相同字母的指数相同.
拓展提升
1
若单项式
2x2ym
与-xny4可以合并成一项,则
nm
=.
16
拓展提升
2
合并同类项:3a2b-2ab+2+2ab-a2b-5.
解:
3a2b-2ab+2+2ab-a2b-5
=
(3a2b-a2b)+(-2ab+2ab)+2-5
=2a2b-3.
2.2 整式的加减
整式的加减
人教版-数学-七年级上册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-拓展提升
知识回顾
(其中不含字母的项叫做常数项)
次数:多项式中次数最高项的次数.
项:式中的每个单项式叫多项式的项.
次数:所有字母的指数和
系数:数字因数
单项式
多项式
整式
学习目标
1.知道同类项的概念,会识别同类项.
2.掌握合并同类项的法则,并能准确合并同类项.
3.能在合并同类项的基础上进行化简、求值运算.
课堂导入
如果有一罐硬币(分别为一角、五角、一元的),你会如何去数呢?
知识点1
新知探究
8n
5n
3ab2
-ab2
6xy
-3xy
-7a2b
2a2b
观察下列各组单项式有什么特点?
1.所含字母相同.
2.相同字母的指数也相同.
知识点1
新知探究
所含字母相同,并且相同字母的指数也相同的项叫做同类项.
几个常数项也是同类项.
(1)是不是同类项有“两个无关”:①与系数无关;②与字母的排列顺序无关,如3mn与-nm是同类项;
(2)同类项都是单项式.
知识点1
新知探究
抓住“两个相同”:一是所含的字母要完全相同,二是相同字母的指数要相同,这两个条件缺一不可.
同类项的判别方法:
跟踪训练
新知探究
下列各组单项式:①y与y2
;②-a2b3与2a2b3
;③2x2y与5yx2;
④-2
019与0.其中是同类项的有(
)
A.4组
B.3组
C.2组
D.1组
B
知识点2
新知探究
周末,小明一家要外出游玩,爸爸、妈妈和小明各自选了他们要吃的东西:
买的时候,小明怎么说?
____个面包____个苹果____个草莓_____瓶饮料
4
2个面包+1个面包+1个面包=
个面包
2个草莓+3个草莓+3个草莓=
个草莓
4
8
面包
苹果
草莓
饮料
爸爸
2
1
2
1
妈妈
1
1
3
1
小明
1
1
3
1
3
8
3
知识点2
新知探究
合并同类项的法则:
合并同类项后,所得项的系数是合并前各同类项的系数的和,且字母连同它的指数不变.
把多项式中的同类项合并成一项,叫做合并同类项.
3
ab?+
5
ab?
=
8
ab?
相加
不变
知识点2
新知探究
合并同类项的一般步骤:
一找:找出同类项,当项数较多时,通常在同类项的下面做相同的标记;
二移:运用加法交换律、结合律将多项式中的同类项结合;
三合:利用合并同类项法则,合并同类项;
四排:合并后的结果按某一个字母的降幂(或升幂)排列.
知识点2
新知探究
1.合并同类项时,只能把同类项合并成一项,不是同类项的不能合并,不能合并的项,在每一步运算中都要写出,不能漏掉.
2.所有的常数项都是同类项,合并时把它们结合在一起,运用有理数的运算法则进行合并.
3.若两个同类项的系数互为相反数,则合并同类项的结果为0.
知识点2
新知探究
活学巧记
合并同类项,
法则不能忘,
只求系数和,
字母、指数不变样.
知识点2
新知探究
例合并下列各式的同类项:
(1)xy2-xy2;(2)-3x2y+2x2y+3xy2-2xy2;(3)4a2
+
3b2
+2ab-4a2
-4b2.
解:(1)
xy2-xy2=(
1-)xy2=xy2.
(2)
-3x2y+2x2y+3xy2
-
2xy2
=(-3+2)
x2y+(3-2)
xy2
=-
x2y+xy2.
知识点2
新知探究
解:(3)
4a2
+
3b2
+2ab-4a2
-4b2
=
(4a2-4a2)
+
(
3b2
-4b2)
+
2ab
=
(4-4)a2
+
(3-4)b2
+
2ab
=-b2
+
2ab.
例合并下列各式的同类项:
(1)xy2-xy2;(2)-3x2y+2x2y+3xy2-2xy2;(3)4a2
+
3b2
+2ab-4a2
-4b2.
知识点2
新知探究
合并同类项时要注意“一相加,两不变”,“一相加”是指各同类项的系数相加;“两不变”是指字母连同它的指数不变.
知识点2
新知探究
例(1)求多项式
2x2-5x+x2+4x-3x2-2
的值,其中x=;
(2)求多项式
3a+abc-c2-3a+c2的值,其中
a=,b=2,c=-3.
分析:在求多项式的值时,可以先将多项式中的同类项合并,然后再求值,这样做往往可以简化计算.
知识点2
新知探究
解:
(1)
2x2-5x+x2+4x-3x2-2
=
(2+1-3)
x2
+
(-5+4)
x-2
=-x-2.
当
x=时,原式=2=-.
例(1)求多项式
2x2-5x+x2+4x-3x2-2
的值,其中x=;
(2)求多项式
3a+abc-c2-3a+c2的值,其中
a=,b=2,c=-3.
知识点2
新知探究
解:
例(1)求多项式
2x2-5x+x2+4x-3x2-2
的值,其中x=;
(2)求多项式
3a+abc-c2-3a+c2的值,其中
a=,b=2,c=-3.
跟踪训练
新知探究
计算:xy2-5y3-2xy2+5y3.
解:xy2-5y3-2xy2+5y3
=(xy2
-2xy2)+(-5y3
+5y3)
=(1-2)xy2
+(-5+5)y3
=-xy2.
随堂练习
1
若单项式
am-1b2
与
a2bn
的和仍是单项式,则
nm
的值是(
)
A.3
B.6
C.8
D.9
C
随堂练习
2
计算3x2-x2的结果是(
)
A.2
B.2x2
C.2x
D.4x2
B
随堂练习
3
水库中水位第一天连续下降了a小时,每小时平均下降2
cm;第二天连续上升了a小时,每小时平均上升0.5
cm,这两天水位总的变化情况如何?
解:把下降的水位变化量记为负,上升的水位变化量记为正.
第一天水位的变化量是-2a
cm,第二天水位的变化量是0.5a
cm.
两天水位的总变化量(单位:cm)是
-2a+0.5a=(-2+0.5)a=-1.5a(cm).
这两天水位总的变化情况为下降了1.5a
cm.
课堂小结
同
类
项
合并同类项
法则
(1)字母相同;
(1)系数相加;
(2)字母连同它的指数不变.
步骤
一找、二移、三合、四排
(一加两不变)
两无关
两相同
(2)相同字母的指数相同.
拓展提升
1
若单项式
2x2ym
与-xny4可以合并成一项,则
nm
=.
16
拓展提升
2
合并同类项:3a2b-2ab+2+2ab-a2b-5.
解:
3a2b-2ab+2+2ab-a2b-5
=
(3a2b-a2b)+(-2ab+2ab)+2-5
=2a2b-3.
