人教版数学七年级上册3.1.1一元一次方程(2)课件(15张PPT)
文档属性
| 名称 | 人教版数学七年级上册3.1.1一元一次方程(2)课件(15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 164.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-19 22:25:19 | ||
图片预览






文档简介
(共15张PPT)
3.1.1 一元一次方程
一元一次方程
人教版-数学-七年级上册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-拓展提升
知识回顾
只含有一个未知数
未知数的次数都是1
等号两边都是整式
一元一次方程
学习目标
掌握一元一次方程的解的概念,学会判断某个数值是不是一元一次方程的解.
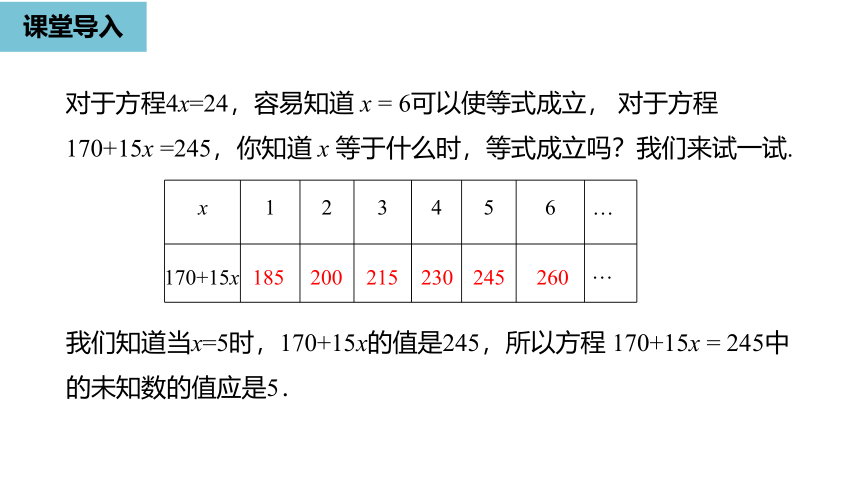
课堂导入
对于方程4x=24,容易知道
x
=
6可以使等式成立,
对于方程
170+15x
=245,你知道
x
等于什么时,等式成立吗?我们来试一试.
x
1
2
3
4
5
6
…
…
我们知道当x=5时,170+15x的值是245,所以方程
170+15x
=
245中的未知数的值应是5.
185
200
215
230
245
260
170+15x
知识点1
新知探究
使方程左右两边相等的未知数的值叫方程的解.
求方程解的过程叫做解方程.
x=420是
方程的解吗?
方程的解
知识点1
新知探究
x=1000和
x=2000中哪一个是方程
0.52x-(1-0.52)x=80的解?
解:当x=1000时,
方程左边=0.52×1000-(1-0.52)×1000=520-480=40,
右边=80,左边≠右边,所以x=1000不是此方程的解.
当x=2000时,
方程左边=
0.52×2000-(1-0.52)×2000=1040-960=80,
右边=80,左边=右边,所以x=2000是此方程的解.
知识点1
新知探究
1.
将数值代入方程左边进行计算.
2.
将数值代入方程右边进行计算.
3.
若左边=右边,则是方程的解,反之,则不是.
判断一个数值是不是方程的解的步骤:
知识点1
新知探究
方程的解与解方程的关系
(1)
方程的解与解方程是两个不同的概念,方程的解是一个具体的数值,而解方程是求方程的解的过程;
(2)
方程的解是通过解方程求得的.
知识点1
(1)
方程的解可能有多个,也可能无解,如x=1和x=2都是方程x2-3x+2=0的解,而方程|x|=-2无解.
(2)
检验一个数是不是方程的解,不能将所给的数直接代入方程中,而是要把这个数分别代入方程的左右两边,当左边=右边时,这个数是方程的解,当左边≠右边时,这个数不是方程的解.
新知探究
跟踪训练
检验
x=2是不是方程
2x-1=1+x
的解.
解:将x=2代入方程的左边,得2×2-1
=3,
将x=2代入方程的右边,得1+2=3.
因为左边=右边,
所以
x=2是方程2x-1=1+x的解.
新知探究
随堂练习
1
x=3,x=0,x=-2,各是下列哪个方程的解?
(1)
5x+7=7-2x;
(2)
6x-8=8x-4;
(3)
3x-2=4+x.
x=0
x=-2
x=3
随堂练习
2
已知关于
x
的一元一次方程2(x-1)+3a=3的解为4,则
a
的值是(
)
A.-1
B.1
C.-2
D.-3
解析:将x=4代入2(x-1)+3a=3,
得2×3+3a=3,
解得
a=
-1.
A
根据方程的解的定义求有关字母的值时,通常先让解“回家”,即将解代入方程中,得到关于字母的方程,求解即可得到这个字母的值.
课堂小结
使方程左右两边相等的未知数的值叫方程的解.
求方程解的过程叫做解方程.
方程的解
拓展提升
1
x
=1是下列哪个方程的解(
)
A.
1-x=2
B.2x-1=4-3x
C.
D.
x-4=5x-2
B
拓展提升
2
若
x=2是关于
x的方程的解,则.
解:将x=2代入方程,得2-2a=1+3,
解得
a=-1,
所以.
0
3.1.1 一元一次方程
一元一次方程
人教版-数学-七年级上册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-拓展提升
知识回顾
只含有一个未知数
未知数的次数都是1
等号两边都是整式
一元一次方程
学习目标
掌握一元一次方程的解的概念,学会判断某个数值是不是一元一次方程的解.
课堂导入
对于方程4x=24,容易知道
x
=
6可以使等式成立,
对于方程
170+15x
=245,你知道
x
等于什么时,等式成立吗?我们来试一试.
x
1
2
3
4
5
6
…
…
我们知道当x=5时,170+15x的值是245,所以方程
170+15x
=
245中的未知数的值应是5.
185
200
215
230
245
260
170+15x
知识点1
新知探究
使方程左右两边相等的未知数的值叫方程的解.
求方程解的过程叫做解方程.
x=420是
方程的解吗?
方程的解
知识点1
新知探究
x=1000和
x=2000中哪一个是方程
0.52x-(1-0.52)x=80的解?
解:当x=1000时,
方程左边=0.52×1000-(1-0.52)×1000=520-480=40,
右边=80,左边≠右边,所以x=1000不是此方程的解.
当x=2000时,
方程左边=
0.52×2000-(1-0.52)×2000=1040-960=80,
右边=80,左边=右边,所以x=2000是此方程的解.
知识点1
新知探究
1.
将数值代入方程左边进行计算.
2.
将数值代入方程右边进行计算.
3.
若左边=右边,则是方程的解,反之,则不是.
判断一个数值是不是方程的解的步骤:
知识点1
新知探究
方程的解与解方程的关系
(1)
方程的解与解方程是两个不同的概念,方程的解是一个具体的数值,而解方程是求方程的解的过程;
(2)
方程的解是通过解方程求得的.
知识点1
(1)
方程的解可能有多个,也可能无解,如x=1和x=2都是方程x2-3x+2=0的解,而方程|x|=-2无解.
(2)
检验一个数是不是方程的解,不能将所给的数直接代入方程中,而是要把这个数分别代入方程的左右两边,当左边=右边时,这个数是方程的解,当左边≠右边时,这个数不是方程的解.
新知探究
跟踪训练
检验
x=2是不是方程
2x-1=1+x
的解.
解:将x=2代入方程的左边,得2×2-1
=3,
将x=2代入方程的右边,得1+2=3.
因为左边=右边,
所以
x=2是方程2x-1=1+x的解.
新知探究
随堂练习
1
x=3,x=0,x=-2,各是下列哪个方程的解?
(1)
5x+7=7-2x;
(2)
6x-8=8x-4;
(3)
3x-2=4+x.
x=0
x=-2
x=3
随堂练习
2
已知关于
x
的一元一次方程2(x-1)+3a=3的解为4,则
a
的值是(
)
A.-1
B.1
C.-2
D.-3
解析:将x=4代入2(x-1)+3a=3,
得2×3+3a=3,
解得
a=
-1.
A
根据方程的解的定义求有关字母的值时,通常先让解“回家”,即将解代入方程中,得到关于字母的方程,求解即可得到这个字母的值.
课堂小结
使方程左右两边相等的未知数的值叫方程的解.
求方程解的过程叫做解方程.
方程的解
拓展提升
1
x
=1是下列哪个方程的解(
)
A.
1-x=2
B.2x-1=4-3x
C.
D.
x-4=5x-2
B
拓展提升
2
若
x=2是关于
x的方程的解,则.
解:将x=2代入方程,得2-2a=1+3,
解得
a=-1,
所以.
0
