人教版九年级数学上册22.3实际问题与二次函数(3)课件 (共26张PPT)
文档属性
| 名称 | 人教版九年级数学上册22.3实际问题与二次函数(3)课件 (共26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-20 10:27:42 | ||
图片预览




文档简介
(共26张PPT)
人教版数学九年级上册
建立二次函数模型解决实际问题
22.3
实际问题与二次函数
3.能运用二次函数的图象与性质进行决策。
1.掌握二次函数模型的建立,会把实际问题转化为二次函数问题。
2.利用二次函数解决拱桥及运动中的有关问题。
学习目标
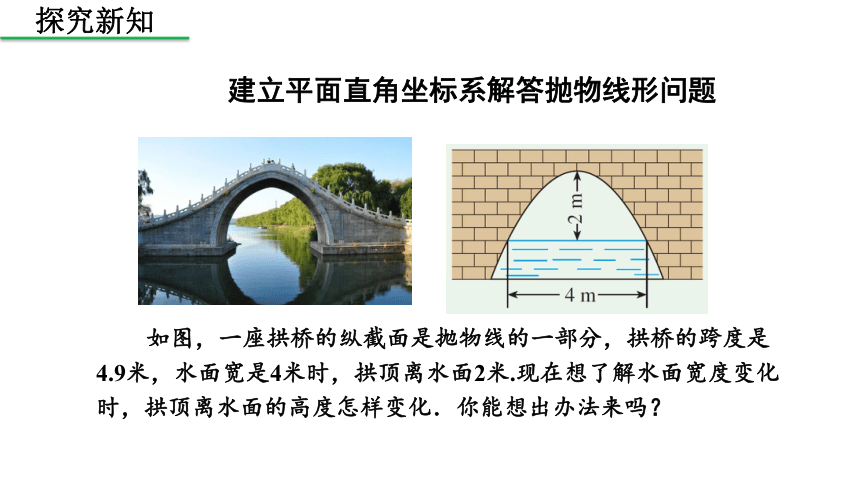
如图,一座拱桥的纵截面是抛物线的一部分,拱桥的跨度是4.9米,水面宽是4米时,拱顶离水面2米.现在想了解水面宽度变化时,拱顶离水面的高度怎样变化.你能想出办法来吗?
建立平面直角坐标系解答抛物线形问题
探究新知
建立函数模型.
这是什么样的函数呢?
拱桥的纵截面是抛物线,所以应当是个二次函数.
你能想出办法来吗?
【合作探究】
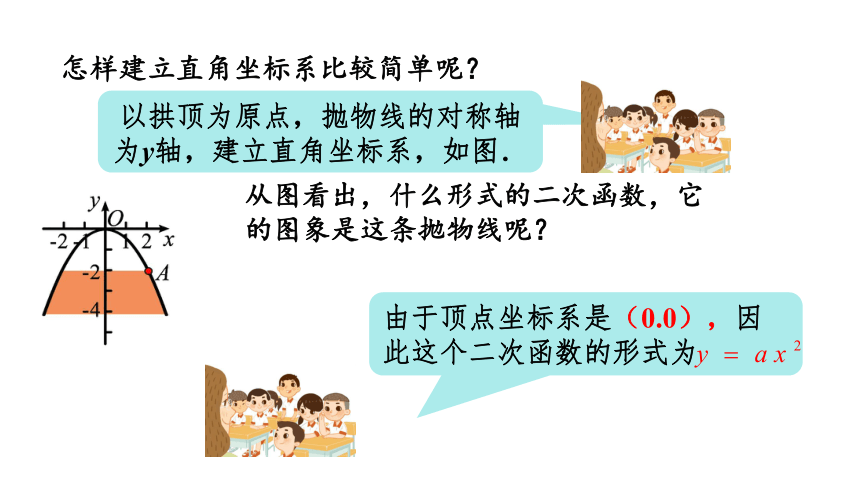
怎样建立直角坐标系比较简单呢?
以拱顶为原点,抛物线的对称轴为y轴,建立直角坐标系,如图.
从图看出,什么形式的二次函数,它的图象是这条抛物线呢?
由于顶点坐标系是(0.0),因此这个二次函数的形式为
x
O
y
-2
-4
2
1
-2
-1
A
如何确定a是多少?
已知水面宽4米时,拱顶离水面高2米,因此点A(2,-2)在抛物线上,由此得出
因此,
,其中
|x|是水面宽度的一半,y是拱顶离水面高度的相反数,这样我们就可以了解到水面宽度变化时,拱顶离水面高度怎样变化.
解得
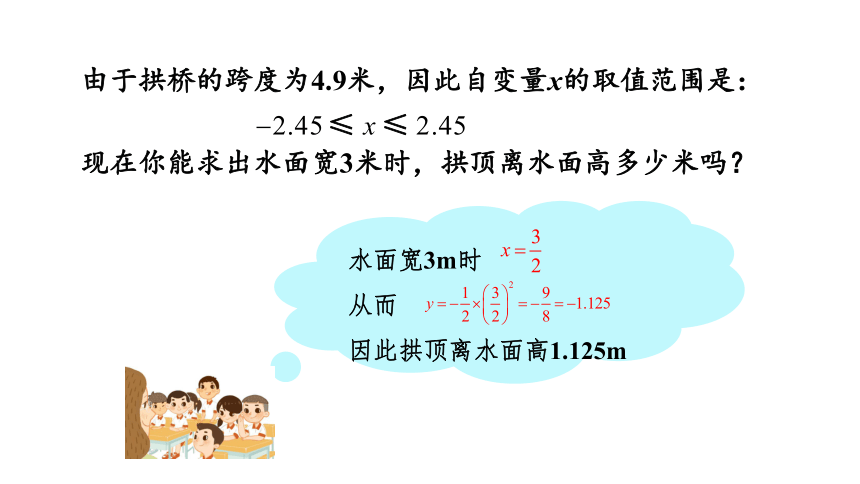
由于拱桥的跨度为4.9米,因此自变量x的取值范围是:
水面宽3m时
从而
因此拱顶离水面高1.125m
现在你能求出水面宽3米时,拱顶离水面高多少米吗?
建立二次函数模型解决实际问题的基本步骤是什么?
实际问题
建立二次函数模型
利用二次函数的图象和性质求解
实际问题的解
建立二次函数模型解决实际问题
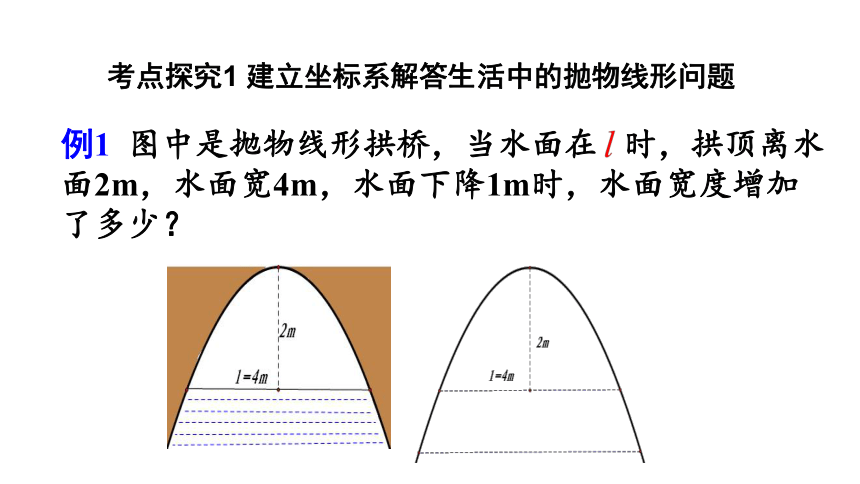
例1
图中是抛物线形拱桥,当水面在
时,拱顶离水面2m,水面宽4m,水面下降1m时,水面宽度增加了多少?
考点探究1
建立坐标系解答生活中的抛物线形问题
解法一:
如图所示以抛物线的顶点为原点,以抛物线的对称轴为y轴,建立平面直角坐标系.
∴可设这条抛物线所表示的二次函数的解析式为y=ax2
当拱桥离水面2m时,水面宽4m
即抛物线过点(2,-2)
∴这条抛物线所表示的二次函数为y=-0.5x2
.
∴-2=a×22
∴a=-0.5
当水面下降1m时,水面的纵坐标为y=-3,这时有:
因此当水面下降1m时,水面宽度增加了(2
-4
)
m.
-3=-0.5x?
解得x=±这时水面宽度为2
m
解法二:
如图所示,以抛物线和水面的两个交点的连线为x轴,以抛物线的对称轴为y轴,建立平面直角坐标系.
因此可设这条抛物线所表示的二次函数的解析式为:y=ax?+2.
此时,抛物线的顶点为(0,2)
当拱桥离水面2m时,水面宽4m
即:抛物线过点(2,0)
因此这条抛物线所表示的二次函数为:y=-0.5x?+2
当水面下降1m时,水面的纵坐标为y=-1,这时有:
因此当水面下降1m时,水面宽度增加了(2
-4)m
0=a×22+2,a=-0.5
-1=-0.5x?+2
解得x=±这时水面宽度为2
m
解法三:如图所示,以抛物线和水面的两个交点的连线为x轴,以其中的一个交点(如左边的点)为原点,建立平面直角坐标系.
因此可设这条抛物线所表示的二次函数的解析式为y=a(x-2)?+2
∵抛物线过点(0,0)
∴0=a×(-2)?+2
∴a=-0.5
因此这条抛物线所表示的二次函数为y=-0.5(x-2)
?+2.
此时,抛物线的顶点为(2,2)
当水面下降1m时,水面的纵坐标为y=-1,
这时有-1=-0.5(x-2)2+2,解得x1=2-
,
x2=2+
因此当水面下降1m时,水面宽度增加了(2-4)m.
这时水面的宽度为x-x=2,
1.理解问题;
回顾
“最大利润”和
“桥梁建筑”解决问题的过程,你能总结一下解决此类问题的基本思路吗?与同伴交流.
2.分析问题中的变量和常量,以及它们之间的关系;
3.用数学的方式表示出它们之间的关系;
4.做数学求解;
5.检验结果的合理性.
【思考】“二次函数应用”的思路
1.
有一座抛物线形拱桥,正常水位时桥下水面宽度为
20m,拱顶距离水面
4
m.如图所示的直角坐标系中,求出这条抛物线表示的函数的解析式.
O
A
C
D
B
y
x
20
m
h
解:设该拱桥形成的抛物线的解析式为y=ax2.
∵该抛物线过(10,-4),
∴-4=100a,a=-0.04
∴y=-0.04x2
.
巩固练习
例2
如图,一名运动员在距离篮球圈中心4m(水平距离)远处跳起投篮,篮球准确落入篮圈,已知篮球运行的路线为抛物线,当篮球运行水平距离为2.5m时,篮球达到最大高度,且最大高度为3.5m,如果篮圈中心距离地面3.05m,那么篮球在该运动员出手时的高度是多少米?
考点探究2
利用二次函数解决运动中抛物线形问题
探究新知
解:如图,建立直角坐标系.
则点A的坐标是(1.5,3.05),篮球在最大高度
时的位置为B(0,3.5).
以点C表示运动员投篮球的出手处.
x
y
O
设以y轴为对称轴的抛物线的解析式为
y=a(x-0)2+k
,
即y=ax2+k.而点A,B在这条抛物线上,所以有
所以该抛物线的表达式为y=0.2x2+3.5.
当
x=2.5时,y=2.25
.
故该运动员出手时的高度为2.25m.
2.25a+k=3.05,
k=3.5,
2.
一名同学推铅球,铅球出手后行进过程中离地面的高度y(单位:m)与水平距离x(单位:m)近似满足函数关系y=﹣
x2+
x+c,其图象如图所示.已知铅球落地时的水平距离为10m.
(1)求铅球出手时离地面的高度;
(2)在铅球行进过程中,当它离
地面的高度为
m时,求此时铅球
的水平距离.
巩固练习
x
y
解:(1)根据题意,将(10,0)代入y=﹣
x2+
x+c,
得
﹣×102+
×10+c=0,
解得
c=
,
即铅球出手时离地面的高度
m;
(2)将y=
代入﹣
x2+
x+
=
,
整理,得:x2﹣8x﹣9=0,
解得:x1=9,x2=﹣1(舍),
∴此时铅球的水平距离为9m.
1.
足球被从地面上踢起,它距地面的高度h(m)可用公式h=-4.9t2+19.6t来表示,其中t(s)表示足球被踢出后经过的时间,则球在
s后落地.
4
2.
如图,小李推铅球,如果铅球运行时离地面的高度y(米)关于水平距离x(米)的函数解析式为
,那么铅球运动过程中
最高点离地面的距离为
米.
x
y
O
2
课堂检测
基础题
3.
某公园草坪的防护栏是由100段形状相同的抛物线形组成的,为了牢固起见,每段护栏需要间距0.4m加设一根不锈钢的支柱,防护栏的最高点距底部0.5m(如图),则这条防护栏需要不锈钢支柱的总长度至少为(
)
A.50m
B.100m
C.160m
D.200m
C
某工厂要赶制一批抗震救灾用的大型活动板房.如图,板房一面的形状是由矩形和抛物线的一部分组成,矩形长为12m,抛物线拱高为5.6m.
(1)在如图所示的平面直角坐标系中,求抛物线的表达式.
解:(1)设抛物线的表达式为y=ax2
.
∵点B(6,﹣5.6)在抛物线的图象上,
∴﹣5.6=36a,
∴抛物线的表达式为
提升题
(2)现需在抛物线AOB的区域内安装几扇窗户,窗户的底边在AB上,每扇窗户宽1.5m,高1.6m,相邻窗户之间的间距均为0.8m,左右两边窗户的窗角所在的点到抛物线的水平距离至少为0.8m.请计算最多可安装几扇这样的窗户????????
(2)设窗户上边所在直线交抛物线于C,D两点,D点坐标为(k,t),已知窗户高1.6m,
∴t=﹣5.6﹣(﹣1.6)=﹣4
∴
????????????????,解得k=
???????????,
即k1≈5.07,k2≈﹣5.07
∴CD=5.07×2≈10.14(m)
设最多可安装n扇窗户,
∴1.5n+0.8(n﹣1)+0.8×2≤10.14,解得n≤4.06.
则最大的正整数为4.
答:最多可安装4扇窗户.
解:
悬索桥两端主塔塔顶之间的主悬钢索,其形状可近似地看作抛物线,水平桥面与主悬钢索之间用垂直钢索连接.已知两端主塔之间的水平距离为900
m,两主塔塔顶距桥面的高度为81.5
m,主悬钢索最低点离桥面的高度为0.5
m.
(1)若以桥面所在直线为x轴,抛物线的对称轴为y轴,建立平面直角坐标系,如图所示,求这条抛物线对应的函数表达式;
y
x
O
-450
450
拓展题
解:根据题意,得抛物线的顶点坐标为(0,0.5),
对称轴为y轴,设抛物线的函数表达式为y=ax2+0.5.
抛物线经过点(450,81.5),代入上式,得
81.5=a?4502+0.5.
解得
故所求表达式为
y
x
O
-450
450
(2)计算距离桥两端主塔分别为100m,50m处垂直钢索的长.
y
x
O
-450
450
解:当x=450100=350(m)时,得
当x=450﹣50=400(m)时,得
转化
回归
(二次函数的图象和性质)
拱桥问题
运动中的抛物线问题
(实物中的抛物线形问题)
建立恰当的直角坐标系
能够将实际距离准确的转化为点的坐标;
选择运算简便的方法.
实际问题
数学模型
转化的关键
总结新知
人教版数学九年级上册
建立二次函数模型解决实际问题
22.3
实际问题与二次函数
3.能运用二次函数的图象与性质进行决策。
1.掌握二次函数模型的建立,会把实际问题转化为二次函数问题。
2.利用二次函数解决拱桥及运动中的有关问题。
学习目标
如图,一座拱桥的纵截面是抛物线的一部分,拱桥的跨度是4.9米,水面宽是4米时,拱顶离水面2米.现在想了解水面宽度变化时,拱顶离水面的高度怎样变化.你能想出办法来吗?
建立平面直角坐标系解答抛物线形问题
探究新知
建立函数模型.
这是什么样的函数呢?
拱桥的纵截面是抛物线,所以应当是个二次函数.
你能想出办法来吗?
【合作探究】
怎样建立直角坐标系比较简单呢?
以拱顶为原点,抛物线的对称轴为y轴,建立直角坐标系,如图.
从图看出,什么形式的二次函数,它的图象是这条抛物线呢?
由于顶点坐标系是(0.0),因此这个二次函数的形式为
x
O
y
-2
-4
2
1
-2
-1
A
如何确定a是多少?
已知水面宽4米时,拱顶离水面高2米,因此点A(2,-2)在抛物线上,由此得出
因此,
,其中
|x|是水面宽度的一半,y是拱顶离水面高度的相反数,这样我们就可以了解到水面宽度变化时,拱顶离水面高度怎样变化.
解得
由于拱桥的跨度为4.9米,因此自变量x的取值范围是:
水面宽3m时
从而
因此拱顶离水面高1.125m
现在你能求出水面宽3米时,拱顶离水面高多少米吗?
建立二次函数模型解决实际问题的基本步骤是什么?
实际问题
建立二次函数模型
利用二次函数的图象和性质求解
实际问题的解
建立二次函数模型解决实际问题
例1
图中是抛物线形拱桥,当水面在
时,拱顶离水面2m,水面宽4m,水面下降1m时,水面宽度增加了多少?
考点探究1
建立坐标系解答生活中的抛物线形问题
解法一:
如图所示以抛物线的顶点为原点,以抛物线的对称轴为y轴,建立平面直角坐标系.
∴可设这条抛物线所表示的二次函数的解析式为y=ax2
当拱桥离水面2m时,水面宽4m
即抛物线过点(2,-2)
∴这条抛物线所表示的二次函数为y=-0.5x2
.
∴-2=a×22
∴a=-0.5
当水面下降1m时,水面的纵坐标为y=-3,这时有:
因此当水面下降1m时,水面宽度增加了(2
-4
)
m.
-3=-0.5x?
解得x=±这时水面宽度为2
m
解法二:
如图所示,以抛物线和水面的两个交点的连线为x轴,以抛物线的对称轴为y轴,建立平面直角坐标系.
因此可设这条抛物线所表示的二次函数的解析式为:y=ax?+2.
此时,抛物线的顶点为(0,2)
当拱桥离水面2m时,水面宽4m
即:抛物线过点(2,0)
因此这条抛物线所表示的二次函数为:y=-0.5x?+2
当水面下降1m时,水面的纵坐标为y=-1,这时有:
因此当水面下降1m时,水面宽度增加了(2
-4)m
0=a×22+2,a=-0.5
-1=-0.5x?+2
解得x=±这时水面宽度为2
m
解法三:如图所示,以抛物线和水面的两个交点的连线为x轴,以其中的一个交点(如左边的点)为原点,建立平面直角坐标系.
因此可设这条抛物线所表示的二次函数的解析式为y=a(x-2)?+2
∵抛物线过点(0,0)
∴0=a×(-2)?+2
∴a=-0.5
因此这条抛物线所表示的二次函数为y=-0.5(x-2)
?+2.
此时,抛物线的顶点为(2,2)
当水面下降1m时,水面的纵坐标为y=-1,
这时有-1=-0.5(x-2)2+2,解得x1=2-
,
x2=2+
因此当水面下降1m时,水面宽度增加了(2-4)m.
这时水面的宽度为x-x=2,
1.理解问题;
回顾
“最大利润”和
“桥梁建筑”解决问题的过程,你能总结一下解决此类问题的基本思路吗?与同伴交流.
2.分析问题中的变量和常量,以及它们之间的关系;
3.用数学的方式表示出它们之间的关系;
4.做数学求解;
5.检验结果的合理性.
【思考】“二次函数应用”的思路
1.
有一座抛物线形拱桥,正常水位时桥下水面宽度为
20m,拱顶距离水面
4
m.如图所示的直角坐标系中,求出这条抛物线表示的函数的解析式.
O
A
C
D
B
y
x
20
m
h
解:设该拱桥形成的抛物线的解析式为y=ax2.
∵该抛物线过(10,-4),
∴-4=100a,a=-0.04
∴y=-0.04x2
.
巩固练习
例2
如图,一名运动员在距离篮球圈中心4m(水平距离)远处跳起投篮,篮球准确落入篮圈,已知篮球运行的路线为抛物线,当篮球运行水平距离为2.5m时,篮球达到最大高度,且最大高度为3.5m,如果篮圈中心距离地面3.05m,那么篮球在该运动员出手时的高度是多少米?
考点探究2
利用二次函数解决运动中抛物线形问题
探究新知
解:如图,建立直角坐标系.
则点A的坐标是(1.5,3.05),篮球在最大高度
时的位置为B(0,3.5).
以点C表示运动员投篮球的出手处.
x
y
O
设以y轴为对称轴的抛物线的解析式为
y=a(x-0)2+k
,
即y=ax2+k.而点A,B在这条抛物线上,所以有
所以该抛物线的表达式为y=0.2x2+3.5.
当
x=2.5时,y=2.25
.
故该运动员出手时的高度为2.25m.
2.25a+k=3.05,
k=3.5,
2.
一名同学推铅球,铅球出手后行进过程中离地面的高度y(单位:m)与水平距离x(单位:m)近似满足函数关系y=﹣
x2+
x+c,其图象如图所示.已知铅球落地时的水平距离为10m.
(1)求铅球出手时离地面的高度;
(2)在铅球行进过程中,当它离
地面的高度为
m时,求此时铅球
的水平距离.
巩固练习
x
y
解:(1)根据题意,将(10,0)代入y=﹣
x2+
x+c,
得
﹣×102+
×10+c=0,
解得
c=
,
即铅球出手时离地面的高度
m;
(2)将y=
代入﹣
x2+
x+
=
,
整理,得:x2﹣8x﹣9=0,
解得:x1=9,x2=﹣1(舍),
∴此时铅球的水平距离为9m.
1.
足球被从地面上踢起,它距地面的高度h(m)可用公式h=-4.9t2+19.6t来表示,其中t(s)表示足球被踢出后经过的时间,则球在
s后落地.
4
2.
如图,小李推铅球,如果铅球运行时离地面的高度y(米)关于水平距离x(米)的函数解析式为
,那么铅球运动过程中
最高点离地面的距离为
米.
x
y
O
2
课堂检测
基础题
3.
某公园草坪的防护栏是由100段形状相同的抛物线形组成的,为了牢固起见,每段护栏需要间距0.4m加设一根不锈钢的支柱,防护栏的最高点距底部0.5m(如图),则这条防护栏需要不锈钢支柱的总长度至少为(
)
A.50m
B.100m
C.160m
D.200m
C
某工厂要赶制一批抗震救灾用的大型活动板房.如图,板房一面的形状是由矩形和抛物线的一部分组成,矩形长为12m,抛物线拱高为5.6m.
(1)在如图所示的平面直角坐标系中,求抛物线的表达式.
解:(1)设抛物线的表达式为y=ax2
.
∵点B(6,﹣5.6)在抛物线的图象上,
∴﹣5.6=36a,
∴抛物线的表达式为
提升题
(2)现需在抛物线AOB的区域内安装几扇窗户,窗户的底边在AB上,每扇窗户宽1.5m,高1.6m,相邻窗户之间的间距均为0.8m,左右两边窗户的窗角所在的点到抛物线的水平距离至少为0.8m.请计算最多可安装几扇这样的窗户????????
(2)设窗户上边所在直线交抛物线于C,D两点,D点坐标为(k,t),已知窗户高1.6m,
∴t=﹣5.6﹣(﹣1.6)=﹣4
∴
????????????????,解得k=
???????????,
即k1≈5.07,k2≈﹣5.07
∴CD=5.07×2≈10.14(m)
设最多可安装n扇窗户,
∴1.5n+0.8(n﹣1)+0.8×2≤10.14,解得n≤4.06.
则最大的正整数为4.
答:最多可安装4扇窗户.
解:
悬索桥两端主塔塔顶之间的主悬钢索,其形状可近似地看作抛物线,水平桥面与主悬钢索之间用垂直钢索连接.已知两端主塔之间的水平距离为900
m,两主塔塔顶距桥面的高度为81.5
m,主悬钢索最低点离桥面的高度为0.5
m.
(1)若以桥面所在直线为x轴,抛物线的对称轴为y轴,建立平面直角坐标系,如图所示,求这条抛物线对应的函数表达式;
y
x
O
-450
450
拓展题
解:根据题意,得抛物线的顶点坐标为(0,0.5),
对称轴为y轴,设抛物线的函数表达式为y=ax2+0.5.
抛物线经过点(450,81.5),代入上式,得
81.5=a?4502+0.5.
解得
故所求表达式为
y
x
O
-450
450
(2)计算距离桥两端主塔分别为100m,50m处垂直钢索的长.
y
x
O
-450
450
解:当x=450100=350(m)时,得
当x=450﹣50=400(m)时,得
转化
回归
(二次函数的图象和性质)
拱桥问题
运动中的抛物线问题
(实物中的抛物线形问题)
建立恰当的直角坐标系
能够将实际距离准确的转化为点的坐标;
选择运算简便的方法.
实际问题
数学模型
转化的关键
总结新知
同课章节目录
