人教版数学七年级上册3.4实际问题与一元一次方程(5)课件(25张PPT)
文档属性
| 名称 | 人教版数学七年级上册3.4实际问题与一元一次方程(5)课件(25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 202.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-20 07:16:22 | ||
图片预览






文档简介
(共25张PPT)
3.4 实际问题与一元一次方程
一元一次方程
人教版-数学-七年级上册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-拓展提升
知识回顾
在比赛积分问题中,常见的等量关系:
某个队的参赛场数=该队的胜场数+该队的负场数+该队的平场数;
某个队的总积分=该队的胜场积分+该队的负场积分+该队的平场积分.
学习目标
1.
体会分类思想和方程思想在解决问题中的作用,能够根据已知条件选择分类关键点对“电话计费问题”进行整体分析,从而得出整体选择方案.
2.
进一步深化对数学建模方法的体验,增强应用方程模型解决问题的意识和能力.
课堂导入
在现实生活中,做一件事往往有多种方案可供选择.如何选择对我们最有利的方案呢?
本节课我们将利用所学的知识,通过列方程、计算和比较,来选择最优方案.
知识点1
新知探究
下表中有两种移动电话计费方式:
免费
0.19
350
88
方式二
免费
0.25
150
58
方式一
被叫
主叫超时费/(元/
min)
主叫限定时间/
min
月使用
费/元
计费方式一
0
加超时费0.19元/
min
基本费88元
基本费58元
加超时费0.25元/
min
150
min
350
min
计费方式二
知识点1
新知探究
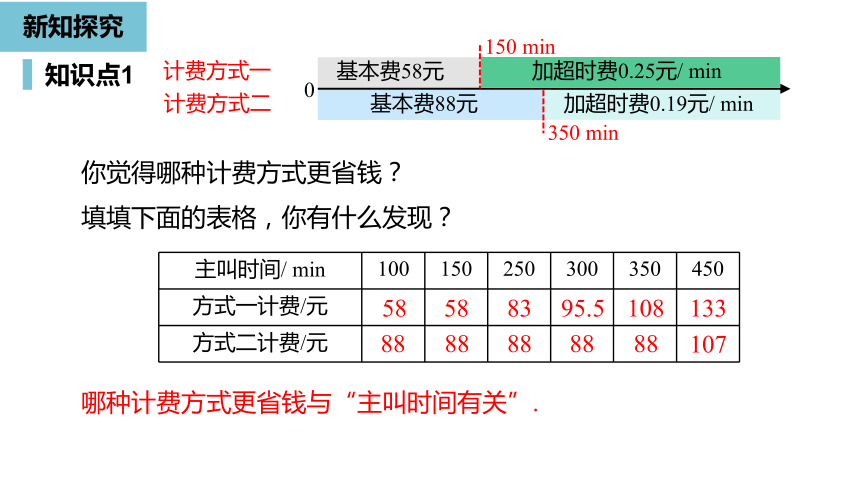
你觉得哪种计费方式更省钱?
填填下面的表格,你有什么发现?
主叫时间/
min
100
150
250
300
350
450
方式一计费/元
方式二计费/元
58
58
83
95.5
108
133
88
88
88
88
88
107
计费方式一
0
加超时费0.19元/
min
基本费88元
基本费58元
加超时费0.25元/
min
150
min
350
min
计费方式二
哪种计费方式更省钱与“主叫时间有关”.
知识点1
新知探究
考虑
t
的取值时,两个主叫限定时间
150
min和
350
min是不同时间范围的划分点.
计费时首先要看主叫是否超过限定时间,主叫不超过限定时间,月使用费一定;主叫超过限定时间,超时部分加收超时费.
设一个月内移动电话主叫为
t
min
(t是正整数),列表说明:当
t
在不同时间范围内取值时,按方式一和方式二如何计费.
知识点1
新知探究
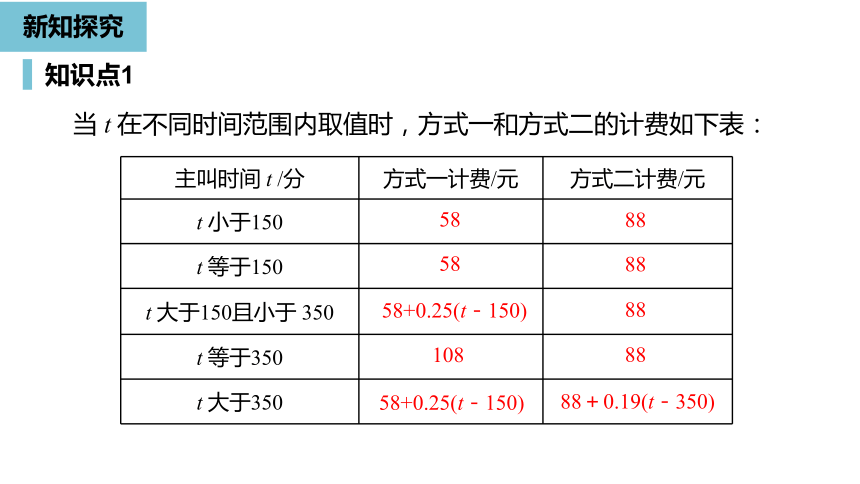
当
t
在不同时间范围内取值时,方式一和方式二的计费如下表:
主叫时间
t
/分
方式一计费/元
方式二计费/元
t
小于150
t
等于150
t
大于150且小于
350
t
等于350
t
大于350
58
88
58
88
58+0.25(t-150)
88
88
108
58+0.25(t-150)
88+0.19(t-350)
知识点1
新知探究
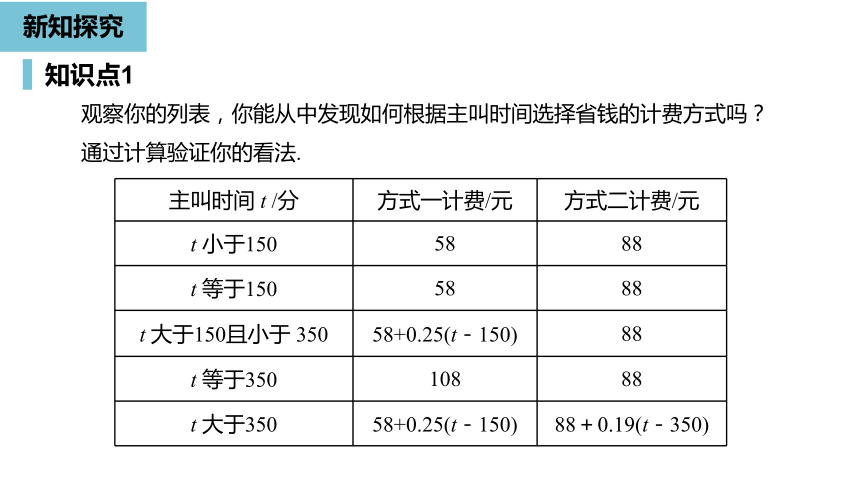
主叫时间
t
/分
方式一计费/元
方式二计费/元
t
小于150
58
88
t
等于150
58
88
t
大于150且小于
350
58+0.25(t-150)
88
t
等于350
108
88
t
大于350
58+0.25(t-150)
88+0.19(t-350)
观察你的列表,你能从中发现如何根据主叫时间选择省钱的计费方式吗?通过计算验证你的看法.
知识点1
新知探究
主叫时间
t
/分
方式一计费/元
方式二计费/元
t
小于150
58
88
t
等于150
58
88
当
t
≤150时,方式一计费少(58元);
(1)
比较下列表格的第2、3行,你能得出什么结论?
<
<
知识点1
新知探究
主叫时间
t
/分
方式一计费/元
方式二计费/元
t
等于150
58
88
t
大于150且小于
350
58+0.25(t-150)
88
t
等于350
108
88
(2)
比较下列表格的第2、4行,你能得出什么结论?
>
<
当t
大于150且小于
350时,存在某一个值,使得两种方式计费相等.
依题意
,得
58+0.25(t-150)
=
88,
解得
t
=270.
知识点1
新知探究
主叫时间
t
/分
方式一计费/元
方式二计费/元
t
大于350
58+0.25(t-150)
88+0.19(t-350)
(3)
当t
>350分时,两种计费方式哪种更合算呢?
当
t
>350时,
方式一:
58+0.25(t-150)=
108+0.25(t-350),
方式二:
88+0.19(t-350),
所以,当
t
>350时,方式二计费少.
知识点1
新知探究
综合以上的分析,可以发现:
时,选择方式一省钱;
时,选择方式二省钱;
时,方式一、方式二均可.
t
小于
270
t
大于
270
t
等于
270
解决此类问题的关键是能够根据已知条件找到合适的分段点,然后建立方程模型分类讨论,从而得出整体选择方案.
知识点1
新知探究
审题
更优惠
费用相同
列方程
用未知数表示费用
设未知数
选择最优方案问题的一般步骤:
跟踪训练
新知探究
某乳制品厂,现有鲜牛奶10吨,若直接销售,每吨可获利500元;若制成酸奶销售,相当于每吨鲜牛奶可获利1200元;若制成奶粉销售,相当于每吨鲜牛奶可获利2000元.该工厂的生产能力是:若制成酸奶,则每天可加工鲜牛奶3吨;若制成奶粉,则每天可加工鲜牛奶1吨(两种加工方式不能同时进行).受气温条件限制,这批鲜牛奶必须在4天内全部销售或加工完成.为此该厂设计了以下两种可行方案:
方案一:4天时间全部用来生产奶粉,其余鲜牛奶直接销售.
方案二:将一部分制成奶粉,其余制成酸奶,并恰好4天完成.
请你通过计算判断采用哪种方案获利更多.
跟踪训练
新知探究
解:方案一:可获利4×1×2000+(10-4)
×500=11000(元).
方案二:设制成奶粉用了
x
天,则制成酸奶用了(4-x)天.
根据题意列方程,得1×x+(4-x)×3=10.
解得
x=1.
4-x=3.
故可获利1×1×2000+3×3×1200=12800(元).
因为12800>11000,
所以采用方案二获利更多.
随堂练习
1
解:(1)
某用户5月份的用电量是200度时,
应交电费为
140×0.56+(200-140)×0.61=115(元).
为了节约能源,某市按以下规定收取每月电费:如果用电量不超过140度,每度按0.56元收费,如果超过140度,超过部分每度按0.61元收费.
(1)若某用户5月份的用电量是200度,则应交电费多少元?
(2)
若某用户4月份的电费是120元,则4月份的用电量是多少度(精确到0.1度)?
(3)
若某用户4月份平均每度的电费为0.59元,则该用户4月份应交电费多少元?
随堂练习
1
解:(2)
因为
140×0.56=78.4<120,
所以该用户4月份的用电量超过了140度.
设该用户4月份的用电量是
x
度.
则
140×0.56+(x-140)×0.61=120,解得
x≈208.2.
答:该用户4月份的用电量约是208.2度.
为了节约能源,某市按以下规定收取每月电费:如果用电量不超过140度,每度按0.56元收费,如果超过140度,超过部分每度按0.61元收费.
(1)若某用户5月份的用电量是200度,则应交电费多少元?
(2)
若某用户4月份的电费是120元,则4月份的用电量是多少度(精确到0.1度)?
(3)
若某用户4月份平均每度的电费为0.59元,则该用户4月份应交电费多少元?
随堂练习
1
解:(3)
因为0.59>
0.56,所以该用户4月份的用电量超过了140度.
设该用户4月份的用电量是
y
度,
则
140×0.56+(y-140)×0.61=0.59y,解得
y=350.
350×0.59=
206.5.
答:该用户4月份应交电费206.5元.
为了节约能源,某市按以下规定收取每月电费:如果用电量不超过140度,每度按0.56元收费,如果超过140度,超过部分每度按0.61元收费.
(1)若某用户5月份的用电量是200度,则应交电费多少元?
(2)
若某用户4月份的电费是120元,则4月份的用电量是多少度(精确到0.1度)?
(3)
若某用户4月份平均每度的电费为0.59元,则该用户4月份应交电费多少元?
随堂练习
2
某商场计划拨款9万元从厂家购进50台电视机,已知该厂家生产三种不同型号的电视机,出厂价分别是:甲种电视机每台1500元,乙种电视机每台2100元,丙种电视机每台2500元.若商场同时购进其中两种不同型号的电视机共50台,恰好用去9万元.
(1)
请你设计进货方案;
解:(1)
分三种情况讨论:
①当购进甲、乙两种型号的电视机时,
设购进甲种电视机
x
台,则购进乙种电视机(50-x)台.
根据题意列方程,得
1500x+2100(50-x)=90000,
解得
x=25.
50-x=25.
随堂练习
2
某商场计划拨款9万元从厂家购进50台电视机,已知该厂家生产三种不同型号的电视机,出厂价分别是:甲种电视机每台1500元,乙种电视机每台2100元,丙种电视机每台2500元.若商场同时购进其中两种不同型号的电视机共50台,恰好用去9万元.
(1)
请你设计进货方案;
②当购进乙、丙两种型号的电视机时,
设购进乙种电视机
y
台,则购进丙种电视机(50-y)台.
根据题意列方程,得
2100y+2500(50-y)=90000,
解得
y=87.5(不合题意,舍去).
随堂练习
2
某商场计划拨款9万元从厂家购进50台电视机,已知该厂家生产三种不同型号的电视机,出厂价分别是:甲种电视机每台1500元,乙种电视机每台2100元,丙种电视机每台2500元.若商场同时购进其中两种不同型号的电视机共50台,恰好用去9万元.
(1)
请你设计进货方案;
③当购进甲、丙两种型号的电视机时,
设购进甲种电视机
z
台,则购进丙种电视机(50-z)台.
根据题意列方程,得
1500z+2500(50-z)=90000,解得
z=35,50-z=15.
所以有以下两种方案:
方案一:购进甲、乙两种型号的电视机各25台.
方案二:购进甲种电视机35台,丙种电视机15台.
随堂练习
2
(2)若商场销售一台甲种电视机可获利150元,销售一台乙种电视机可获利200元,销售一台丙种电视机可获利250元,在同时购进两种不同型号的电视机的方案中,为使销售获利最多,则该选择哪种进货方案.
解:(2)
因为商场销售一台甲种电视机可获利150元,销售一台乙种电视机可获利200元,销售一台丙种电视机可获利250元,
所以方案一的利润为
150×25+200×25=8750(元),
方案二的利润为
150×35+250×15=9000(元).
因为8750<9000,所以选择方案二获利最多.
答:为使销售获利最多,应该选择购进甲种电视机35台,丙种电视机15台的进货方案.
课堂小结
审题
更优惠
费用相同
列方程
用未知数表示费用
设未知数
选择最优方案问题的一般步骤:
拓展提升
1
某市为更有效地利用水资源,制订了居民用水收费标准:如果一户居民每月用水量不超过15m3,每立方米按1.8元收费;如果超过15m3,超过部分按每立方米2.3元收费,其余仍按每立方米1.8元计算.另外,每立方米加收污水处理费1元.若某户居民一月份共支付水费58.5元,求该户居民一月份的用水量.
解:若该户居民一月份用水量为15m3,则需支付水费15×(1.8+1)
=42(元),
而42<58.5,故该户居民一月份用水量超过15m3.
设该户居民一月份用水量为
x
m3.
根据题意,得15×1.8+2.3(x-15)+x=58.5.解得
x=20.
答:该户居民一月份用水量为20m3.
3.4 实际问题与一元一次方程
一元一次方程
人教版-数学-七年级上册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-拓展提升
知识回顾
在比赛积分问题中,常见的等量关系:
某个队的参赛场数=该队的胜场数+该队的负场数+该队的平场数;
某个队的总积分=该队的胜场积分+该队的负场积分+该队的平场积分.
学习目标
1.
体会分类思想和方程思想在解决问题中的作用,能够根据已知条件选择分类关键点对“电话计费问题”进行整体分析,从而得出整体选择方案.
2.
进一步深化对数学建模方法的体验,增强应用方程模型解决问题的意识和能力.
课堂导入
在现实生活中,做一件事往往有多种方案可供选择.如何选择对我们最有利的方案呢?
本节课我们将利用所学的知识,通过列方程、计算和比较,来选择最优方案.
知识点1
新知探究
下表中有两种移动电话计费方式:
免费
0.19
350
88
方式二
免费
0.25
150
58
方式一
被叫
主叫超时费/(元/
min)
主叫限定时间/
min
月使用
费/元
计费方式一
0
加超时费0.19元/
min
基本费88元
基本费58元
加超时费0.25元/
min
150
min
350
min
计费方式二
知识点1
新知探究
你觉得哪种计费方式更省钱?
填填下面的表格,你有什么发现?
主叫时间/
min
100
150
250
300
350
450
方式一计费/元
方式二计费/元
58
58
83
95.5
108
133
88
88
88
88
88
107
计费方式一
0
加超时费0.19元/
min
基本费88元
基本费58元
加超时费0.25元/
min
150
min
350
min
计费方式二
哪种计费方式更省钱与“主叫时间有关”.
知识点1
新知探究
考虑
t
的取值时,两个主叫限定时间
150
min和
350
min是不同时间范围的划分点.
计费时首先要看主叫是否超过限定时间,主叫不超过限定时间,月使用费一定;主叫超过限定时间,超时部分加收超时费.
设一个月内移动电话主叫为
t
min
(t是正整数),列表说明:当
t
在不同时间范围内取值时,按方式一和方式二如何计费.
知识点1
新知探究
当
t
在不同时间范围内取值时,方式一和方式二的计费如下表:
主叫时间
t
/分
方式一计费/元
方式二计费/元
t
小于150
t
等于150
t
大于150且小于
350
t
等于350
t
大于350
58
88
58
88
58+0.25(t-150)
88
88
108
58+0.25(t-150)
88+0.19(t-350)
知识点1
新知探究
主叫时间
t
/分
方式一计费/元
方式二计费/元
t
小于150
58
88
t
等于150
58
88
t
大于150且小于
350
58+0.25(t-150)
88
t
等于350
108
88
t
大于350
58+0.25(t-150)
88+0.19(t-350)
观察你的列表,你能从中发现如何根据主叫时间选择省钱的计费方式吗?通过计算验证你的看法.
知识点1
新知探究
主叫时间
t
/分
方式一计费/元
方式二计费/元
t
小于150
58
88
t
等于150
58
88
当
t
≤150时,方式一计费少(58元);
(1)
比较下列表格的第2、3行,你能得出什么结论?
<
<
知识点1
新知探究
主叫时间
t
/分
方式一计费/元
方式二计费/元
t
等于150
58
88
t
大于150且小于
350
58+0.25(t-150)
88
t
等于350
108
88
(2)
比较下列表格的第2、4行,你能得出什么结论?
>
<
当t
大于150且小于
350时,存在某一个值,使得两种方式计费相等.
依题意
,得
58+0.25(t-150)
=
88,
解得
t
=270.
知识点1
新知探究
主叫时间
t
/分
方式一计费/元
方式二计费/元
t
大于350
58+0.25(t-150)
88+0.19(t-350)
(3)
当t
>350分时,两种计费方式哪种更合算呢?
当
t
>350时,
方式一:
58+0.25(t-150)=
108+0.25(t-350),
方式二:
88+0.19(t-350),
所以,当
t
>350时,方式二计费少.
知识点1
新知探究
综合以上的分析,可以发现:
时,选择方式一省钱;
时,选择方式二省钱;
时,方式一、方式二均可.
t
小于
270
t
大于
270
t
等于
270
解决此类问题的关键是能够根据已知条件找到合适的分段点,然后建立方程模型分类讨论,从而得出整体选择方案.
知识点1
新知探究
审题
更优惠
费用相同
列方程
用未知数表示费用
设未知数
选择最优方案问题的一般步骤:
跟踪训练
新知探究
某乳制品厂,现有鲜牛奶10吨,若直接销售,每吨可获利500元;若制成酸奶销售,相当于每吨鲜牛奶可获利1200元;若制成奶粉销售,相当于每吨鲜牛奶可获利2000元.该工厂的生产能力是:若制成酸奶,则每天可加工鲜牛奶3吨;若制成奶粉,则每天可加工鲜牛奶1吨(两种加工方式不能同时进行).受气温条件限制,这批鲜牛奶必须在4天内全部销售或加工完成.为此该厂设计了以下两种可行方案:
方案一:4天时间全部用来生产奶粉,其余鲜牛奶直接销售.
方案二:将一部分制成奶粉,其余制成酸奶,并恰好4天完成.
请你通过计算判断采用哪种方案获利更多.
跟踪训练
新知探究
解:方案一:可获利4×1×2000+(10-4)
×500=11000(元).
方案二:设制成奶粉用了
x
天,则制成酸奶用了(4-x)天.
根据题意列方程,得1×x+(4-x)×3=10.
解得
x=1.
4-x=3.
故可获利1×1×2000+3×3×1200=12800(元).
因为12800>11000,
所以采用方案二获利更多.
随堂练习
1
解:(1)
某用户5月份的用电量是200度时,
应交电费为
140×0.56+(200-140)×0.61=115(元).
为了节约能源,某市按以下规定收取每月电费:如果用电量不超过140度,每度按0.56元收费,如果超过140度,超过部分每度按0.61元收费.
(1)若某用户5月份的用电量是200度,则应交电费多少元?
(2)
若某用户4月份的电费是120元,则4月份的用电量是多少度(精确到0.1度)?
(3)
若某用户4月份平均每度的电费为0.59元,则该用户4月份应交电费多少元?
随堂练习
1
解:(2)
因为
140×0.56=78.4<120,
所以该用户4月份的用电量超过了140度.
设该用户4月份的用电量是
x
度.
则
140×0.56+(x-140)×0.61=120,解得
x≈208.2.
答:该用户4月份的用电量约是208.2度.
为了节约能源,某市按以下规定收取每月电费:如果用电量不超过140度,每度按0.56元收费,如果超过140度,超过部分每度按0.61元收费.
(1)若某用户5月份的用电量是200度,则应交电费多少元?
(2)
若某用户4月份的电费是120元,则4月份的用电量是多少度(精确到0.1度)?
(3)
若某用户4月份平均每度的电费为0.59元,则该用户4月份应交电费多少元?
随堂练习
1
解:(3)
因为0.59>
0.56,所以该用户4月份的用电量超过了140度.
设该用户4月份的用电量是
y
度,
则
140×0.56+(y-140)×0.61=0.59y,解得
y=350.
350×0.59=
206.5.
答:该用户4月份应交电费206.5元.
为了节约能源,某市按以下规定收取每月电费:如果用电量不超过140度,每度按0.56元收费,如果超过140度,超过部分每度按0.61元收费.
(1)若某用户5月份的用电量是200度,则应交电费多少元?
(2)
若某用户4月份的电费是120元,则4月份的用电量是多少度(精确到0.1度)?
(3)
若某用户4月份平均每度的电费为0.59元,则该用户4月份应交电费多少元?
随堂练习
2
某商场计划拨款9万元从厂家购进50台电视机,已知该厂家生产三种不同型号的电视机,出厂价分别是:甲种电视机每台1500元,乙种电视机每台2100元,丙种电视机每台2500元.若商场同时购进其中两种不同型号的电视机共50台,恰好用去9万元.
(1)
请你设计进货方案;
解:(1)
分三种情况讨论:
①当购进甲、乙两种型号的电视机时,
设购进甲种电视机
x
台,则购进乙种电视机(50-x)台.
根据题意列方程,得
1500x+2100(50-x)=90000,
解得
x=25.
50-x=25.
随堂练习
2
某商场计划拨款9万元从厂家购进50台电视机,已知该厂家生产三种不同型号的电视机,出厂价分别是:甲种电视机每台1500元,乙种电视机每台2100元,丙种电视机每台2500元.若商场同时购进其中两种不同型号的电视机共50台,恰好用去9万元.
(1)
请你设计进货方案;
②当购进乙、丙两种型号的电视机时,
设购进乙种电视机
y
台,则购进丙种电视机(50-y)台.
根据题意列方程,得
2100y+2500(50-y)=90000,
解得
y=87.5(不合题意,舍去).
随堂练习
2
某商场计划拨款9万元从厂家购进50台电视机,已知该厂家生产三种不同型号的电视机,出厂价分别是:甲种电视机每台1500元,乙种电视机每台2100元,丙种电视机每台2500元.若商场同时购进其中两种不同型号的电视机共50台,恰好用去9万元.
(1)
请你设计进货方案;
③当购进甲、丙两种型号的电视机时,
设购进甲种电视机
z
台,则购进丙种电视机(50-z)台.
根据题意列方程,得
1500z+2500(50-z)=90000,解得
z=35,50-z=15.
所以有以下两种方案:
方案一:购进甲、乙两种型号的电视机各25台.
方案二:购进甲种电视机35台,丙种电视机15台.
随堂练习
2
(2)若商场销售一台甲种电视机可获利150元,销售一台乙种电视机可获利200元,销售一台丙种电视机可获利250元,在同时购进两种不同型号的电视机的方案中,为使销售获利最多,则该选择哪种进货方案.
解:(2)
因为商场销售一台甲种电视机可获利150元,销售一台乙种电视机可获利200元,销售一台丙种电视机可获利250元,
所以方案一的利润为
150×25+200×25=8750(元),
方案二的利润为
150×35+250×15=9000(元).
因为8750<9000,所以选择方案二获利最多.
答:为使销售获利最多,应该选择购进甲种电视机35台,丙种电视机15台的进货方案.
课堂小结
审题
更优惠
费用相同
列方程
用未知数表示费用
设未知数
选择最优方案问题的一般步骤:
拓展提升
1
某市为更有效地利用水资源,制订了居民用水收费标准:如果一户居民每月用水量不超过15m3,每立方米按1.8元收费;如果超过15m3,超过部分按每立方米2.3元收费,其余仍按每立方米1.8元计算.另外,每立方米加收污水处理费1元.若某户居民一月份共支付水费58.5元,求该户居民一月份的用水量.
解:若该户居民一月份用水量为15m3,则需支付水费15×(1.8+1)
=42(元),
而42<58.5,故该户居民一月份用水量超过15m3.
设该户居民一月份用水量为
x
m3.
根据题意,得15×1.8+2.3(x-15)+x=58.5.解得
x=20.
答:该户居民一月份用水量为20m3.
